Monthly Archives: July 2019
Selesaikan Persamaan Nombor Indeks – Contoh 1
Solving Equation of Index Number – Example 1
Derived Quantities
1.2.2 Derived Quantities
- A derived quantity is a Physics quantity that is not a base quantity. It is the quantities which derived from the base quantities through multiplying and/or dividing them.
- For example, speed is define as rate of change of distance, Mathematically, we write this as Speed = Distance/Time. Both distance and time are base quantities, whereas speed is a derived quantity as it is derived from distance and time through division.
Example
 (Speed is derived from dividing distance by time.)
(Speed is derived from dividing distance by time.) - Belows are the derived quantities that you need to know in SPM. You need to know the equation of all the quantities, so that you can derive their unit from the equation.
- If you find it difficult to memorise all these equation, you can skip it now because you are going to learn all of them in the other chapter.













Base Quantities
1.2.1 Base Quantities
Physical Quantity
- A physical quantity is a quantity that can be measured.
- A physical quantity can be divided into base quantity and derived quantity.
Base Quantities
- Base quantities are the quantities that cannot be defined in term of other physical quantity.
- The base quantities and its units are as in the table below:
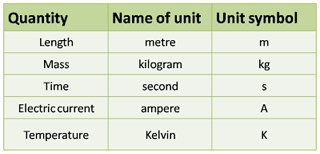 TIPS: In SPM, you MUST remember all 5 base quantities and its SI unit.
TIPS: In SPM, you MUST remember all 5 base quantities and its SI unit. Introduction to Physics
8.5.1 Alloy (Structured Questions)
Question 1:
Figure 1.1 shows the formation of bronze.
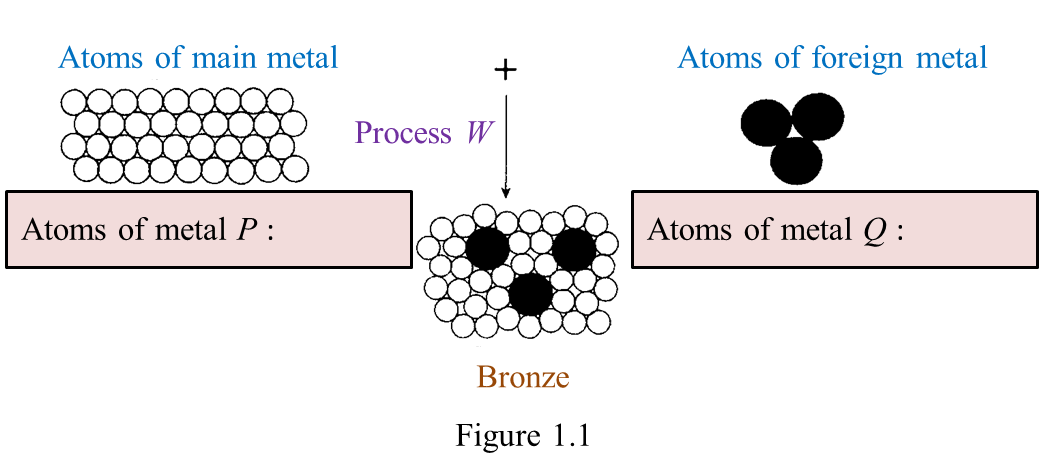
(a) On figure 1.1, name the atoms of metals, P and Q. [2 marks]
(b) Name process W. [1 mark]
(c)(i) State one property of bronze. [1 mark]
(ii) State the effect of the atoms of metal Q in bronze. [1 mark]
 (d) The medal in Figure 1.2 is made of bronze.
(d) The medal in Figure 1.2 is made of bronze.
Give one property of the medal if it is made of metal P only. [1 mark]
Answer:
(a)
P: Copper
Q: Tin
(b)
Alloying
(c)(i) Harder/ can withstand corrosion better than copper.
(c)(ii) The atoms of metal Q in bronze prevent the layers of atoms of metal W in the bronze from sliding easily over one another.
(d) Softer, more malleable, less resistant to corrosion.
Figure 1.1 shows the formation of bronze.

(a) On figure 1.1, name the atoms of metals, P and Q. [2 marks]
(b) Name process W. [1 mark]
(c)(i) State one property of bronze. [1 mark]
(ii) State the effect of the atoms of metal Q in bronze. [1 mark]
 (d) The medal in Figure 1.2 is made of bronze.
(d) The medal in Figure 1.2 is made of bronze.Give one property of the medal if it is made of metal P only. [1 mark]
Answer:
(a)
P: Copper
Q: Tin
(b)
Alloying
(c)(i) Harder/ can withstand corrosion better than copper.
(c)(ii) The atoms of metal Q in bronze prevent the layers of atoms of metal W in the bronze from sliding easily over one another.
(d) Softer, more malleable, less resistant to corrosion.
Question 2:
Diagram 2.1 shows an experiment to study the resistance of steel alloy towards corrosion.
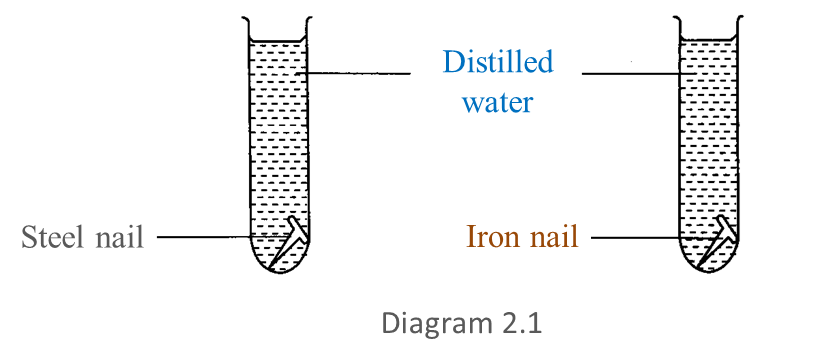
After 3 days, the result obtained is shown in Diagram 2.2.
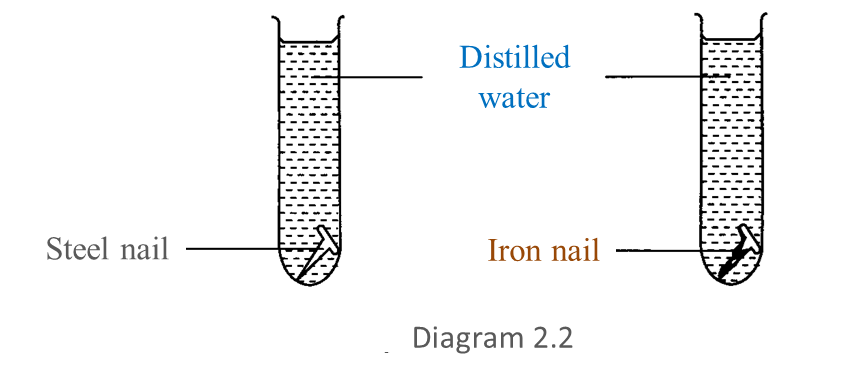
(a) Based on Diagram 2.2, write down one observation for this experiment. [1 mark]
(b) Write down one hypothesis for this experiment. [1 mark]
(c) State the variables in this experiment.
(i) Constant variable [1 mark]
(ii) Manipulated variable [1 mark]
(d) Predict the condition of the steel nail on the 5th day. [1 mark]
(e) Based on this experiment, state the operational definition for an alloy. [1 mark]
Answer:
(a) The iron nail has corroded while the steel nail has not.
(b) Steel is more resistant to corrosion than iron.
(c)(i) Distilled water, number of days the nails are immersed in water.
(any one)
(c)(ii) Type of metal (steel on iron)
(d) The steel nail will remain not corroded
(e) An alloy is a mixture of metal which is harder and more resistant to corrosion than a pure metal.
Diagram 2.1 shows an experiment to study the resistance of steel alloy towards corrosion.

After 3 days, the result obtained is shown in Diagram 2.2.

(a) Based on Diagram 2.2, write down one observation for this experiment. [1 mark]
(b) Write down one hypothesis for this experiment. [1 mark]
(c) State the variables in this experiment.
(i) Constant variable [1 mark]
(ii) Manipulated variable [1 mark]
(d) Predict the condition of the steel nail on the 5th day. [1 mark]
(e) Based on this experiment, state the operational definition for an alloy. [1 mark]
Answer:
(a) The iron nail has corroded while the steel nail has not.
(b) Steel is more resistant to corrosion than iron.
(c)(i) Distilled water, number of days the nails are immersed in water.
(any one)
(c)(ii) Type of metal (steel on iron)
(d) The steel nail will remain not corroded
(e) An alloy is a mixture of metal which is harder and more resistant to corrosion than a pure metal.