- A scalar quantity is a quantity which can be fully described by magnitude only.
- A vector quantity is a quantity which is fully described by both magnitude and direction.
Vector Diagram
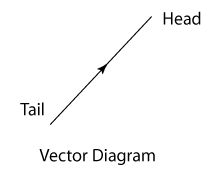
- The arrow shows the direction of the vector.
- The length representing the magnitude of the vector.
Equal Vector
Two vectors A and B may be defined to be equal if they have the same magnitude and point in the same direction.Vector Addition - Triangle Method
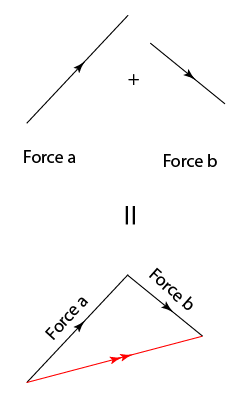
Join the tail of the 2nd vector to the head of the 1st vector. Normally the resultant vector is marked with double arrow.
Vector Addition - Parallelogram Method
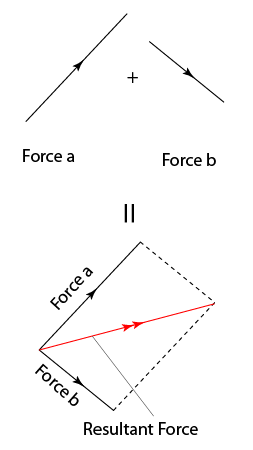
Join the tail of the 2nd vector to the tail of the 1st vector. Normally the resultant vector is marked with double arrow.
Addition of 2 Perpendicular Vectors
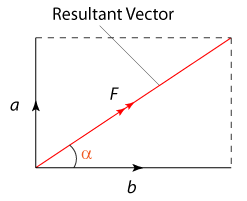
If 2 vectors (a and b) are perpendicular to each others, the magnitude and direction of the resultant vector can be determined by the following equation.
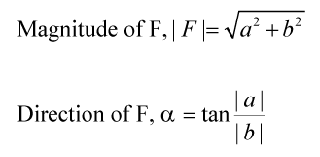
Example:
Two forces, P and Q of magnitude 10N and 12N are perpendicular to each others. What is the magnitude of the resultant force if P and Q are acting on an object?
Answer:
Magnitude of the resultant force
Two forces, P and Q of magnitude 10N and 12N are perpendicular to each others. What is the magnitude of the resultant force if P and Q are acting on an object?
Answer:
Magnitude of the resultant force
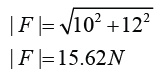
Example:
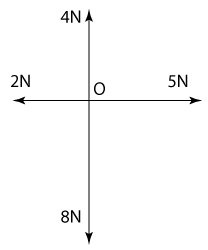
Diagram above shows that four forces of magnitude 2N, 4N, 5N and 8N are acting on point O. All the forces are perpendicular to each others. What is the magnitude of the resulatant force that acts on point O?
Answer:
The resultant force of the horizntal component = 5 - 2 = 3N to the right
The resultant force of the vertical component = 8 - 4 = 4N acting downward.
Therefore, the magtitude of these 2 force components,
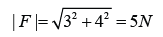

Diagram above shows that four forces of magnitude 2N, 4N, 5N and 8N are acting on point O. All the forces are perpendicular to each others. What is the magnitude of the resulatant force that acts on point O?
Answer:
The resultant force of the horizntal component = 5 - 2 = 3N to the right
The resultant force of the vertical component = 8 - 4 = 4N acting downward.
Therefore, the magtitude of these 2 force components,