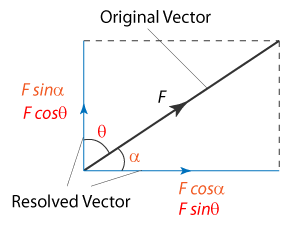
A vector can be resolve into 2 component which is perpendicular to each others.
Example:
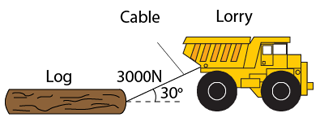
Diagram above shows a lorry pulling a log with an iron cable. If the tension of the cable is 3000N and the friction between the log and the ground is 500N, find the horizontal force that acting on the log.
Answer:
Horizontal component of the tension = 3000 cos30° =2598N
Friction = 500N
Resultant horizontal force = 2598N - 500N =2098N

Diagram above shows a lorry pulling a log with an iron cable. If the tension of the cable is 3000N and the friction between the log and the ground is 500N, find the horizontal force that acting on the log.
Answer:
Horizontal component of the tension = 3000 cos30° =2598N
Friction = 500N
Resultant horizontal force = 2598N - 500N =2098N
Example:
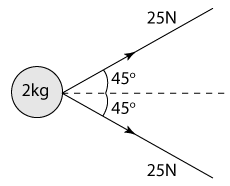
Diagram above shows two forces of magnitude 25N are acting on an object of mass 2kg. Find the acceleration of object P, in ms-2.
Answer:
Horizontal component of the forces = 25cos45° + 25cos45° = 35.36N
Vertical component of the forces = 25sin45° - 25sin45° = 0N
The acceleration of the object can be determined by the equation
F = ma
(35.36) = (2)a
a = 17.68 ms-2

Diagram above shows two forces of magnitude 25N are acting on an object of mass 2kg. Find the acceleration of object P, in ms-2.
Answer:
Horizontal component of the forces = 25cos45° + 25cos45° = 35.36N
Vertical component of the forces = 25sin45° - 25sin45° = 0N
The acceleration of the object can be determined by the equation
F = ma
(35.36) = (2)a
a = 17.68 ms-2
Inclined Plane
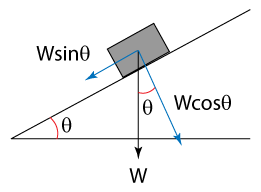
Weight component along the plane = Wsinθ.
Weight component perpendicular to the plane = Wcosθ.
Example:
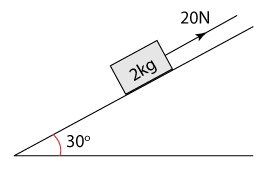
A block of mass 2 kg is pulling along a plane by a 20N force as shown in diagram above. Given that the fiction between block and the plane is 2N, find the magnitude of the resultant force parallel to the plane.
Answer:
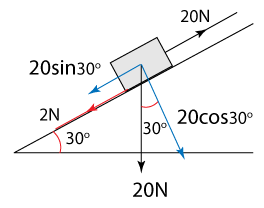
First of all, let's examine all the forces or component of forces acting along the plane.
The force pulling the block, F = 20N
The frictional force Ffric = 2N
The weight component along the plane = 20sin30° = 10N
The resultant force along the plane = 20 - 2 - 10 = 8N