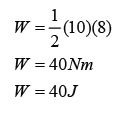- Work done by a constant force is given by the product of the force and the distance moved in the direction of the force.
- The unit of Nm(Newton metre) or J(Joule).
- Work is a scalar quantity.
Formula
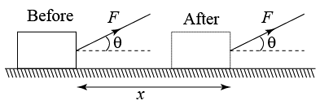

When the direction of force and motion are same, θ = 0o, therefore cosθ = 1
Work done,
Example:
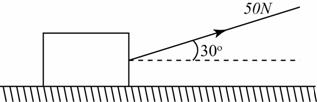
A force of 50 N acts on the block at the angle shown in the diagram. The block moves a horizontal distance of 3.0 m. Calculate the work being done by the force.
Answer
Work done,
W = F × s × cos θ
W = 50 × 3.0 × cos30o = 129.9J
Example:
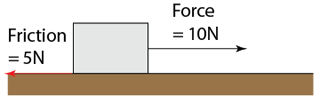
Diagram above shows a 10N force is pulling a metal. The friction between the block and the floor is 5N. If the distance travelled by the metal block is 2m, find
- the work done by the pulling force
- the work done by the frictional force
Answer:
(a) The force is in the same direction of the motion. Work done by the pulling force,
W = F × s = (10)(2) = 20J
(b) The force is not in the same direction of motion, work done by the frictional force
W = F × s × cos180°
W = (5)(2)(-1)
W = -10J
Work Done Against the Force of Gravity
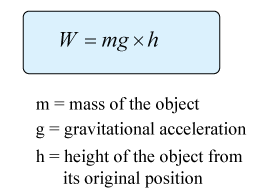
Ranjit runs up a staircase of 35 steps. Each steps is 15cm in height. Given that Ranjit's mass is 45kg, find the work done by Ranjit to reach the top of the staircase.
Answer:
In this case, Ranjit does work to overcome the gravity.
Ranjit's mass = 45kg
Vertical height of the motion, h = 35 × 0.15
Gravitational field strength, g = 10 ms-2
Work done, W = ?
W = mgh = (45)(10)(35 × 0.15) = 2362.5J
Finding Work from Force-Displacement Graph
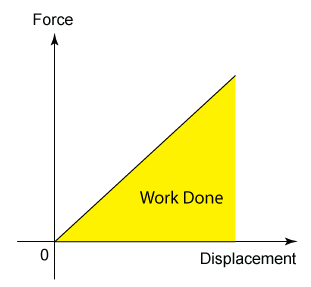
In a Force-Displacement graph, work done is equal to the area in between the graph and the horizontal axis.
Example:
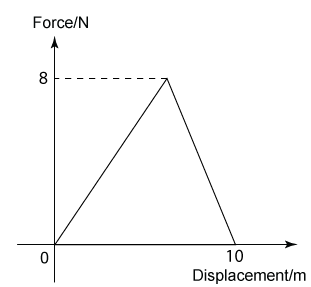
The graph above shows the force acting on a trolley of 5 kg mass over a distance of 10 m. Find the work done by the force to move the trolley.
Answer:
In a Force-Displacement graph, work done is equal to the area below the graph.
Therefore, work done