Home › SPM Physics › Forces and Pressure › 3.3.4 Measuring Atmospheric Pressure

3.3.4 Measuring Atmospheric Pressure

Posted on by
  1. Atmospheric pressure can be measured by either
    1. a simple barometer,
    2. a Fortin barometer
    3. an Aneroid barometer.
  2. In SPM, most of the questions asked are related to the simple barometer.
  3. For Fortin barometer and Aneroid barometer, you only need to know their working principle.

Simple Mercury Barometer

Fortin Barometer.
This image is created by Edal Anton Lefterov and shared under the Creative Commons Attribution-Share Alike 3.0 Unported license.



Aneroid Barometer

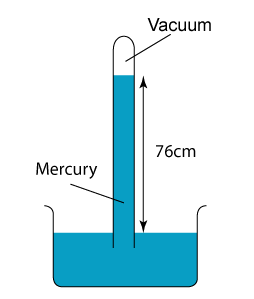
Simple Barometer

  1. Atmospheric pressure can be measured by a simple barometer.
  2. A thick glass tube (at least 1m long) is filled with mercury completely.
  3. The open end of the tube is covered with a finger and inverted in a trough of mercury.
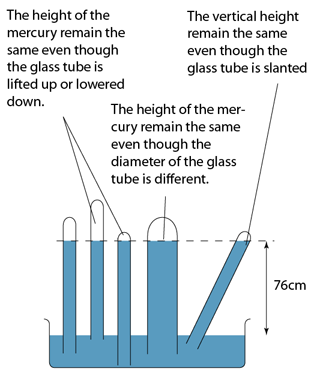
  4. The height of the mercury is proportional to the atmospheric pressure.

Using Simple Mercury Barometer


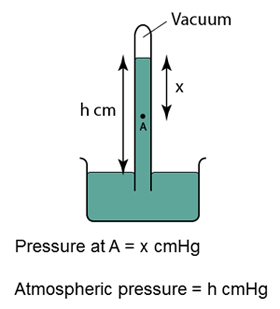
Characteristics of the Mercury Barometer



Q and A
Q: Barometer is usually made up of mercury. Explain why is it not practical to have a water barometer?

A: 
  1. The atmospheric pressure is about 10 meter water, which means it can push the water up to 10 meter height. 
  2. Therefore a water barometer must be at least 10 meter long. 
  3. This is not practical because the glass tube of the barometer may be broken or topple easily. It is also difficult to keep or move such a long tube.

Fortin Barometer

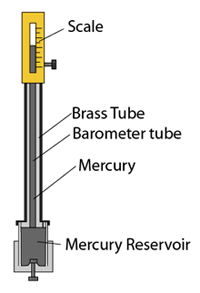
  1. The Fortin barometer is an improved version of the simple mercury barometer.
  2. The barometer tube is encased in a brass frame. This enables it to be carried around easily.
  3. Vernier scale is used for taking reading for extra accuracy.

Q & A

Q: What is the advantages of a Fortin Barometer over a Simple mercury barometer?

A:
  1. Easy to be carried around.
  2. More accurate.

Anaroid Barometer


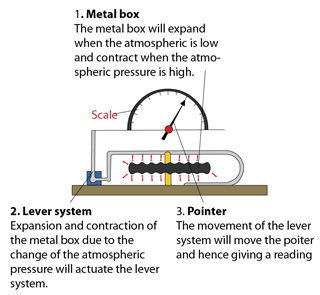
The anaroid barometer is usually used to measure altitude, which is named as altimeter.

Q & A

Q: Explain why the barometer can be used to measure altitude.

A:
The atmospheric pressure is inversely proportional to the altitude. The altitude can be determined from the atmospheric pressure.


Q & A

Q: Why a simple barometer is not suitable to be used to measure altitude?

A:
  1. Hard to be carried
  2. Mercury is volatile. It can evaporate easily
  3. Mercury is poisonous

Converting the Unit from cmHg to Pa

Pressure in unit cmHg can be converted to Pa by using the formula

P = hρg

Example 1:

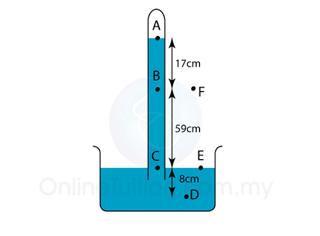
Find the pressure at point A, B, C, D, D, E and F in the unit of cmHg and Pa. [Density of mercury = 13600 kg/m³]

Answer:
Pressure in unit cmHg  Pressure in unit Pa 
PA = 0

PB = 17 cmHg

PC = 17 + 59 = 76 cmHg

PD = 76 + 8 = 84 cmHg

PE = 76 cmHg

PF = 76 cmHg		 PA = 0

PB = hρg = (0.17)(13600)(10) = 23,120 Pa

PC = hρg = (0.76)(13600)(10) = 103,360 Pa

PD = hρg = (0.84)(13600)(10) = 114,240 Pa

PE = hρg = (0.76)(13600)(10) = 103,360 Pa

PF = hρg = (0.76)(13600)(10) = 103,360 Pa


Example 2:

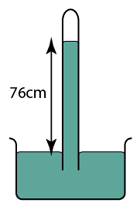
Figure above shows a simple mercury barometer. What is the value of the atmospheric pressure shown by the barometer? [Density of mercury = 13600 kg/m³]

Answer:
Atmospheric Pressure,

P = 76 cmHg

or

P = hρg = (0.76)(13600)(10) = 103360 Pa


Example 3:

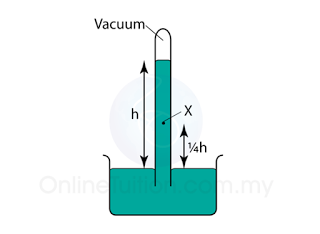
In above, the height of a mercury barometer is h when the atmospheric pressure is 101 000 Pa.
What is the pressure at X?

Answer:
Atmospheric Pressure,
Patm = h cmHg = 101 000 Pa

Pressure at X,
PX = (h - ¼h) = ¾h cmHg

PX = ¾ x 101 000 = 75 750 Pa


Example 4:

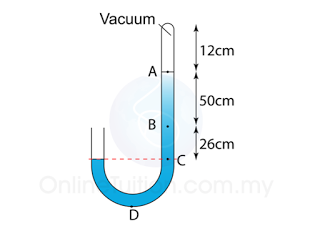
Figure above shows a mercury barometer whereby the atmospheric pressure is 760 mm Hg on a particular day. Determine the pressure at point
a. A,
b. B,
c. C.
[Density of Mercury = 13 600 kg/m³]
Answer:
a.
PA = 0

b.
PB = 50 cmHg

or

PB = hρg = (0.50)(13600)(10) = 68 000 Pa

c.
PC = 76 cmHg

or

PC = hρg = (0.76)(13600)(10) = 103 360 Pa


Example 5:

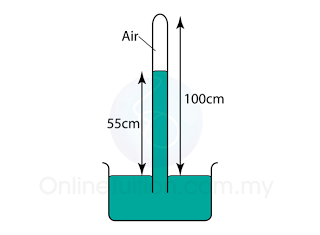
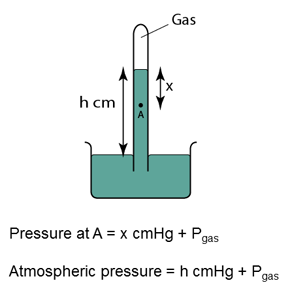
Figure above shows a simple barometer, with some air trapped in the tube. Given that the atmospheric pressure is equal to 101000 Pa, find the pressure of the trapped gas. [Density of Mercury = 13 600 kg/m³]

Answer:
Pressure of the air = Pair
Atmospheric pressure = Patm

Pair + 55 cmHg = Patm

Pair
= Patm - 55 cmHg
= 101 000 - (0.55)(13 600)(10)
= 101 000 - 74 800
= 26 200 Pa


Example 6:
If the atmospheric pressure in a housing area is 100 000 Pa, what is the magnitude of the force exerted by the atmospheric gas on a flat horizontal roof of dimensions 5m × 4m?

Answer:
Area of the roof = 5 x 4 = 20 m²

Force acted on the roof

F = PA
F = (100 000)(20)
F = 2,000,000 N


Example 7:


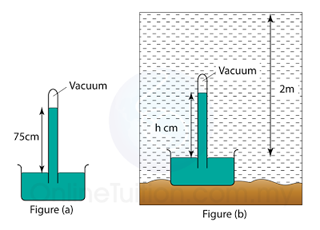
Figure(a) above shows the vertical height of mercury in a mercury barometer in a laboratory. Figure(b) shows the mercury barometer in water at a depth of 2.0 m.

Find  the vertical height (h) of the mercury in the barometer in the water. Given that the pressure at a depth of 10 m from the water surface is 75 cmHg. [Density of water = 1000 kg/m³, Density of mercury = 13 600 kg/m³]

Answer:
Atmospheric pressure,
Patm = 75 cmHg

Pressure caused by the water,
Pwater = 2/10 x 75 = 15cmHg

Pressure in 2m under water
= 75 + 15 = 90 cmHg

Vertical height of the mercury = 90cm