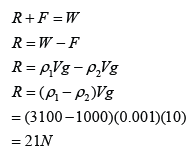Home › SPM Physics › Forces and Pressure › 3.5.2 Principle of Floatation

3.5.2 Principle of Floatation

Posted on by
  1. The principle of floatation states that when an object floats in a liquid the buoyant force/upthrust that acts on the object is equal to the weight of the object.
  2. As shown in the figure above, if the weight of the object (W) = upthrust (F), the object is in balance and therefore float on the surface of the fluid.
  3. If the weight of the object > upthrust, the object will sink into the fluid.

Note

  1. Displaced volume of fluid = volume of the object that immerse in the fluid.
  2. If weight of the object > upthrust, the object will sink into the fluid.
  3. If weight of the object = upthrust, the object is in balance and therefore float on the surface of the fluid.

In order to solve the problem related to object immerse in water, it's important to know the all forces acted on the object.

Case 1:


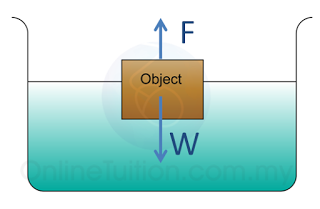
  1. The density of the object is lower than the density of the liquid. The object floats on the surface of the water.
  2. The forces acting on the object is
    1. the weight of the object(W)
    2. the upthrust (F)
Forces are in equilibrium, hence

F = W

Case 2:

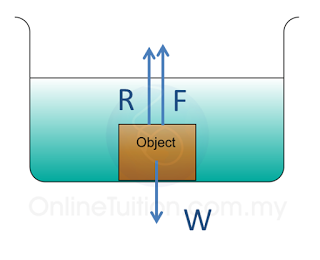
  1. The density of the object is greater than the density of the liquid. The object sink to the bottom of the water.
  2. Lying on the bottom of the water, there is a normal reaction acted on the object.
  3. The forces acting on the object is
    1. the weight of the object(W)
    2. the upthrust (F)
    3. Normal reaction (R)
Forces are in equilibrium, hence
F + R = W

Case 3:

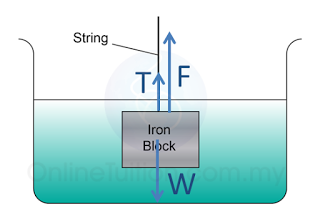
  1. The density of the object is greater than the density of the liquid. The object is hold by a string so that it does not sink deeper into the water.
  2. The forces acting on the object is
    1. the weight of the object(W)
    2. the upthrust (F)
    3. Tension of the string (T)
Forces are in equilibrium, hence
F + T = W

Case 4:

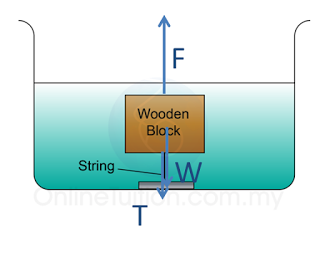
  1. The density of the object is lower than the density of the liquid. The object is hold by a string so that it does not move up to the surface of the water.
  2. The forces acting on the object is
    1. the weight of the object(W)
    2. the upthrust (F)
    3. Tension of the string (T)
Forces are in equilibrium, hence

F = W + T

Example 1:



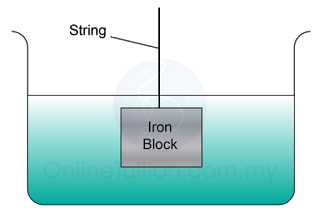
A metal block that has volume of 0.2 m³ is hanging in a water tank as shown in the figure to the left. What is the tension of the string? [ Density of the metal = 8 × 10³ kg/m³, density of water = 1 × 10³ kg/m³]

Answer:
Let,
Tension = T
Weight = W
Upthrust = F

Diagram below shows the 3 forces acted on the block.



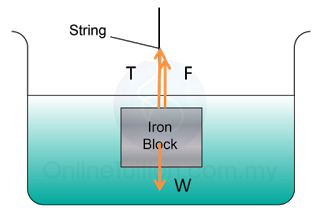
The 3 forces are in equilibrium, hence



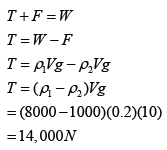
Example 2:
A wooden sphere of density 0.9 g/cm³ and mass 180 g, is anchored by a string to a lead weight at the bottom of a vessel containing water. If the wooden sphere is completely immersed in water, find the tension in the string.

Answer:
Let's draw the diagram that illustrate the situation:



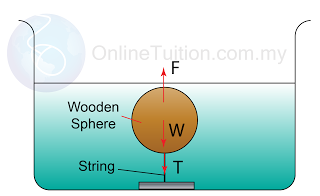
We need to determine the volume of the displaced water to find the upthrust.
Let the volume of the wooden sphere = V


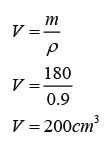
Let,
Tension = T
Weight = W
Upthrust = F

All the 3 forces are in equilibrium, hence


Example 3:



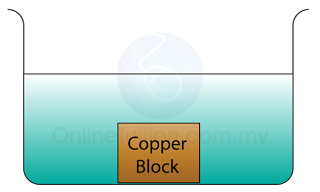
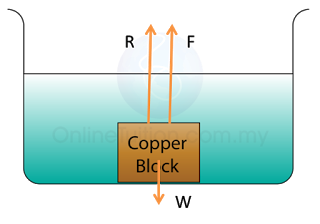
Figure above shows a copper block rest on the bottom of a vessel filled with water. Given that the volume of the block is 1000cm³. Find the normal reaction acted on the block.
[Density of water = 1000 kg/m³; Density of copper = 3100 kg/m³]

Answer:
Volume of the block, V = 1000cm³ = 0.001m³

Let,
Normal Reaction = R
Weight = W
Upthrust = F


Diagram below shows the 3 forces acted on the block.


All the 3 forces are in equilibrium, hence