- In a circuit, electromotive force is the energy per unit charge converted from the other forms of energy into electrical energy to move the charge across the whole circuit.
In equation,
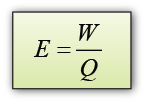
where
E = e.m.f.,
W = energy converted from non-electrical forms to electrical form
Q = positive charge.
- The unit of e.m.f. is JC-1 or V (Volt)
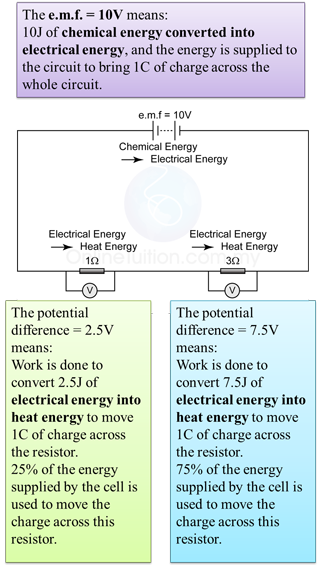
- The unit of e.m.f. is JC-1 or V (Volt). Electromotive force of 1 Volt means that 1 Joule of electrical energy is supplied to the circuit to move 1 Coulomd of charge across the whole circuit.
Electromotive Force
|
Potential Difference
|
| Similarities: Have same unit (Volt) Can be measured by Voltmeter |
|
| Definition The electromotive force (e.m.f.) is defined as the energy per unit charge that is converted from chemical, mechanical, or other forms of energy into electrical energy in a battery or dynamo. |
Definition The potential difference (p.d.) between two points is defined as the energy converted from electrical to other forms when one coulomb of positive charge passes between the two points. |
| Symbol: Denote by the symbol, E. |
Symbol: Denote by the symbol, V |
Example 1
When a 1Ω resistor is connected to the terminal of a cell, the current that flow through it is 8A. When the resistor is replaced by another resistor with resistance 4Ω, the current becomes 2⅔A. Find the
a. internal resistance of the cell
b. e.m.f. of the cell
Answer:
Experiment 1
R1 = 1Ω
I1 = 8A
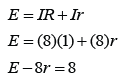
Experiment 2
R2 = 4Ω
I2 = 2⅔A

Solve the simultaneous equation
E = 12V, r = 0.5Ω
Example 2
The diagram on the left shows that the terminal potential difference of a batteries is 1.2V when a 4 Ω resistor is connected to it. The terminal potential become 1.45V when the resistor is replaced by another resistor of resistance 29Ω
Find the
a. internal resistance, r
b. e.m.f. of the batteries.
Answer:
Experiment 1
V1 = 1.2V
R1 = 4Ω
I = V/R
I = (1.2)/(4)
I = 0.3A
E = V + Ir
E = (1.2) + (0.3)r
E - 0.3r = 1.2 ------------(eq1)
Experiment 2
V2 = 1.45V
R2 = 29
I = V/R
I = (1.45)/(29)
I = 0.05A
E = V + Ir
E = (1.5) + (0.05)r
E - 0.05r = 1.45 -----------------(eq2)
Solve the simultaneous equation eq1 and eq2
E = 1.5V, r = 1Ω
The diagram on the left shows that the terminal potential difference of a batteries is 1.2V when a 4 Ω resistor is connected to it. The terminal potential become 1.45V when the resistor is replaced by another resistor of resistance 29Ω
Find the
a. internal resistance, r
b. e.m.f. of the batteries.
Answer:
Experiment 1
V1 = 1.2V
R1 = 4Ω
I = V/R
I = (1.2)/(4)
I = 0.3A
E = V + Ir
E = (1.2) + (0.3)r
E - 0.3r = 1.2 ------------(eq1)
Experiment 2
V2 = 1.45V
R2 = 29
I = V/R
I = (1.45)/(29)
I = 0.05A
E = V + Ir
E = (1.5) + (0.05)r
E - 0.05r = 1.45 -----------------(eq2)
Solve the simultaneous equation eq1 and eq2
E = 1.5V, r = 1Ω
The Linear Graph
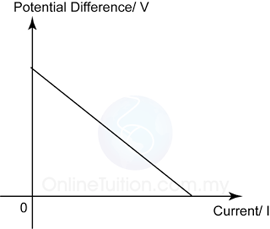
From the equation,
E = V + Ir
Therefore
V = -rI + E
Y axis = Potential difference (V)
X axis = Current (I)
Gradient od the grapf, m = - internal resistance (r)
Y intercept of the graph, c = e.m.f.
Example:
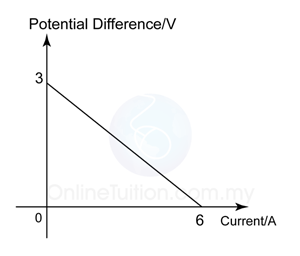
The graph shows the variation of potential difference with current of a battery.
What is the internal resistance and e.m.f. of the battery?
Answer:
e.m.f. = y-intercept = 3V
internal resistance,
r = -gradient of the graph
r = - (-3)/(6) = 0.5Ω

The graph shows the variation of potential difference with current of a battery.
What is the internal resistance and e.m.f. of the battery?
Answer:
e.m.f. = y-intercept = 3V
internal resistance,
r = -gradient of the graph
r = - (-3)/(6) = 0.5Ω