Long Question 1

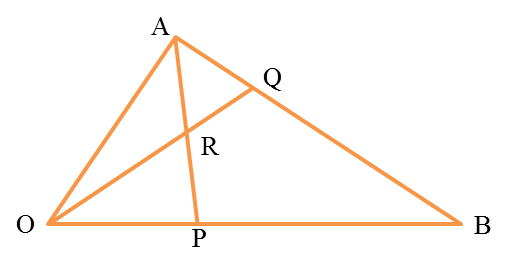
Question 1:


The above diagram shows triangle OAB. The straight line AP intersects the straight line OQ at R. It is given that $OP=\frac{1}{4}OB,AQ=\frac{1}{4}AB,\overrightarrow{OP}=4\underset{˜}{b}\text{ and }\overrightarrow{OA}=8\underset{˜}{a}.$  

(a) Express in terms of   $\underset{˜}{a}\text{ and/ or }\underset{˜}{b}:$
$\begin{array}{l}(i)\overrightarrow{AP}\\ \text{(ii)}\overrightarrow{OQ}\end{array}$

(b)(i) Given that $\overrightarrow{AR}=h\overrightarrow{AP}$ , state   $\overrightarrow{AR}$  in terms of h,    $\underset{˜}{a}\text{ and }\underset{˜}{b}\text{.}$
 (ii) Given that   $\overrightarrow{RQ}=k\overrightarrow{OQ},$ state  in terms of k,   $\underset{˜}{a}\text{ and }\underset{˜}{b}\text{.}$

(c) Using   $\overrightarrow{AQ}=\overrightarrow{AR}+\overrightarrow{RQ},$ find the value of h and of k.

Solution:
(a)(i)
$\begin{array}{l}\overrightarrow{AP}=\overrightarrow{AO}+\overrightarrow{OP}\\ \overrightarrow{AP}=-\overrightarrow{OA}+\overrightarrow{OP}\\ \overrightarrow{AP}=-8\underset{˜}{a}+4\underset{˜}{b}\end{array}$


(a)(ii)
$\begin{array}{l}\overrightarrow{OQ}=\overrightarrow{OA}+\overrightarrow{AQ}\\ \overrightarrow{OQ}=8\underset{˜}{a}+\frac{1}{4}\overrightarrow{AB}\\ \overrightarrow{OQ}=8\underset{˜}{a}+\frac{1}{4}\left(\overrightarrow{AO}+\overrightarrow{OB}\right)\\ \overrightarrow{OQ}=8\underset{˜}{a}+\frac{1}{4}\left(-8\underset{˜}{a}+4\overrightarrow{OP}\right)\\ \overrightarrow{OQ}=8\underset{˜}{a}+\frac{1}{4}\left(-8\underset{˜}{a}+4\left(4\underset{˜}{b}\right)\right)\\ \overrightarrow{OQ}=8\underset{˜}{a}-2\underset{˜}{a}+4\underset{˜}{b}\\ \overrightarrow{OQ}=6\underset{˜}{a}+4\underset{˜}{b}\end{array}$


(b)(i)
$\begin{array}{l}\overrightarrow{AR}=h\overrightarrow{AP}\\ \overrightarrow{AR}=h\left(-8\underset{˜}{a}+4\underset{˜}{b}\right)\\ \overrightarrow{AR}=-8h\underset{˜}{a}+4h\underset{˜}{b}\end{array}$


(b)(ii)
$\begin{array}{l}\overrightarrow{RQ}=k\overrightarrow{OQ}\\ \overrightarrow{RQ}=k\left(6\underset{˜}{a}+4\underset{˜}{b}\right)\\ \overrightarrow{RQ}=6k\underset{˜}{a}+4k\underset{˜}{b}\end{array}$


(c)
$\begin{array}{l}\overrightarrow{AQ}=\overrightarrow{AR}+\overrightarrow{RQ}\\ \overrightarrow{AQ}=-8h\underset{˜}{a}+4h\underset{˜}{b}+\left(6k\underset{˜}{a}+4k\underset{˜}{b}\right)\\ \overrightarrow{AO}+\overrightarrow{OQ}=-8h\underset{˜}{a}+4h\underset{˜}{b}+6k\underset{˜}{a}+4k\underset{˜}{b}\\ -8\underset{˜}{a}+6\underset{˜}{a}+4\underset{˜}{b}=-8h\underset{˜}{a}+6k\underset{˜}{a}+4h\underset{˜}{b}+4k\underset{˜}{b}\\ -2\underset{˜}{a}+4\underset{˜}{b}=-8h\underset{˜}{a}+6k\underset{˜}{a}+4h\underset{˜}{b}+4k\underset{˜}{b}\\ \\ -2=-8h+6k\\ -1=-4h+3k\to (1)\\ \\ 4=4h+4k\\ 1=h+k\\ k=1-h\to (2)\\ \\ \text{Substitute (2) into (1),}\\ -1=-4h+3\left(1-h\right)\\ -1=-4h+3-3h\\ -4=-7h\\ h=\frac{4}{7}\\ \\ \text{From (2),}\\ k=1-\frac{4}{7}=\frac{3}{7}\end{array}$