2.2 Factorisation of Quadratic Expression

2.2 Factorisation of Quadratic Expression

(A) Factorisation quadratic expressions of the form ax² + bx + c, b = 0 or c = 0

1. Factorisation of quadratic expressions is a process of finding two linear expressions whose product is the same as the quadratic expression.

2. Quadratic expressions ax² + c and ax² + bx that consist of two terms can be factorised by finding the common factors for both terms.

Example 1:

Factorise each of the following:

(a) 2x²+ 6

(b) 7p²– 3p

(c) 6x²– 9x

Solution:

(a) 2x²+ 6 = 2 (x² + 3) ← (2 is common factor)

(b) 7p²– 3p = p (7p – 3) ← (p is common factor)

(c) 6x²– 9x = 3x (2x – 3) ← (3x is common factor)

(B) Factorisation of quadratic expressions in the form ax² – c , where a and c are perfect squares

Example 2:

(a) 9p²– 16

(b) 25x²– 1

(c)

\frac{1}{4} - \frac{1}{25} x^{2}

Solution:

(a) 9p²– 16 = (3p)² – 4²= (3p – 4) (3p + 4)

(b) 25x²– 1 = (5x)² – 1²= (5x – 1) (5x + 1)

(c)

\begin{array}{l} \frac{1}{4} - \frac{1}{25} x^{2} = {(\frac{1}{2})}^{2} - {(\frac{1}{5} x)}^{2} \\ = (\frac{1}{2} - \frac{1}{5} x) (\frac{1}{2} + \frac{1}{5} x) \end{array}

(C) Factorisation quadratic expressions in the form ax² + bx + c, where a ≠ 0, b ≠ 0 and c ≠ 0

Example 3:

Factorise each of the following

(a) 3y²+ 2y – 8

(b) 4x²– 12x + 9

Solution:

(a)

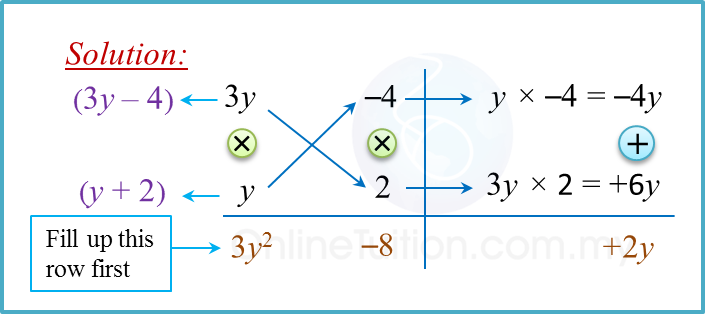
Factorise using the Cross Method

3y²+ 2y – 8 = (3y – 4) (y + 2)

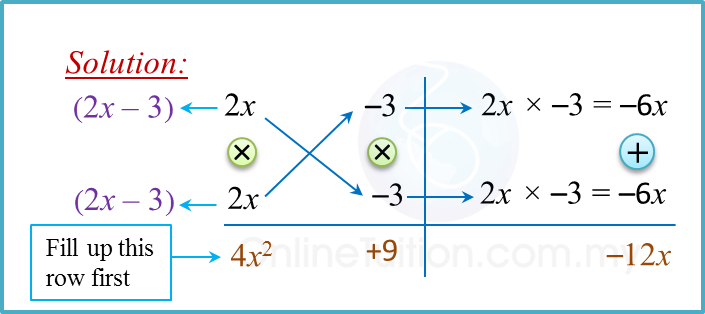
(b)

4x²– 12x + 9 = (2x – 3) (2x – 3)