5.7 SPM Practice (Long Questions 2)

Posted on April 23, 2020 by user

Question 3:

Diagram below shows a straight line JK and a straight line ST drawn on a Cartesian plane. JK is parallel to ST.

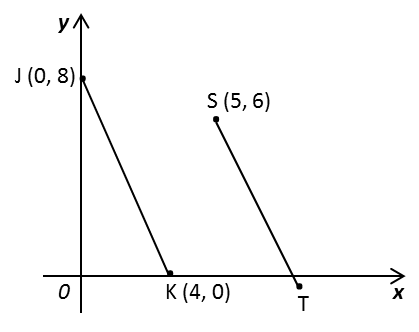
Find

(a) the equation of the straight ST,

(b) the x-intercept of the straight line ST.

Solution:

(a)
JK is parallel to ST, therefore gradient of JK = gradient of ST.

$\begin{array}{l} = \frac{8 - 0}{0 - 4} \\ = - 2 \end{array}$

Substitute m = –2 and S (5, 6) into y = mx + c

6 = –2 (5) + c

c = 16

Therefore equation of ST: y = –2x + 16

(b)
For x-intercept, y = 0

0 = –2x + 16

2x = 16

x = 8

Therefore x-intercept of ST = 8

Question 4:

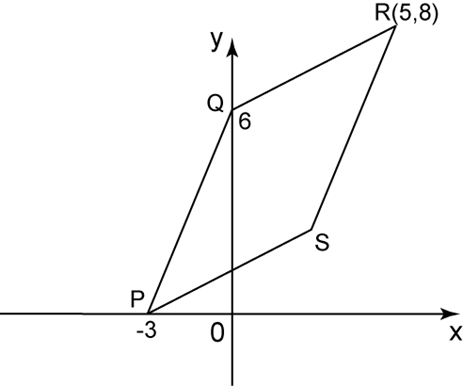
In the diagram above, PQRS is a parallelogram. Find

(a) the gradient of SR,

(b) the equation of QR,

(c) the x-intercept of QR.

Solution:

(a)
PQ is parallel to SR, gradient of PQ = gradient of SR.

$Gradient of S R = - \frac{6}{- 3} = 2$

(b)

$\begin{array}{l} Gradient of Q R = \frac{8 - 6}{5 - 0} = \frac{2}{5} \\ Substitute m = \frac{2}{5} and R (5, 8) into y = m x + c \\ 8 = \frac{2}{5} (5) + c \\ c = 6 \\ Therefore equation of Q R : y = \frac{2}{5} x + 6 \end{array}$

(c)

$\begin{array}{l} For x-intercept, y = 0 \\ 0 = \frac{2}{5} x + 6 \\ x = - 15 \end{array}$

Therefore x-intercept of QR = –15.