Question 7:
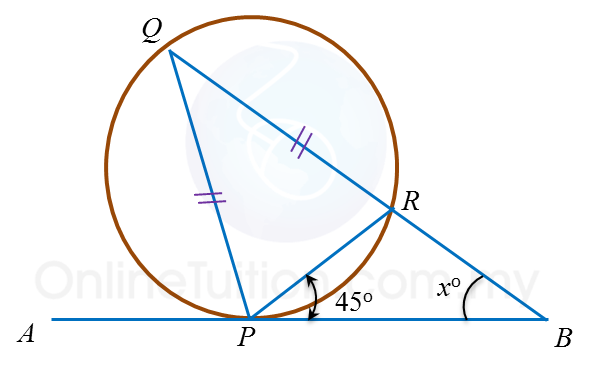

In figure above, APB is a tangent to the circle PQR at point P. QRB is a straight line. The value of x is
Solution:
∠PQR = ∠RPB = 45o
∠QPR = (180o – 45o) ÷ 2 = 67.5o
∠PQR + ∠BPQ + xo = 180o
45o + (67.5o + 45o) + xo = 180o
x = 22.5o
Question 8:
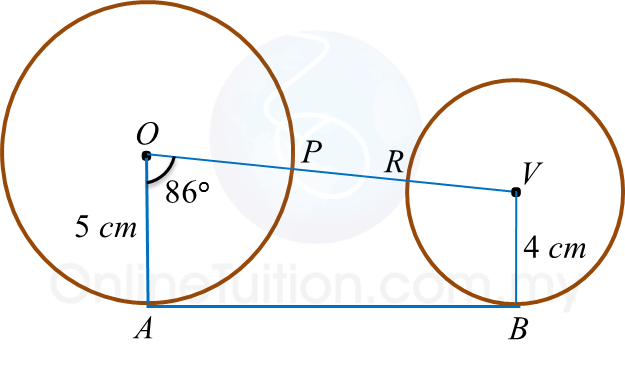
Solution:
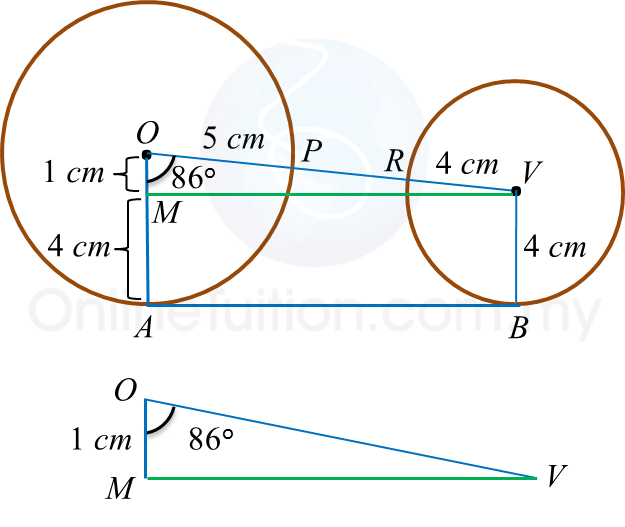

The figure above shows two circles with respective centres O and V. AB is a common tangent to the circles. OPRV is a straight line. The length, in cm, of PR is
Solution:
