Example:
6. A dot to the left of an object in a Venn diagram indicates that the object is an element of the set.
7. When a Venn diagram represents the number of elements in a set, no dot is placed to the left of the number.



List all the subsets of set P = {r, s}.
There are 2 elements, so the number of subsets of set P is 2n = 22 = 4.
Set P = {r, s}
Therefore subsets of set P = {r}, {s}, {r, s}, {}
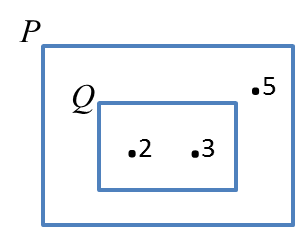
Diagram above shows a Venn diagram with the universal set, ξ = Q ∪ P. List all the subset of set P.
Set P has 3 elements, so the number of subsets of set P is 2n = 23 = 8.
Set P = {2, 3, 5}
Therefore subsets of set P = {}, {2}, {3}, {5}, {2, 3}, {2, 5}, {3, 5}, {2, 3, 5}.
It is given that the universal set, ξ = {x : 30 ≤ x < 42, x is an integer} and set P = {x : x is a number such that the sum of it its two digits is an even number}.
Find set P’.
ξ = {30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41}
P = {31, 33, 35, 37, 39, 40}
Therefore P’ = {30, 32, 34, 36, 38, 41}
Given that universal set ξ = {x : 3 < x ≤ 16, x is an integer},
Set A = {4, 11, 13, 16},
Set B = {x : x is an odd number} and
Set C = {x : x is a multiple of 3}.
The elements of the set (A ∪ C)’ ∩ B are
ξ = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}
A = {4, 11, 13, 16}
B = {5, 7, 9, 11, 13, 15}
C = {6, 9, 12, 15}
(A∪C)' = {5, 6, 7, 8, 10, 14}
Therefore (A∪C)’ ∩ B = {5, 7}
Diagram below shows a Venn diagram with the number of elements of set P, set Q and set R.
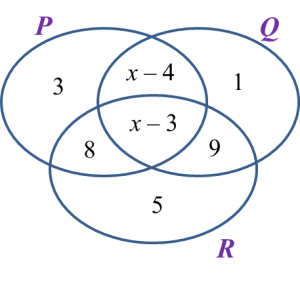
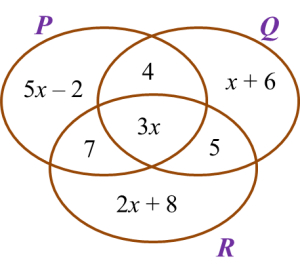
If the number of participants who participate in only one quiz is 76, find the total number of the participants.
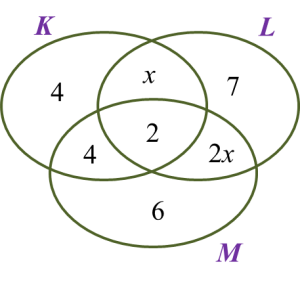
If the number of students who join both the Life Guards Club and the Martial Arts Club is 8, find the number of students who join only two clubs.
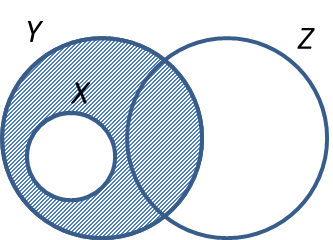
The Venn diagrams in the answer space shows sets X, Y and Z such that the universal set,
On the diagrams in the answer space, shade


The Venn diagrams in the answer space shows sets P, Q and R such that the universal set,
On the diagrams in the answer space, shade