Radians

Posted on April 21, 2020 by user

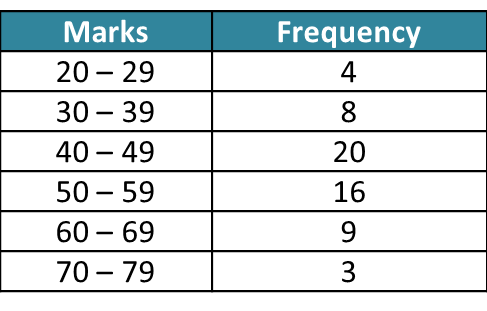
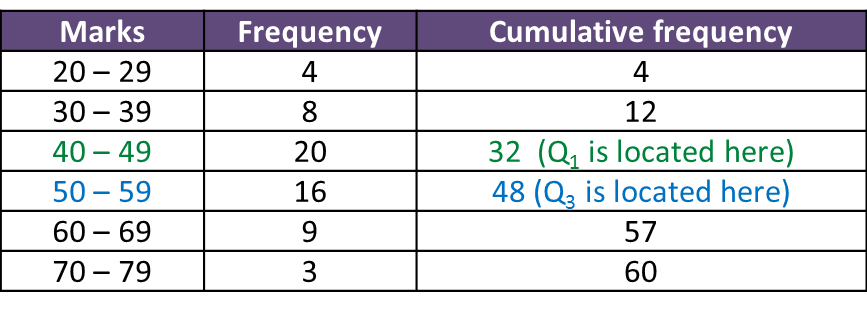
8.1 Radians
(A) Terminology:

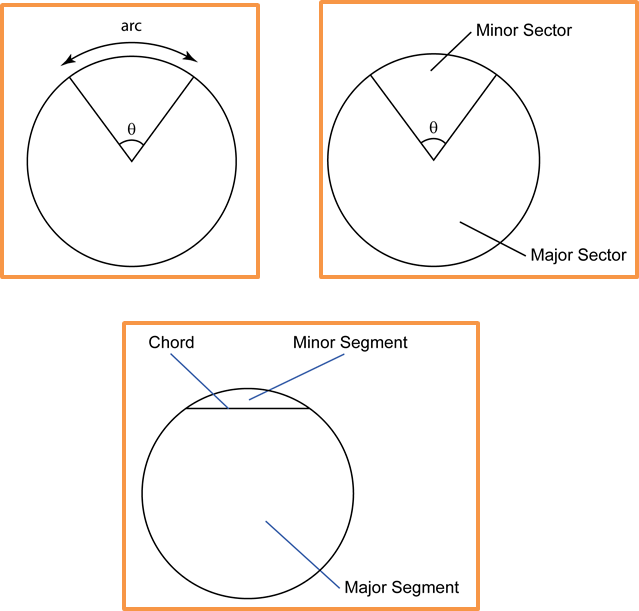
(B) Convert degrees to radians:

(C) Convert radians to degrees:

Long Questions (Question 5 & 6)

Posted on April 21, 2020 by user

Question 5:

The table shows the cumulative frequency distribution for the distance travelled by 80 children in a competition.

(a) Based on the table above, copy and complete the table below.

(b) Without drawing an ogive, estimate the interquartile range of this data.

Solution:
(a)

(b)

Interquartile range = Third Quartile – First Quartile

Third Quartile class, Q₃ = ¾ × 80 = 60

Therefore third quartile class is the class 60 – 69.

First Quartile class, Q₁= ¼ × 80 = 20

Therefore first quartile class is the class 30 – 39.

$\begin{array}{l} Interquartile Range \\ = L_{Q_{3}} + (\frac{\frac{3 N}{4} - F}{f_{_{Q_{3}}}}) c - L_{Q_{1}} + (\frac{\frac{N}{4} - F}{f_{_{Q_{1}}}}) c \\ = 59.5 + (\frac{\frac{3}{4} (80) - 59}{10}) 10 - 29.5 + (\frac{\frac{1}{4} (80) - 7}{18}) 10 \\ = 59.5 + 1 - (29.5 + 7.22) \\ = 23.78 \end{array}$

Question 6:

Table shows the daily salary obtained by 40 workers in a construction site.

Given that the median daily salary is RM35.5, find the value of x and of y.

Hence, state the modal class.

Solution:

Total workers = 40

22 + x + y = 40

x = 18 – y ------(1)

Median daily salary = 35.5

Median class is 30 – 39

$\begin{array}{l} m = L + (\frac{\frac{N}{2} - F}{f_{m}}) c \\ 35.5 = 29.5 + (\frac{\frac{40}{2} - (4 + x)}{y}) 10 \\ 6 = (\frac{16 - x}{y}) 10 \\ 6 y = 160 - 10 x \\ 3 y = 80 - 5 x - - - - (2) \end{array}$

Substitute (1) into (2):

3y = 80 – 5(18 – y)

3y = 80 – 90 + 5y

–2y = –10

y = 5

Substitute y = 5 into (1)

x = 18 – 5 = 13

Thus x = 13 and y = 5.

The modal class is 20 – 29 daily salary (RM).

Long Questions (Question 3 & 4)

Posted on April 21, 2020 by user

Question 3:

The mean of the data 1, a, 2a, 8, 9 and 15 which has been arranged in ascending order is b. If each number of the data is subtracted by 3, the new median is

$\frac{4}{7} b$ . Find

(a) The values of a and b,

(b) The variance of the new data.

Solution:
(a)

$\begin{array}{l} Mean \bar{x} = b \\ \frac{1 + a + 2 a + 8 + 9 + 15}{6} = b \\ 33 + 3 a = 6 b \\ 3 a = 6 b - 33 \\ a = 2 b - 11 ------(1) \\ New median = \frac{4 b}{7} \\ \frac{(2 a - 3) + (8 - 3)}{2} = \frac{4 b}{7} \\ \frac{2 a + 2}{2} = \frac{4 b}{7} \\ 14 a + 14 = 8 b \\ 7 a = 4 b - 7 ------(2) \\ Substitute (1) into (2), \\ 7 (2 b - 11) = 4 b - 7 \\ 14 b - 77 = 4 b - 7 \\ 10 b = 70 \\ b = 7 \\ From (1), a = 2 (7) - 11 = 3 \end{array}$

(b)

New data is (1 – 3), (3 – 3), (6 – 3), (8 – 3), (9 – 3), (15 – 3)

New data is – 2, 0, 3, 5, 6, 12

$\begin{array}{l} Variance, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2} \\ σ^{2} = \frac{{(- 2)}^{2} + {(0)}^{2} + {(3)}^{2} + {(5)}^{2} + {(6)}^{2} + {(12)}^{2}}{6} - {(\frac{- 2 + 0 + 3 + 5 + 6 + 12}{6})}^{2} \\ σ^{2} = \frac{218}{6} - 16 = 20.333 \end{array}$

Question 4:

A set of data consists of 20 numbers. The mean of the numbers is 8 and the standard deviation is 3.

(a) Calculate

$\sum x$ and

$\sum x^{2}$ .

(b) A sum of certain numbers is 72 with mean of 9 and the sum of the squares of these numbers of 800, is taken out from the set of 20 numbers. Calculate the mean and variance of the remaining numbers.

Solution:
(a)

$\begin{array}{l} Mean \bar{x} = \frac{\sum x}{N} \\ 8 = \frac{\sum x}{20} \\ \sum x = 160 \\ Standard deviation, σ = \sqrt{\frac{\sum x^{2}}{N} - {\bar{x}}^{2}} \\ 3 = \sqrt{\frac{\sum x^{2}}{N} - {\bar{x}}^{2}} \\ 9 = \frac{\sum x^{2}}{20} - 8^{2} \\ \frac{\sum x^{2}}{20} = 73 \\ \sum x^{2} = 1460 \end{array}$

(b)

$\begin{array}{l} Sum of certain numbers, M is 72 with mean of 9, \\ \frac{72}{M} = 9 \\ M = 8 \\ Mean of the remaining numbers = \frac{160 - 72}{20 - 8} = 7 \frac{1}{3} \\ Variance of the remaining numbers = \frac{1460 - 800}{12} - {(7 \frac{1}{3})}^{2} \\ = 55 - 53 \frac{7}{9} = 1 \frac{2}{9} \end{array}$

Long Questions (Question 1 & 2)

Posted on April 21, 2020 by user

Question 1:

Table shows the age of 40 tourists who visited a tourist spot.

Given that the median age is 35.5, find the value of m and of n.

Solution:

Given that the median age is 35.5, find the value of m and of n.

22 + m + n = 40

n = 18 – m -----(1)

Given median age = 35.5, therefore median class = 30 – 39

$\begin{array}{l} 35.5 = 29.5 + (\frac{20 - (4 + m)}{n}) \times 10 \\ 6 = (\frac{16 - m}{n}) \times 10 \end{array}$

6n = 160 – 10m

3n = 80 – 5m -----(2)

Substitute (1) into (2).

3 (18 – m) = 80 – 5m

54 – 3m = 80 – 5m

2m = 26

m = 13

Substitute m = 13 into (1).

n = 18 – 13

n = 5

Thus m = 13, n = 5.

Question 2:

A set of examination marks x₁, x₂, x₃, x₄, x₅, x₆ has a mean of 6 and a standard deviation of 2.4.

(a) Find

(i) the sum of the marks,

$Σ x$ ,

(ii) the sum of the squares of the marks,

$Σ x^{2}$ .

(b) Each mark is multiplied by 2 and then 3 is added to it.

Find, for the new set of marks,

(i) the mean,

(ii) the variance.

Solution:
(a)(i)

$\begin{array}{l} Given mean = 5 \\ \frac{Σ x}{6} = 6 \\ Σ x = 36 \end{array}$

(a)(ii)

$\begin{array}{l} Given σ = 2.4 \\ σ^{2} = {2.4}^{2} \\ \frac{Σ x^{2}}{n} - {\bar{X}}^{2} = 5.76 \\ \frac{Σ x^{2}}{6} - 6^{2} = 5.76 \\ \frac{Σ x^{2}}{6} = 41.76 \\ Σ x^{2} = 250.56 \end{array}$

(b)(i)

Mean of the new set of numbers

= 6(2) + 3

= 15

(b)(ii)

Variance of the original set of numbers

= 2.4²= 5.76

Variance of the new set of numbers

= 2² (5.76)

= 23.04

Short Questions (Question 10 & 11)

Posted on April 21, 2020 by user

Question 10:
A set of data consists of twelve positive numbers.

$It is given that Σ {(x - \bar{x})}^{2} = 600 and Σ x^{2} = 1032.$
Find
(a) the variance
(b) the mean

Solution:
(a)

$\begin{array}{l} Variance = \frac{Σ {(x - \bar{x})}^{2}}{N} \\ = \frac{600}{12} \\ = 50 \end{array}$

(b)

$\begin{array}{l} Variance = \frac{Σ x^{2}}{N} - {(\bar{x})}^{2} \\ 50 = \frac{1032}{12} - {(\bar{x})}^{2} \\ {(\bar{x})}^{2} = 86 - 50 \\ = 36 \\ \bar{x} = 36 \end{array}$

Question 11 (4 marks):
A set of data consists of 2, 3, 4, 5 and 6. Each number in the set is multiplied by m and added by n, where m and n are integers. It is given that the new mean is 17 and the new standard deviation is 4.242.
Find the value of m and of n.

Solution:

$\begin{array}{l} \sum x = 2 + 3 + 4 + 5 + 6 = 20 \\ \sum x^{2} = 2^{2} + 3^{2} + 4^{2} + 5^{2} + 6^{2} = 90 \\ Mean = \frac{20}{5} = 4 \\ Variance = \frac{\sum x^{2}}{n} - {(\bar{x})}^{2} \\ = \frac{90}{5} - 4^{2} = 2 \\ New mean = 17 \\ 4 m + n = 17 .......... (1) \\ New standard deviation = 4.242 \\ m \times \sqrt{2} = 4.242 \\ m = \frac{4.242}{\sqrt{2}} = 2.9995 \approx 3 \\ Substitute m = 3 into (1) : \\ 4 (3) + n = 17 \\ n = 5 \end{array}$

Short Questions (Question 5 & 6)

Posted on April 21, 2020 by user

Question 5:
A set of data consists of 9, 2, 7, x² – 1 and 4. Given the mean is 6, find
(a) the positive value of x,
(b) the median using the value of x in part (a).

Solution:
(a)

$\begin{array}{l} Mean = 6 \\ \frac{9 + 2 + 7 + x^{2} - 1 + 4}{5} = 6 \\ x^{2} + 21 = 30 \\ x^{2} = 9 \\ x = \pm 3 \\ Positive value of x = 3. \end{array}$

(b)
Arrange the numbers in ascending order
2, 4, 7, 8, 9
Median = 7

Question 6:
A set of seven numbers has a standard deviation of 3 and another set of three numbers has a standard deviation of 4. Both sets of numbers have an equal mean.
If the two sets of numbers are combined, find the variance.

Solution:

$\begin{array}{l} {\bar{X}}_{1} = \frac{Σ X_{1}}{n_{1}} \\ m = \frac{Σ X_{1}}{7} \\ Σ X_{1} = 7 m \\ m = \frac{Σ X_{2}}{3} \\ Σ X_{2} = 3 m \\ σ = \sqrt{\frac{Σ X^{2}}{N} - {(\bar{X})}^{2}} \\ σ^{2} = \frac{Σ X^{2}}{N} - {(\bar{X})}^{2} \\ 9 = \frac{Σ X_{1}^{2}}{7} - m^{2} \\ 63 = Σ X_{1}^{2} - 7 m^{2} \\ Σ X_{1}^{2} = 7 m^{2} + 63 \end{array}$

$\begin{array}{l} Similarly: \\ 16 = \frac{Σ X_{2}^{2}}{3} - m^{2} \\ 48 = Σ X_{2}^{2} - 3 m^{2} \\ Σ X_{2}^{2} = 48 + 3 m^{2} \\ Σ Y^{2} = Σ X_{1}^{2} + Σ X_{2}^{2} \\ Σ Y^{2} = 7 m^{2} + 63 + 3 m^{2} + 48 \\ = 10 m^{2} + 111 \\ Σ Y = Σ X_{1} + Σ X_{2} \\ Σ Y = 7 m + 3 m = 10 m \\ Combine Variance: \\ σ^{2} = \frac{Σ Y^{2}}{N} - {(\frac{Σ Y}{N})}^{2} \\ σ^{2} = \frac{10 m^{2} + 111}{10} - {(\frac{10 m}{10})}^{2} \\ = \frac{10 m^{2} + 111}{10} - m^{2} \\ = \frac{10 m^{2} + 111 - 10 m^{2}}{10} \\ = \frac{111}{10} = 11.1 \end{array}$

Short Questions (Question 3 & 4)

Posted on April 21, 2020 by user

Question 3:

The mean of five numbers is

$\sqrt{p}$ . The sum of the squares of the numbers is 120 and the standard deviation is 2q. Express p in terms of q.

Solution:

$\begin{array}{l} Mean \bar{x} = \frac{\sum x}{N} \\ \sqrt{p} = \frac{\sum x}{5} \\ \sum x = 5 \sqrt{p} \\ Standard deviation, σ = \sqrt{\frac{\sum x^{2}}{N} - {\bar{x}}^{2}} \\ 2 q = \sqrt{\frac{120}{5} - {(\sqrt{p})}^{2}} \\ 4 q^{2} = 24 - p \\ p = 24 - 4 q^{2} \end{array}$

Question 4:

A set of positive integers consists of 1, 4 and p. The variance for this set of integers is 6. Find the value of p.

Solution:

$\begin{array}{l} Variance, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2} \\ 6 = \frac{1^{2} + 4^{2} + p^{2}}{3} - {(\frac{1 + 4 + p}{3})}^{2} \\ 6 = \frac{17 + p^{2}}{3} - {(\frac{5 + p}{3})}^{2} \\ 6 = \frac{17 + p^{2}}{3} - [\frac{25 + 10 p + p^{2}}{9}] \\ 6 = \frac{51 + 3 p^{2} - 25 - 10 p - p^{2}}{9} \\ 2 p^{2} - 10 p + 26 = 54 \\ 2 p^{2} - 10 p + 28 = 0 \\ p^{2} - 5 p + 14 = 0 \\ (p - 7) (p + 2) = 0 \\ p = - 2 (not accepted) \\ ∴ p = 7 \end{array}$

Short Questions (Question 1 & 2)

Posted on April 21, 2020 by user

Question 1:

Given that the standard deviation of five numbers is 6 and the sum of the squares of these five numbers is 260. Find the mean of this set of numbers.

Solution:

$\begin{array}{l} Given that σ = 6, Σ x^{2} = 260. \\ σ = 6 \\ \sqrt{\frac{Σ x^{2}}{n} - {\bar{X}}^{2}} = 6 \\ \frac{Σ x^{2}}{n} - {\bar{X}}^{2} = 36 \\ \frac{260}{5} - {\bar{X}}^{2} = 36 \\ {\bar{X}}^{2} = 16 \\ \bar{X} = \pm 4 \\ ∴ mean = \pm 4 \end{array}$

Question 2:
Both of the mean and the standard deviation of 1, 3, 7, 15, m and n are 6. Find

(a) the value of m + n,

(b) the possible values of n.

Solution:

(a)

$\begin{array}{l} Given mean = 6 \\ \frac{Σ x}{n} = 6 \\ \frac{Σ x}{6} = 6 \end{array}$
1 + 3 + 7 + 15 + m + n= 36

26 + m + n= 36

m + n = 10

(b)

$\begin{array}{l} σ = 6 \\ σ^{2} = 36 \\ \frac{Σ x^{2}}{n} - {\bar{X}}^{2} = 36 \\ \frac{1 + 9 + 49 + 225 + m^{2} + n^{2}}{6} - 6^{2} = 36 \\ \frac{284 + m^{2} + n^{2}}{6} - 36 = 36 \\ \frac{284 + m^{2} + n^{2}}{6} = 72 \\ 284 + m^{2} + n^{2} = 432 \\ m^{2} + n^{2} = 148 \\ From (a), m = 10 - n \\ {(10 - n)}^{2} + n^{2} = 148 \\ 100 - 20 n + n^{2} + n^{2} = 148 \\ 2 n^{2} - 20 n - 48 = 0 \\ n^{2} - 10 n - 24 = 0 \\ (n - 6) (n + 4) = 0 \\ n = 6 or - 4 \end{array}$

Measures of Dispersion (Part 3)

Posted on April 21, 2020 by user

Measures of Dispersion (Part 3)
7.3 Variance and Standard Deviation

1. The variance is a measure of the mean for the square of the deviations from the mean.

2. The standard deviation refers to the square root for the variance.

(A) Ungrouped Data

Example 1:

Find the variance and standard deviation of the following data.

15, 17, 21, 24 and 31

Solution:

$\begin{array}{l} Variance, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2} \\ σ^{2} = \frac{15^{2} + 17^{2} + 21^{2} + 24^{2} + 31^{2}}{5} \\ - {(\frac{15 + 17 + 21 + 24 + 31}{5})}^{2} \\ σ^{2} = \frac{2492}{5} - {21.6}^{2} \\ σ^{2} = 31.84 \\ Standard deviation, σ = \sqrt{variance} \\ σ = \sqrt{31.84} \\ σ = 5.642 \end{array}$

(B) Grouped Data (without Class Interval)

Example 2:

The data below shows the numbers of children of 30 families:

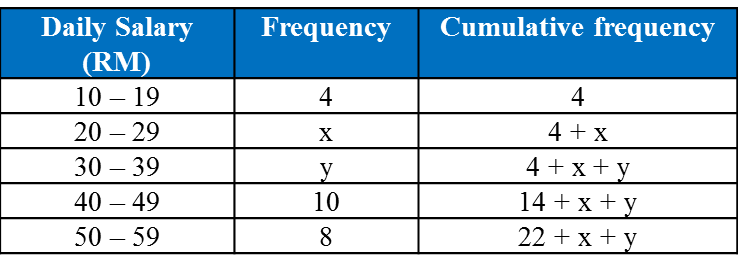
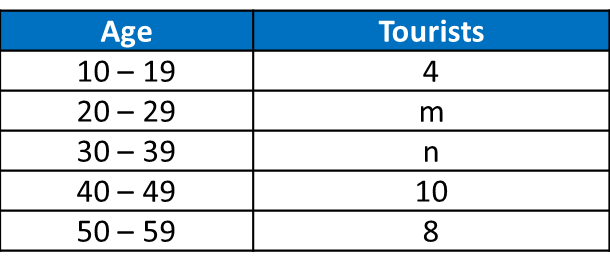
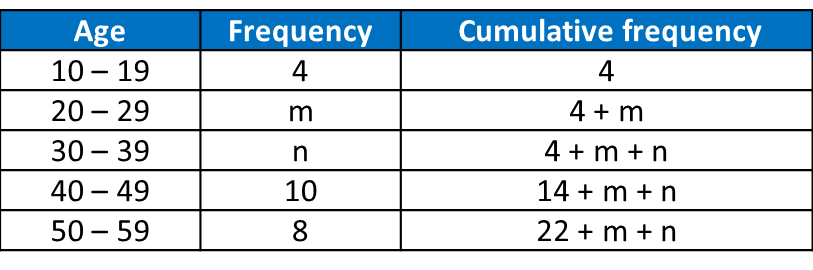
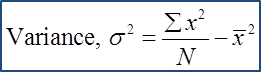
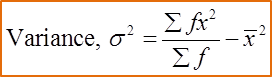
Number of child	2	3	4	5	6	7	8
Frequency	6	8	5	3	3	3	2

Find the variance and standard deviation of the data.

Solution:

$\begin{array}{l} Mean \bar{x} = \frac{\sum f x}{\sum f} \\ = \frac{(6) (2) + (8) (3) + (5) (4) + (3) (5) + (3) (6) + (3) (7) + (2) (8)}{6 + 8 + 5 + 3 + 3 + 3 + 2} \\ = \frac{126}{30} = 4.2 \\ \frac{\sum f x^{2}}{\sum f} \\ = \frac{(6) {(2)}^{2} + (8) {(3)}^{2} + (5) {(4)}^{2} + (3) {(5)}^{2} + (3) {(6)}^{2} + (3) {(7)}^{2} + (2) {(8)}^{2}}{6 + 8 + 5 + 3 + 3 + 3 + 2} \\ = \frac{634}{30} = 21.13 \\ Variance, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2} \\ σ^{2} = 21.133 - {4.2}^{2} \\ σ^{2} = 3.493 \\ Standard deviation, σ = \sqrt{variance} \\ σ = \sqrt{3.493} \\ σ = 1 .869 \end{array}$

(C) Grouped Data (with Class Interval)

Example 3:

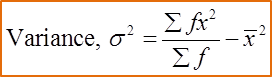
Daily Salary(RM)	Number of workers
10 – 14	40
15 – 19	25
20 – 24	15
25 – 29	12
30 – 34	8

Find the mean of daily salary and its standard deviation.

Solution:

Daily Salary (RM)	Number of workers, f	Midpoint, x	fx	fx²
10 – 14	40	12	480	5760
15 – 19	25	17	425	7225
20 – 24	15	22	330	7260
25 – 29	12	27	324	8748
30 – 34	8	32	256	8192
Total	100		1815	37185

$\begin{array}{l} Mean \bar{x} = \frac{\sum f x}{\sum f} \\ Mean of daily salary = \frac{1815}{100} = 18.15 \\ Variance, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2} \\ Standard deviation, σ = \sqrt{variance} \\ σ^{2} = \frac{37185}{100} - {18.15}^{2} \\ σ^{2} = 42.43 \\ σ = \sqrt{42.43} \\ σ = 6 .514 \end{array}$

Measures of Dispersion (Part 2)

Posted on April 21, 2020 by user

Measures of Dispersion (Part 2)
7.2b Interquartile Range 2

(C) Interquartile Range of Grouped Data (with Class Interval)

The interquartile range of grouped data can be determined by Method 1 (using a cumulative frequency table) or Method 2 (using an ogive).

Example:
The table below shows the marks obtained by a group of Form 4 students in school mathematics test.

Estimate the interquartile range.

Solution:

Method 1: From Cumulative Frequency Table

Step 1:

Lower quartile, Q₁= the

$\frac{1}{4} {(60)}^{th}$ observation

= the 15^thobservation

Upper quartile, Q₃= the

$\frac{3}{4} {(60)}^{th}$ observation
= the 45^thobservation

Step 2:

$\begin{array}{l} Lower quartile, Q_{1} = L_{1} + (\frac{\frac{1}{4} N - F_{1}}{f_{Q_{1}}}) C \\ = 39.5 + (\frac{15 - 12}{20}) 10 \\ = 39.5 + 1.5 \\ = 41 \end{array}$

Step 3:

$\begin{array}{l} Upper quartile, Q_{3} = L_{3} + (\frac{\frac{3}{4} N - F_{3}}{f_{Q_{3}}}) C \\ = 49.5 + (\frac{45 - 32}{16}) 10 \\ = 49.5 + 8.125 \\ = 57.625 \end{array}$

Step 4:

Interquartile Range

= upper quartile – lower quartile

= Q₃– Q₁

= 57.625 – 41

= 16.625