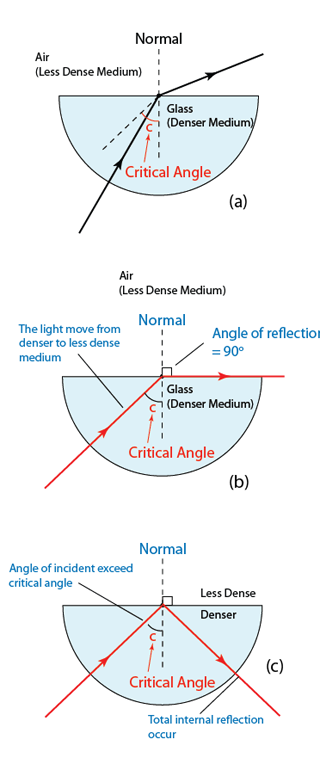
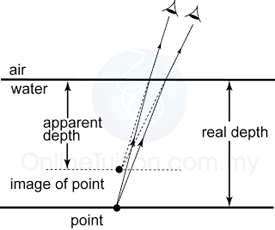
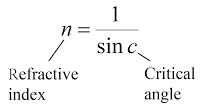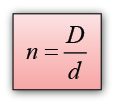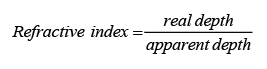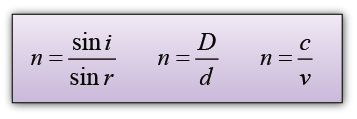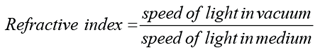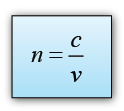- The power of a lens is defined as the reciprocal of the focal length in unit meter.
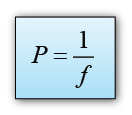
- Important Note: f is in meter
- The unit of power is diopter (D).
- The relationship of the power with the thickness and types of lens are shown in the diagram below.
Lens
|
Power of the Lens
|
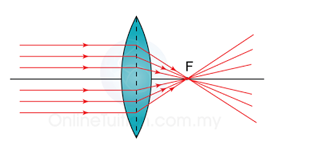
| Converging (Convex) | Positive |
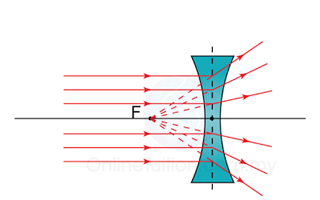
| Diverging (Concave) | Negative |
| Thick, with short focal length. | High |
| Thin, with long focal length. | Low |
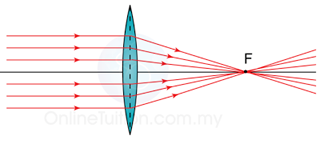
Thinner – Lower Power – Longer Focal Length
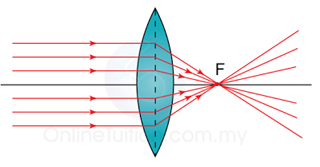
Thicker – Higher Power – Shorter Focal Length
Example:
The power of a lens is labeled as +5D. What is the focal length of the lens (in cm)? Is this a concave lens or a convex lens?
Answer:
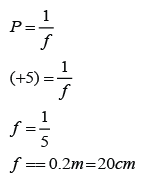
The power of the lens is positive. This is a convex lens.