Question 4 (6 marks):
Diagram shows the front view of a part of a roller coaster track in a miniature park.
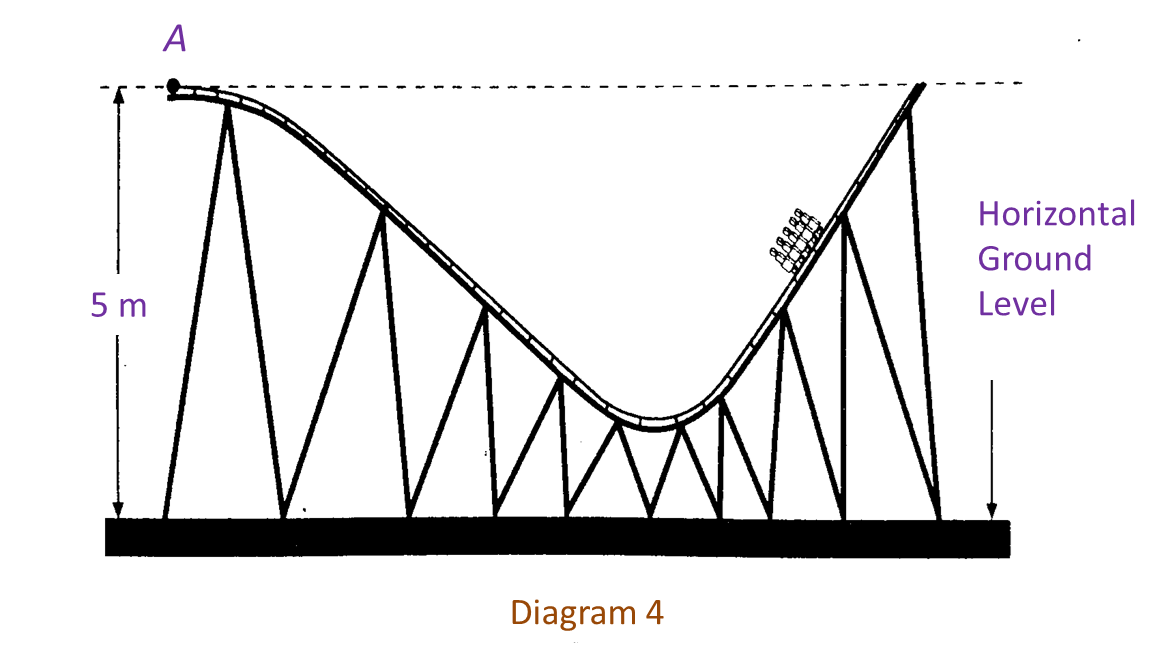
The curve part of the track of the roller coaster is represented by an equation y=164x3−316x2 , with point A as the region.
Find the shortest vertical distance, in m, from the track to ground level.
Solution:
y=164x3−316x2 ............... (1)dydx=3(164)x2−2(316)x1=364x2−38xAt turning point, dydx=0364x2−38x=0x(364x−38)=0x=0 or364x−38=0364x=38x=38×643x=8Substitute values of x into equation (1):When x=0,y=164(0)3−316(0)2y=0When x=8,y=164(8)3−316(8)2y=−4Thus, turning points : (0, 0) and (8,−4)
dydx=364x2−38xd2ydx2=2(364)x−38 =332x−38When x=0,d2ydx2=332(0)−38 =−38(<0)(0, 0) is maximum point.When x=8,d2ydx2=332(8)−38 =38(>0)(8,−4) is minimum point.Shortest vertical distance between track and ground level is at the minimum point.Shortest vertical distance=5−4=1 m
Diagram shows the front view of a part of a roller coaster track in a miniature park.

The curve part of the track of the roller coaster is represented by an equation y=164x3−316x2 , with point A as the region.
Find the shortest vertical distance, in m, from the track to ground level.
Solution:
y=164x3−316x2 ............... (1)dydx=3(164)x2−2(316)x1=364x2−38xAt turning point, dydx=0364x2−38x=0x(364x−38)=0x=0 or364x−38=0364x=38x=38×643x=8Substitute values of x into equation (1):When x=0,y=164(0)3−316(0)2y=0When x=8,y=164(8)3−316(8)2y=−4Thus, turning points : (0, 0) and (8,−4)
dydx=364x2−38xd2ydx2=2(364)x−38 =332x−38When x=0,d2ydx2=332(0)−38 =−38(<0)(0, 0) is maximum point.When x=8,d2ydx2=332(8)−38 =38(>0)(8,−4) is minimum point.Shortest vertical distance between track and ground level is at the minimum point.Shortest vertical distance=5−4=1 m