Soalan 10 (12 markah):
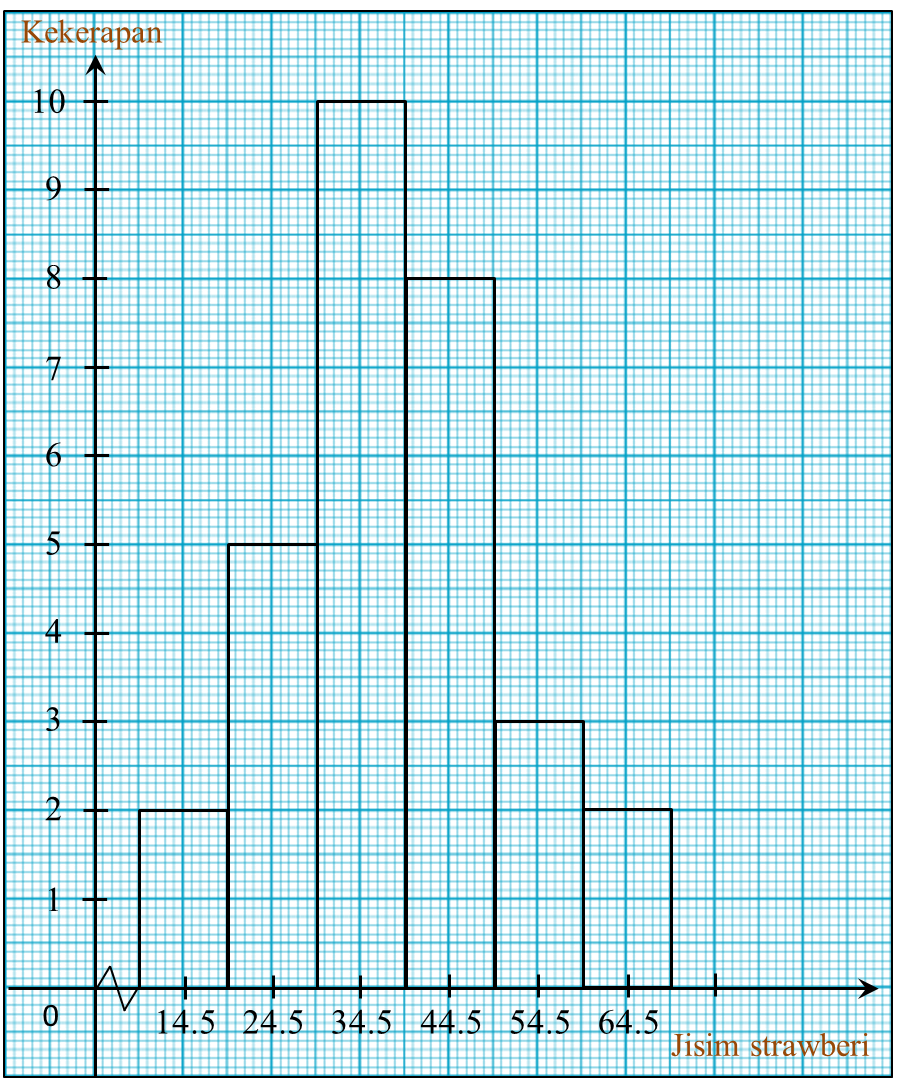
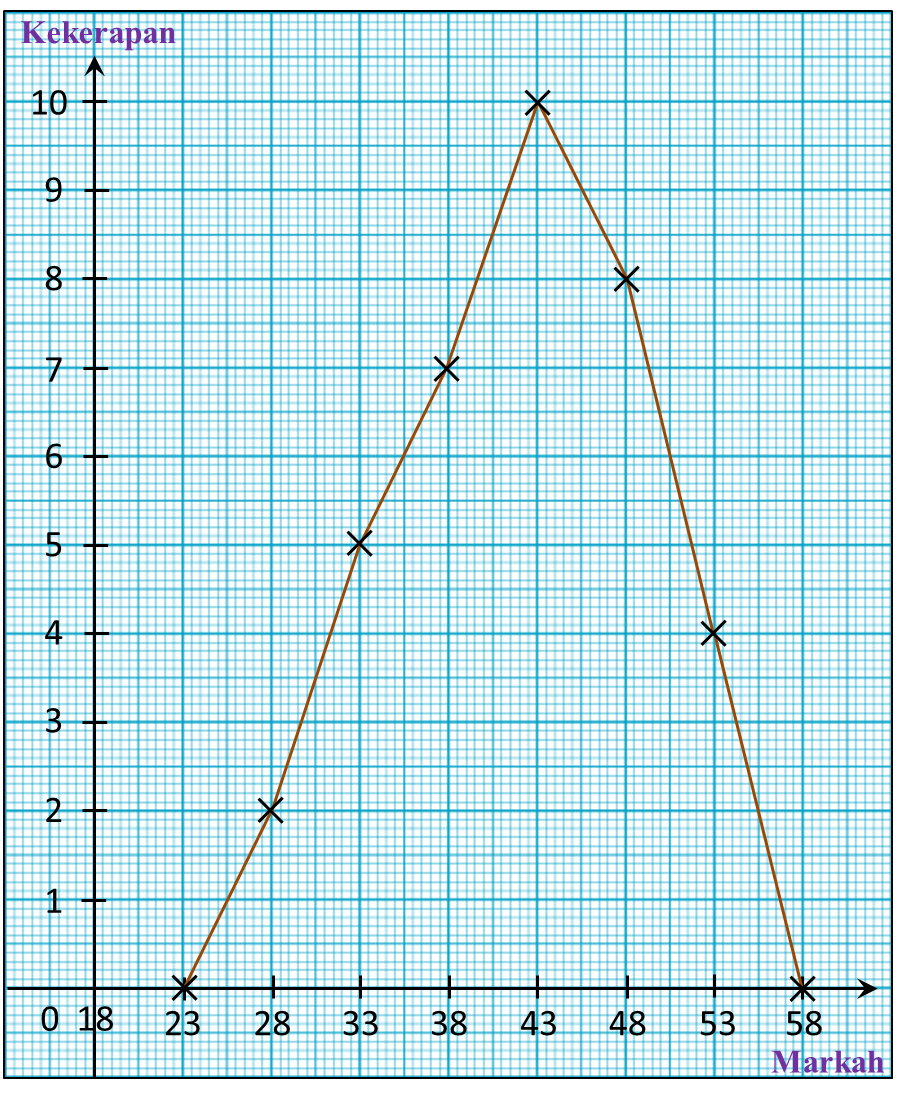
Rajah 10 menunjukkan suatu histogram yang mewakili jisim, dalam kg, bagi sekumpulan 100 orang murid.
 Rajah 10
Rajah 10
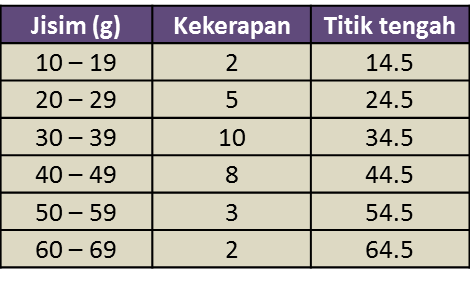
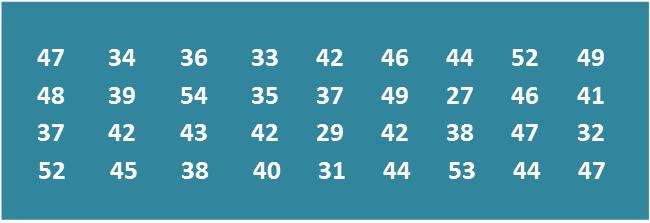
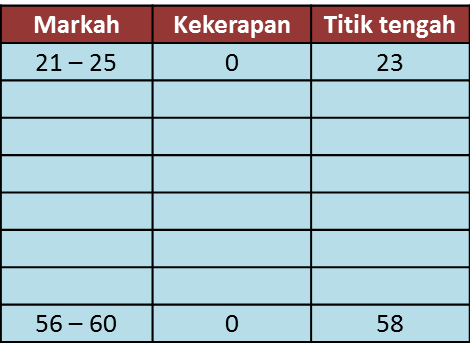
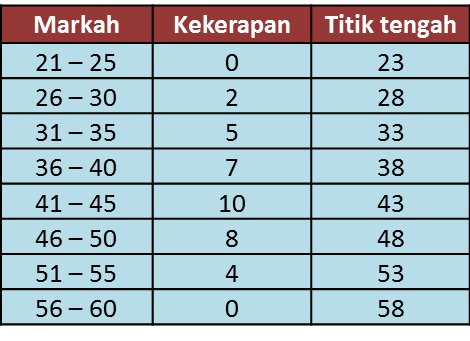
(a) Berdasarkan Rajah 10, lengkapkan Jadual 10 di ruang jawapan.
(b) Hitung min anggaran jisim bagi seorang murid.
(c) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.
Dengan menggunakan skala 2 cm kepada 10 kg pada paksi mengufuk dan 2 cm kepada 10 orang murid pada paksi mencancang, lukis satu ogif bagi data tersebut.
(d) Berdasarkan ogif yang dilukis di 10(c), nyatakan kuartil ketiga.
Jawapan:

Penyelesaian:
(a)

(b)

Min anggaran jisim=8110100=81.1 kg
(c)
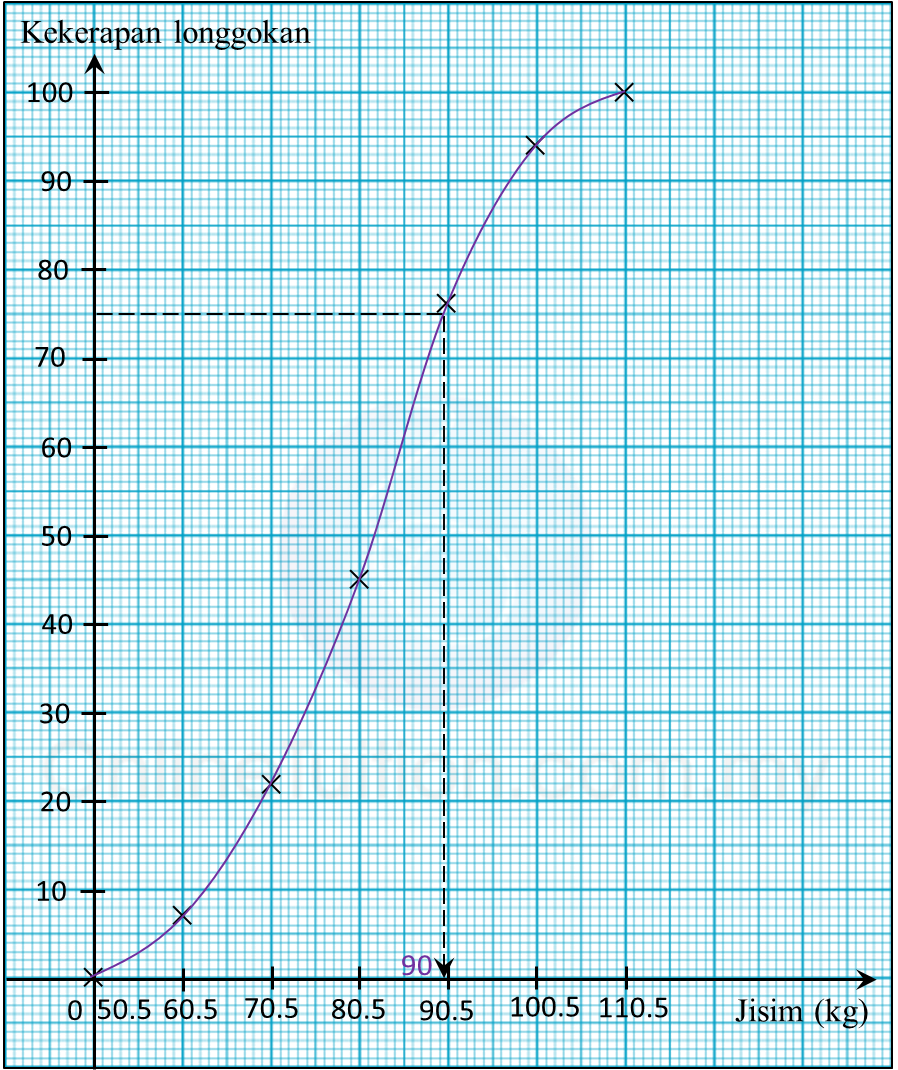
(d)
Kuartil ketiga
= murid ke-75
= 90.0 kg
Rajah 10 menunjukkan suatu histogram yang mewakili jisim, dalam kg, bagi sekumpulan 100 orang murid.
 Rajah 10
Rajah 10(a) Berdasarkan Rajah 10, lengkapkan Jadual 10 di ruang jawapan.
(b) Hitung min anggaran jisim bagi seorang murid.
(c) Untuk ceraian soalan ini, gunakan kertas graf. Anda boleh menggunakan pembaris fleksibel.
Dengan menggunakan skala 2 cm kepada 10 kg pada paksi mengufuk dan 2 cm kepada 10 orang murid pada paksi mencancang, lukis satu ogif bagi data tersebut.
(d) Berdasarkan ogif yang dilukis di 10(c), nyatakan kuartil ketiga.
Jawapan:

Penyelesaian:
(a)

(b)

Min anggaran jisim=8110100=81.1 kg
(c)

(d)
Kuartil ketiga
= murid ke-75
= 90.0 kg
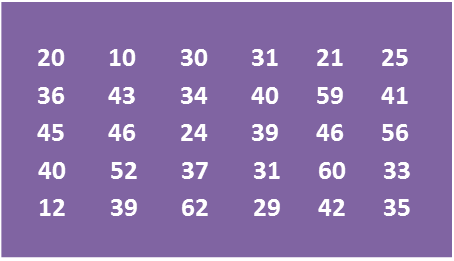 Rajah 9
Rajah 9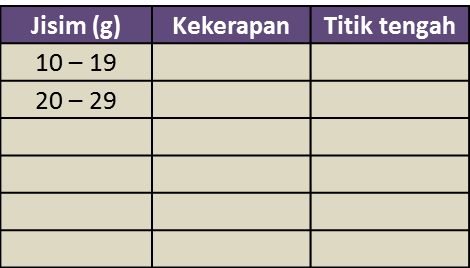
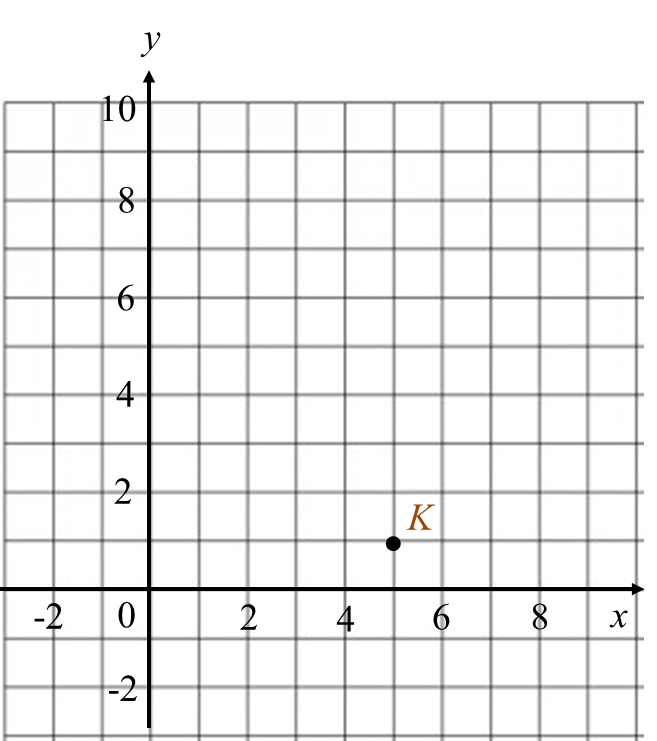 Rajah 8.1
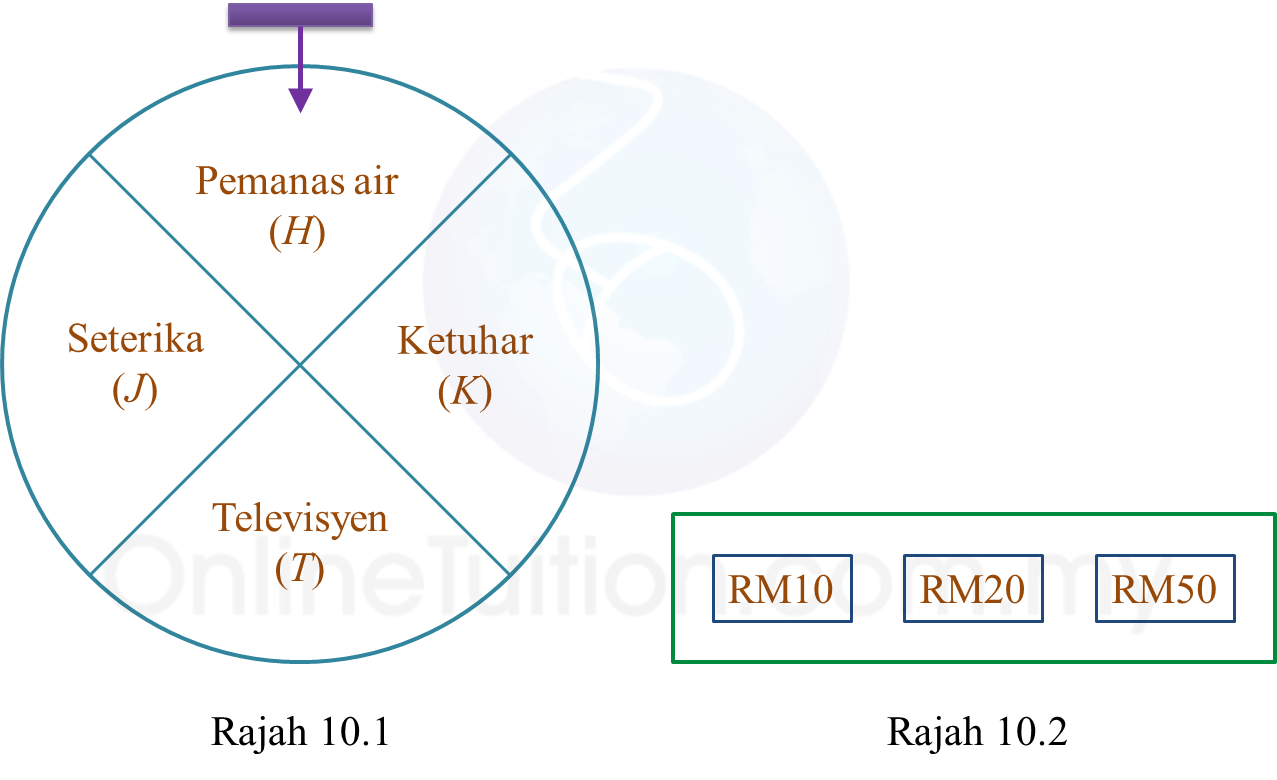
Rajah 8.1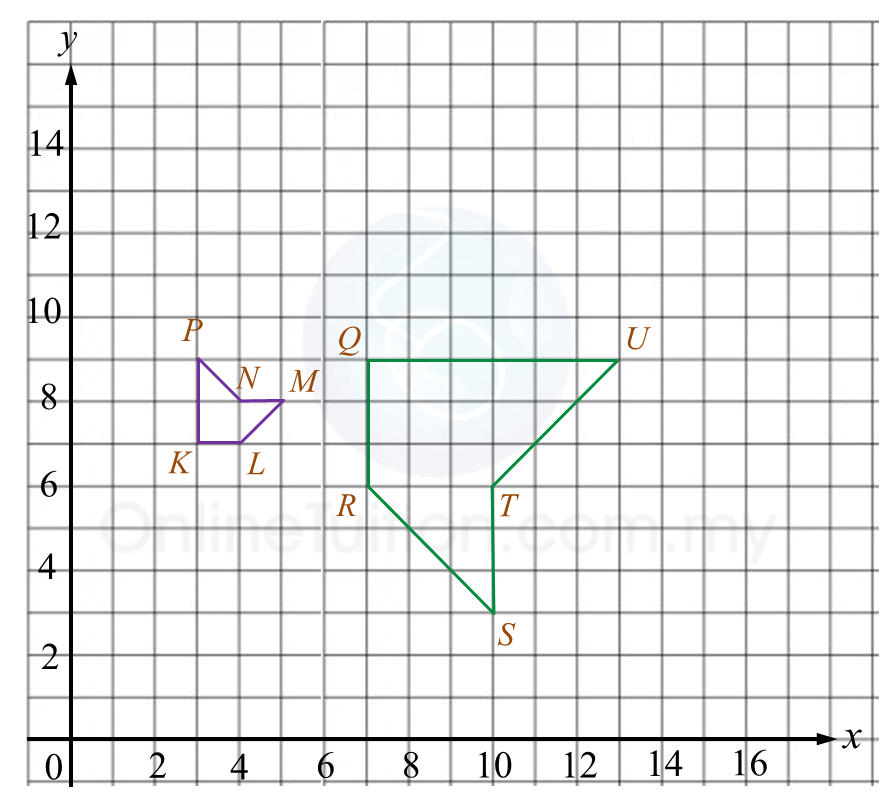 Rajah 10.2
Rajah 10.2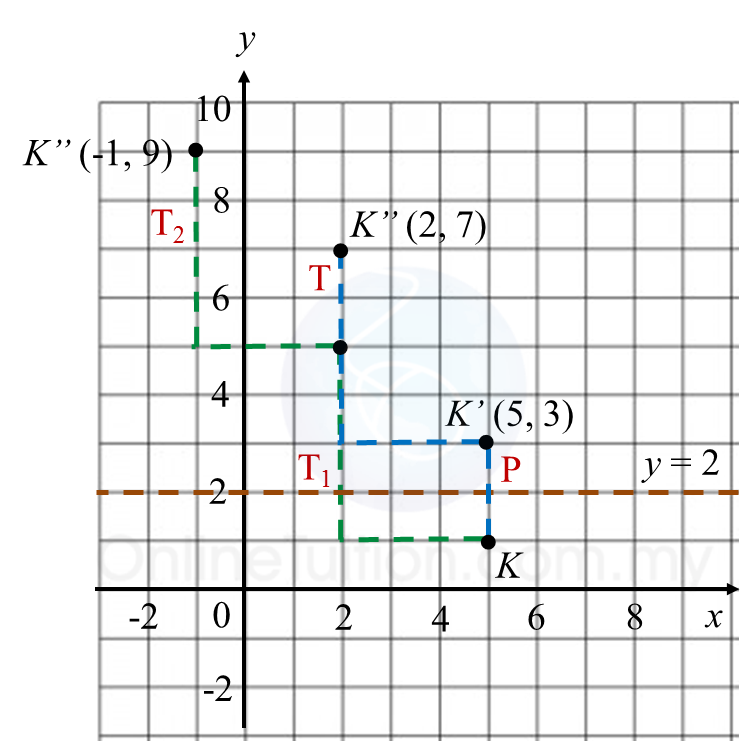
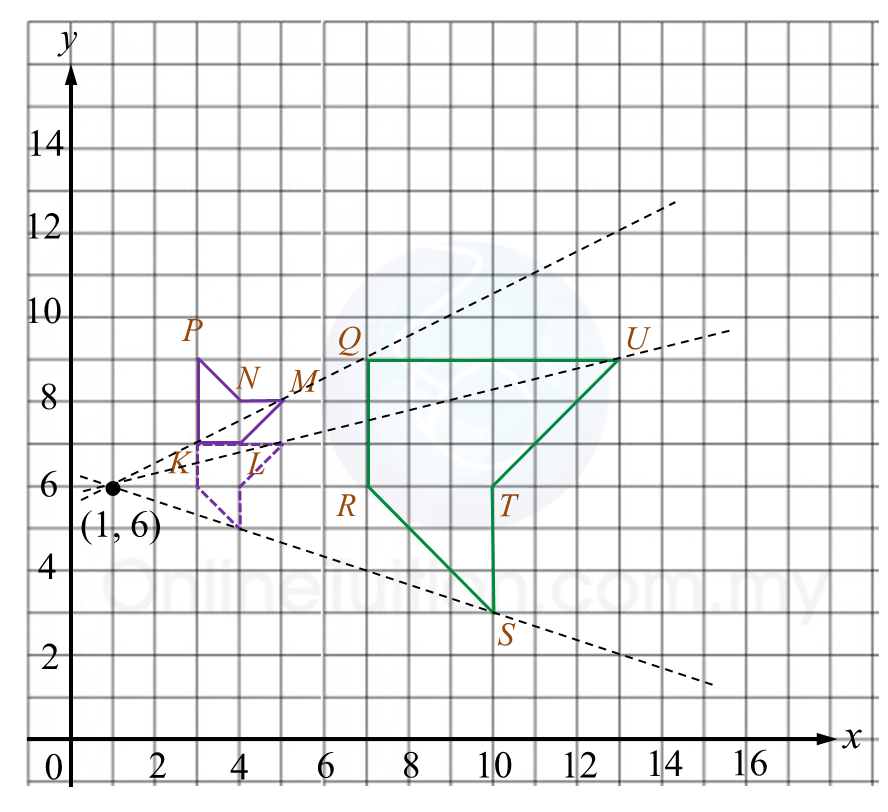
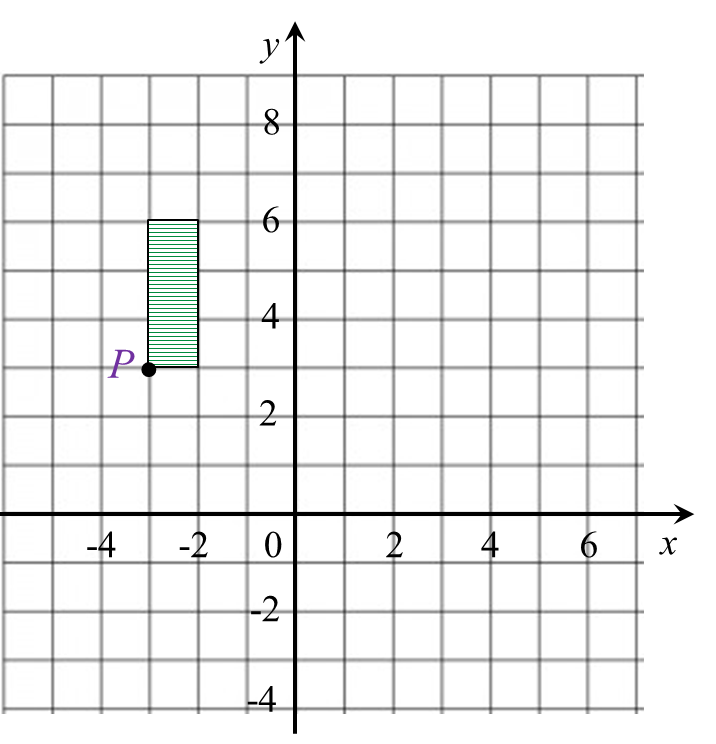 Rajah 7.1
Rajah 7.1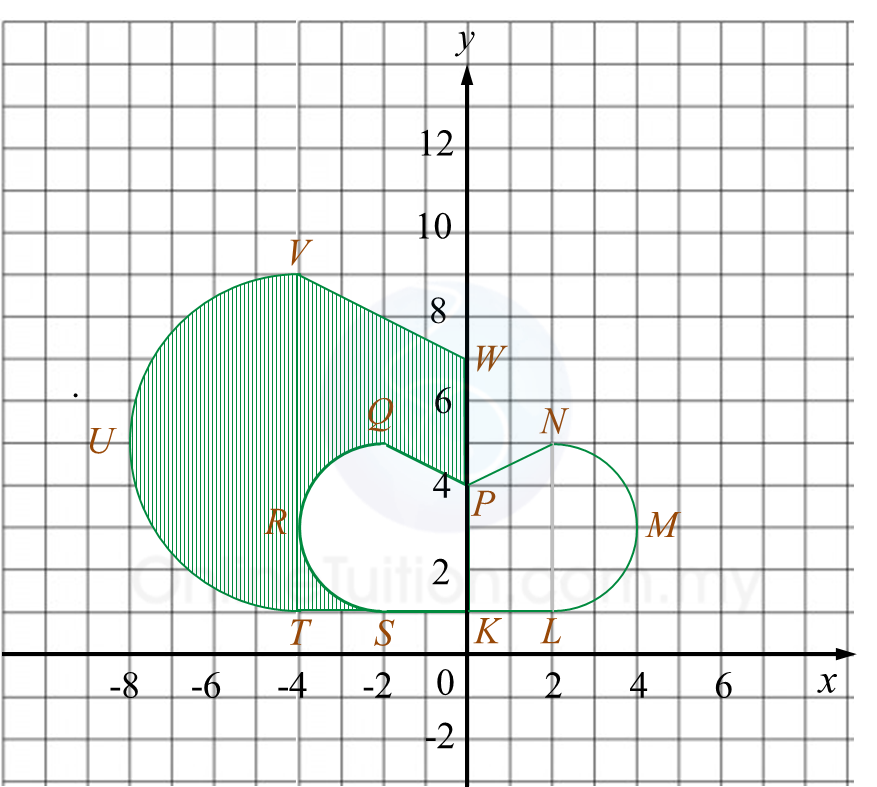 Rajah 7.2
Rajah 7.2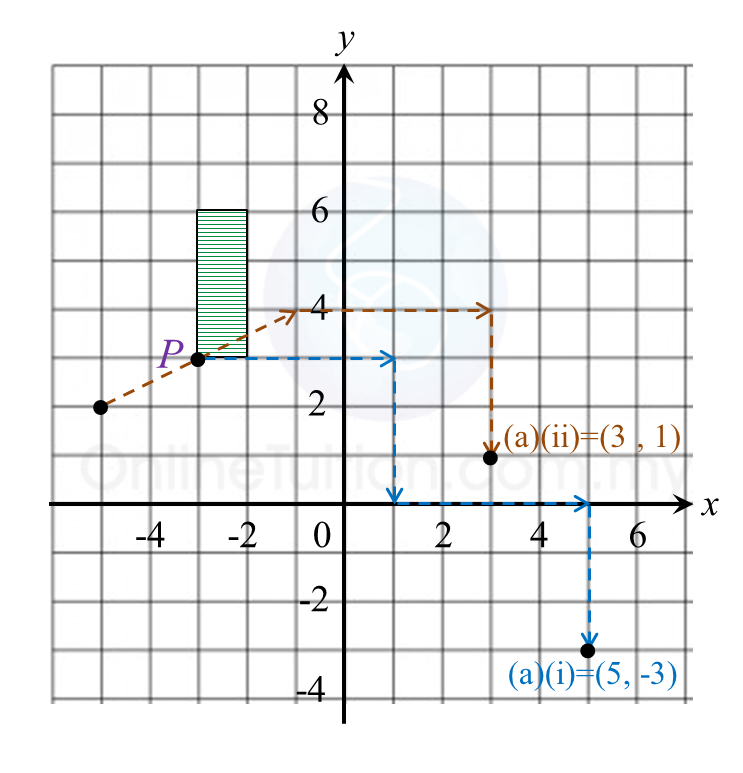





 Rajah
Rajah
 Rajah
Rajah