Soalan 6:
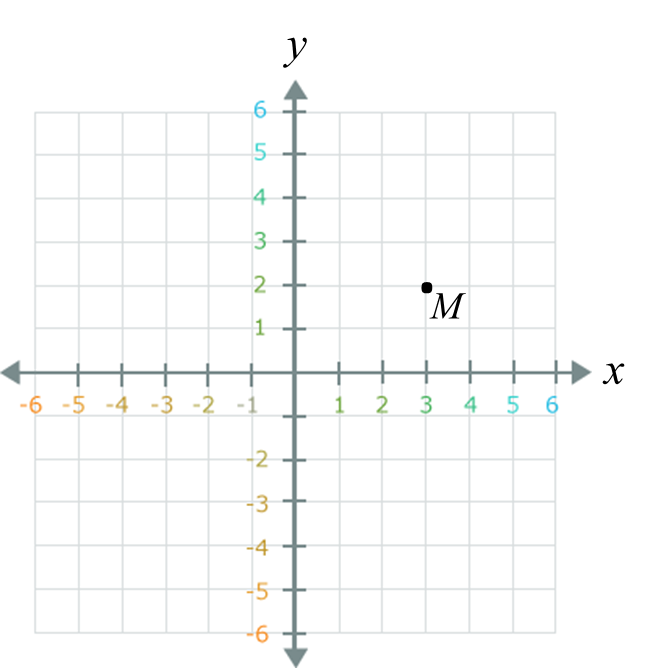
(a) Rajah 6.1 menunjukkan titik A dan titik B ditanda pada suatu satah Cartes.
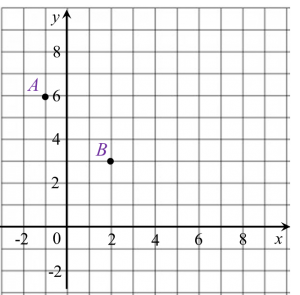 Rajah 6.1
Rajah 6.1
Penjelmaan R ialah satu putaran 90o, ikut arah jam pada pusat B.
Penjelmaan T ialah satu translasi
Nyatakan koordinat imej bagi titik A di bawah setiap penjelmaan berikut:
(i) RT,
(ii) R2.
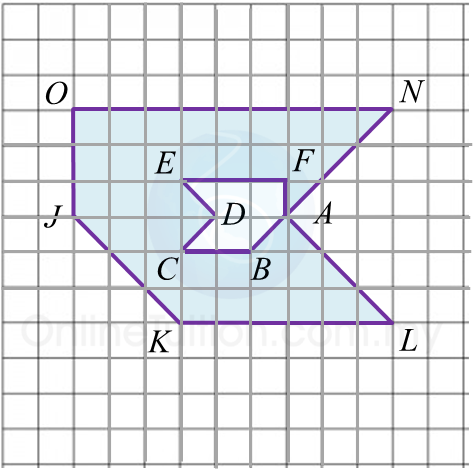
(b) Rajah 8.2 menunjukkan tiga trapezium ABCD, PQRS dan TUVS, dilukis pada suatu satah Cartes.
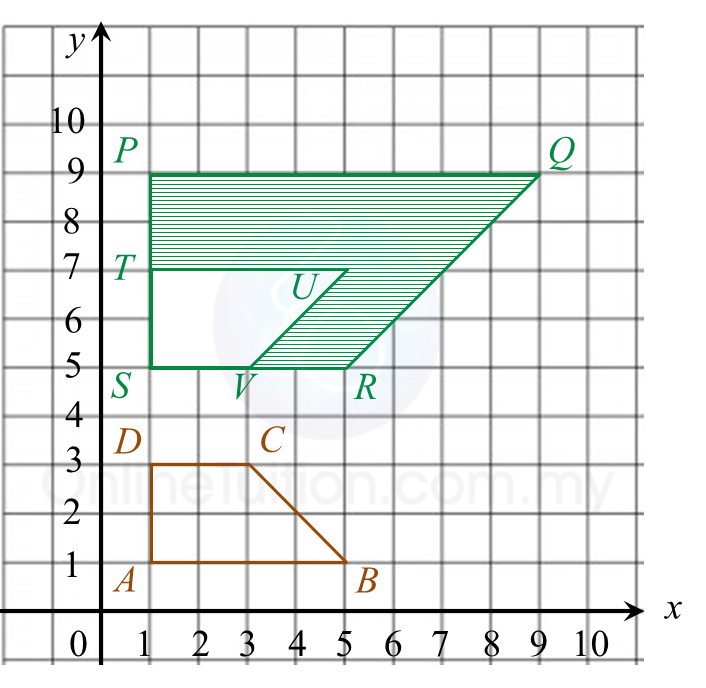 Rajah 6.2
Rajah 6.2
(i) Trapezium PQRS ialah imej bagi trapezium ABCD di bawah gabungan penjelmaan MN.
Huraikan selengkapnya penjelmaan:
(a) N,
(b) M.
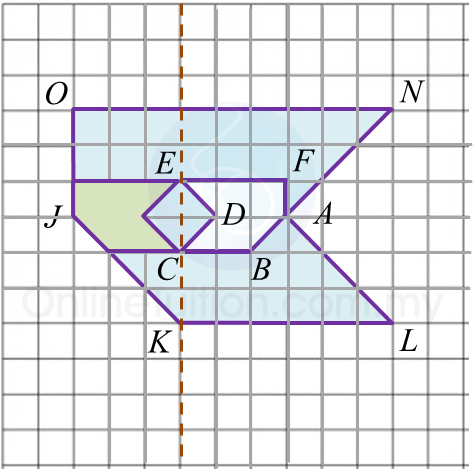
(ii) Diberi bahawa trapezium ABCD mewakili suatu kawasan yang mempunyai luas 30 m2.
Hitungkan luas, dalam m2, kawasan yang diwakili oleh rantau berlorek.
Penyelesaian:
(a)
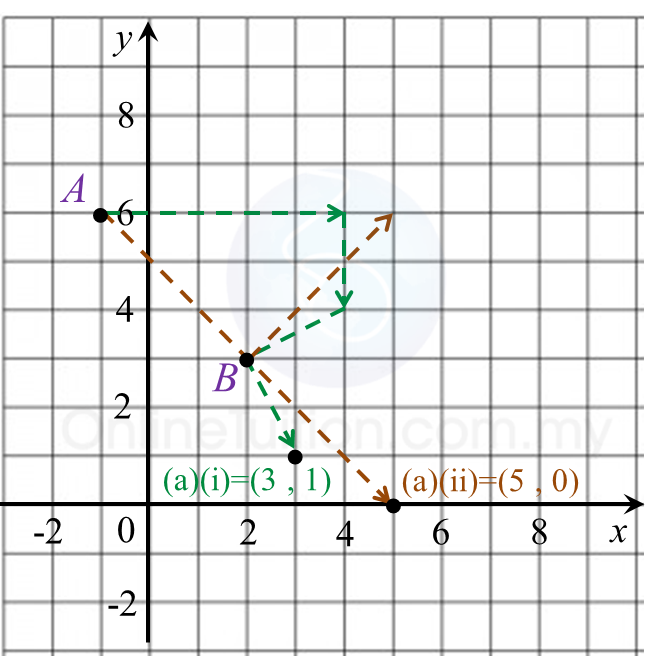
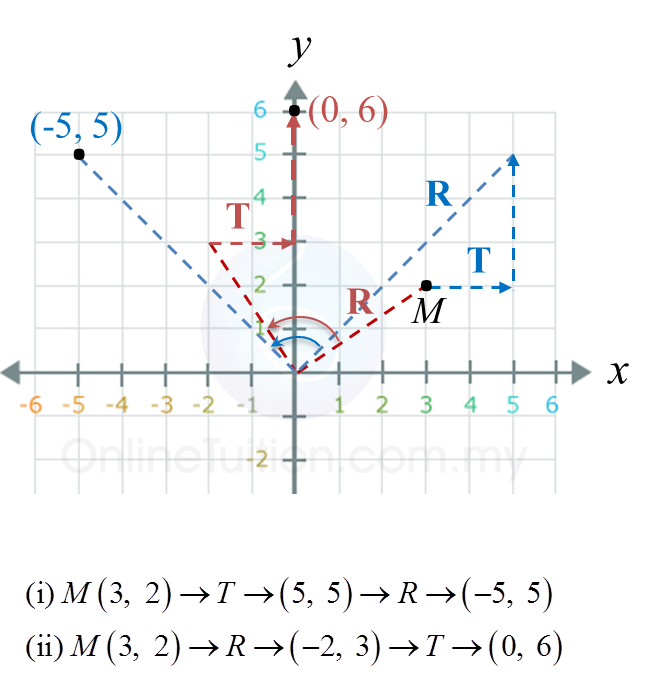
(i) A (–1, 6) → T → (4, 4 ) → R → (3, 1)
(ii) A (–1, 6) → R → (5, 6) → R → (5, 0)
(b)(i)(a)
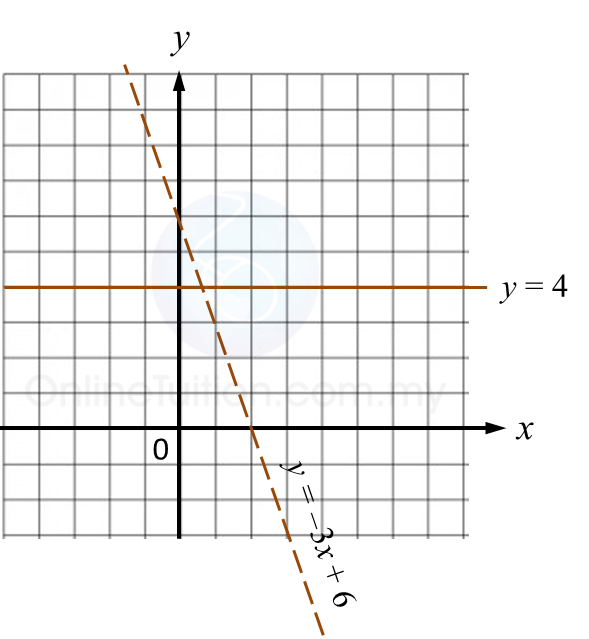
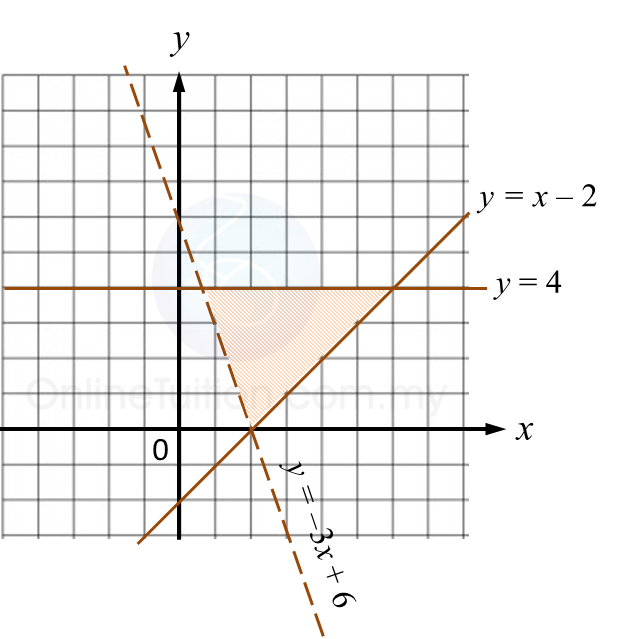
N: Satu pantulan pada garis lurus y = 4.
(b)(ii)(b)
M: Satu pembesaran pada pusat S (1, 5) dengan faktor skala 2.
(b)(ii)
Luas PQRS = (faktor skala)2 x Luas objek ABCD
= 22 x 30
= 120 m2
Oleh itu,
Luas rantau berlorek
= Luas PQRS – luas ABCD
= 120 – 30
= 90 m2
(a) Rajah 6.1 menunjukkan titik A dan titik B ditanda pada suatu satah Cartes.
 Rajah 6.1
Rajah 6.1Penjelmaan R ialah satu putaran 90o, ikut arah jam pada pusat B.
Penjelmaan T ialah satu translasi
Nyatakan koordinat imej bagi titik A di bawah setiap penjelmaan berikut:
(i) RT,
(ii) R2.
(b) Rajah 8.2 menunjukkan tiga trapezium ABCD, PQRS dan TUVS, dilukis pada suatu satah Cartes.
 Rajah 6.2
Rajah 6.2(i) Trapezium PQRS ialah imej bagi trapezium ABCD di bawah gabungan penjelmaan MN.
Huraikan selengkapnya penjelmaan:
(a) N,
(b) M.
(ii) Diberi bahawa trapezium ABCD mewakili suatu kawasan yang mempunyai luas 30 m2.
Hitungkan luas, dalam m2, kawasan yang diwakili oleh rantau berlorek.
Penyelesaian:
(a)

(i) A (–1, 6) → T → (4, 4 ) → R → (3, 1)
(ii) A (–1, 6) → R → (5, 6) → R → (5, 0)
(b)(i)(a)
N: Satu pantulan pada garis lurus y = 4.
(b)(ii)(b)
M: Satu pembesaran pada pusat S (1, 5) dengan faktor skala 2.
(b)(ii)
Luas PQRS = (faktor skala)2 x Luas objek ABCD
= 22 x 30
= 120 m2
Oleh itu,
Luas rantau berlorek
= Luas PQRS – luas ABCD
= 120 – 30
= 90 m2