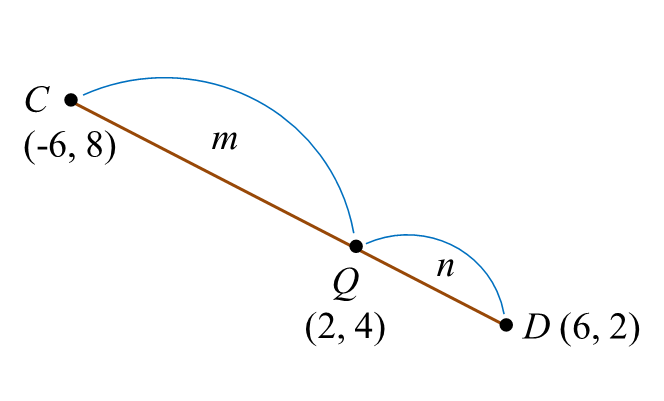
Soalan 8 (10 markah):
(a) Jisim bagi buah tembikai susu yang dihasilkan di sebuah ladang bertaburan secara normal dengan min 0.8 kg dan sisihan piawai 0.25 kg. Buah tempikai susu itu dikelaskan kepada tiga gred A, B dan C mengikut jisimnya:
Gred A > Gred B > Gred C
(i) Jisim minimum bagi sebiji tembikai susu gred A ialah 1.2 kg.
Jika sebiji tembikai susu diambil secara rawak dari ladang itu, cari kebarangkalian bahawa buah tembikai susu itu adalah gred A.
(ii) Cari jisim minimum, dalam kg, buah tembikai susu gred B jika 20% daripada buah-buah tembikai susu itu adalah gred C.
(b) Dalam permainan Menembak Itik di taman hiburan, kebarangkalian untuk menang ialah 25%.
Jacky telah membeli tiket untuk bermain permainan itu sebanyak n kali. Kebarangkalian untuk Jacky menang sekali dalam permainan itu adalah 10 kali ganda kebarangkalian kalah dalam semua permainan.
(i) Cari nilai n.
(ii) Hitung sisihan piawai bagi bilangan kemenangan.
Penyelesaian:
μ = 0.8 kg, σ = 0.25 kg
(a)(i)
P(gred A)=P(X>1.2) =P(Z>1.2−0.80.25) =P(Z>1.6) =0.0548
(a)(ii)
P(gred C)=0.2P(X<m)=0.2P(Z<m−0.80.25)=0.2P(Z<−0.842)=0.2 m−0.80.25=−0.842 m−0.8=−0.2105 m=0.5895Jisim minimum buah tembikai susugred B adalah sama dengan jisim maximum buah tembikai susu gred C.Jisim minimum gred B=0.5895 kg
(b)
p=0.25, X=B(n, 0.25)P(X=r)=Cnrprqn−r =Cnr(0.25)r(0.75)n−r
(b)(i)
P(X=1)=10 P(X=0)Cnr(0.25)1(0.75)n−r=10×Cn0(0.25)0(0.75)nCn1(0.25)1(0.75)n−1=10×1×1×(0.75)nn×0.25×(0.75)n−1=10×(0.75)n0.25n×(0.75)n−10.75n=100.25n×0.75−1=1014n(34)−1=1014n(43)=1013n=10n=30
(b)(ii)
n=30, p=0.25, q=0.75Sisihan piawai=√npq=√30×0.25×0.75=2.372
(a) Jisim bagi buah tembikai susu yang dihasilkan di sebuah ladang bertaburan secara normal dengan min 0.8 kg dan sisihan piawai 0.25 kg. Buah tempikai susu itu dikelaskan kepada tiga gred A, B dan C mengikut jisimnya:
Gred A > Gred B > Gred C
(i) Jisim minimum bagi sebiji tembikai susu gred A ialah 1.2 kg.
Jika sebiji tembikai susu diambil secara rawak dari ladang itu, cari kebarangkalian bahawa buah tembikai susu itu adalah gred A.
(ii) Cari jisim minimum, dalam kg, buah tembikai susu gred B jika 20% daripada buah-buah tembikai susu itu adalah gred C.
(b) Dalam permainan Menembak Itik di taman hiburan, kebarangkalian untuk menang ialah 25%.
Jacky telah membeli tiket untuk bermain permainan itu sebanyak n kali. Kebarangkalian untuk Jacky menang sekali dalam permainan itu adalah 10 kali ganda kebarangkalian kalah dalam semua permainan.
(i) Cari nilai n.
(ii) Hitung sisihan piawai bagi bilangan kemenangan.
Penyelesaian:
μ = 0.8 kg, σ = 0.25 kg
(a)(i)
P(gred A)=P(X>1.2) =P(Z>1.2−0.80.25) =P(Z>1.6) =0.0548
(a)(ii)
P(gred C)=0.2P(X<m)=0.2P(Z<m−0.80.25)=0.2P(Z<−0.842)=0.2 m−0.80.25=−0.842 m−0.8=−0.2105 m=0.5895Jisim minimum buah tembikai susugred B adalah sama dengan jisim maximum buah tembikai susu gred C.Jisim minimum gred B=0.5895 kg
(b)
p=0.25, X=B(n, 0.25)P(X=r)=Cnrprqn−r =Cnr(0.25)r(0.75)n−r
(b)(i)
P(X=1)=10 P(X=0)Cnr(0.25)1(0.75)n−r=10×Cn0(0.25)0(0.75)nCn1(0.25)1(0.75)n−1=10×1×1×(0.75)nn×0.25×(0.75)n−1=10×(0.75)n0.25n×(0.75)n−10.75n=100.25n×0.75−1=1014n(34)−1=1014n(43)=1013n=10n=30
(b)(ii)
n=30, p=0.25, q=0.75Sisihan piawai=√npq=√30×0.25×0.75=2.372
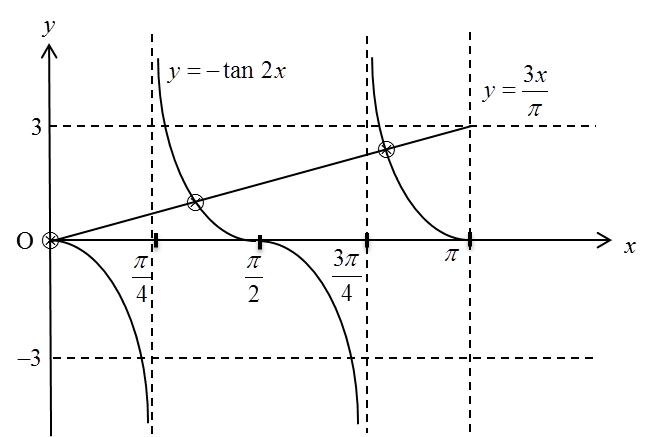
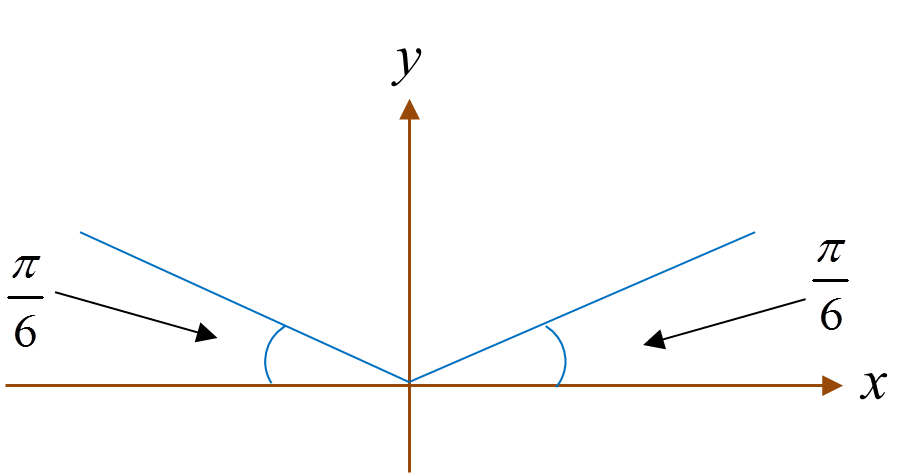
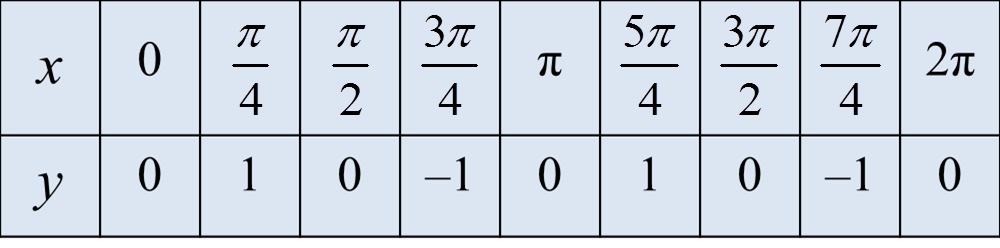
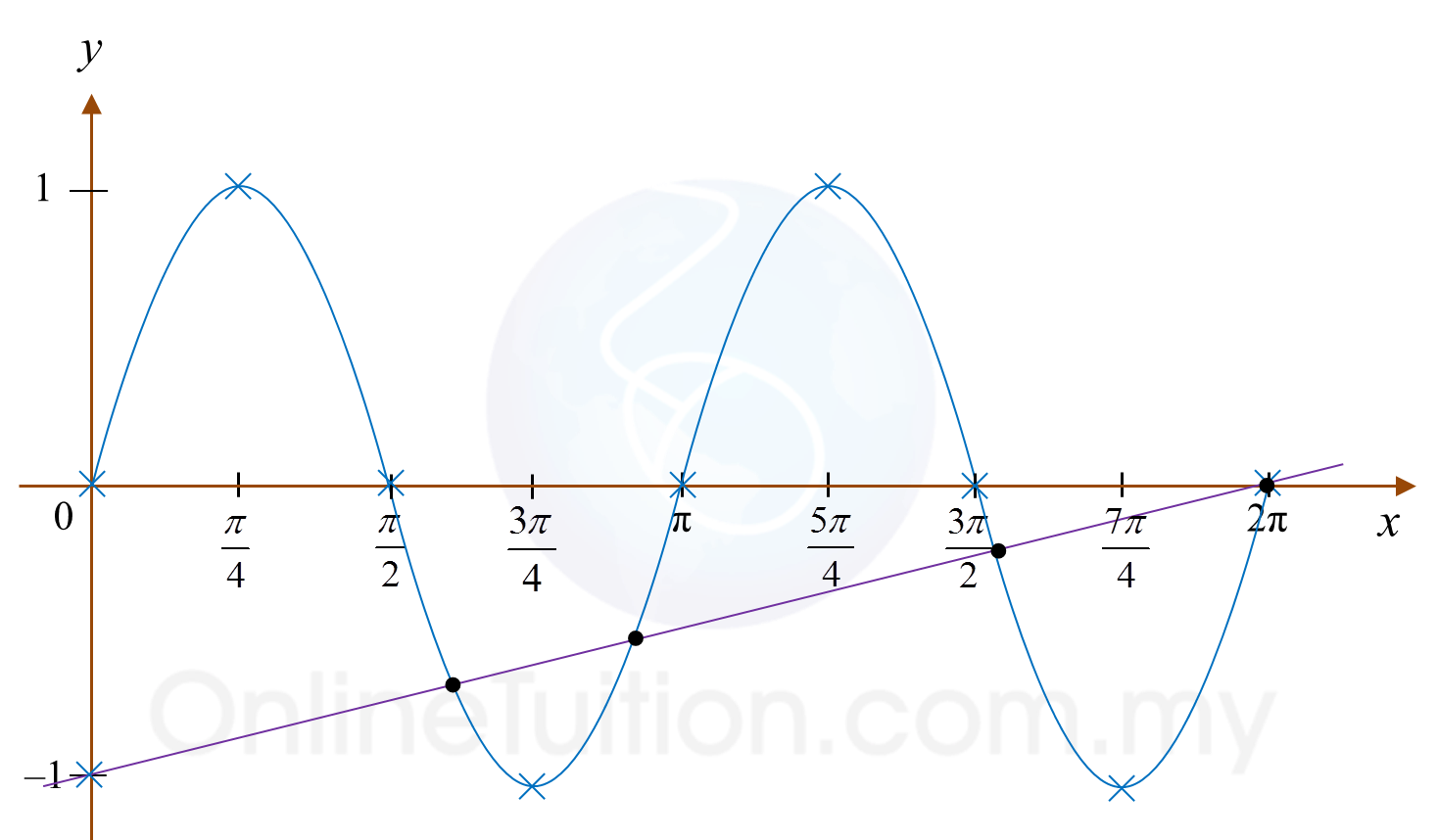
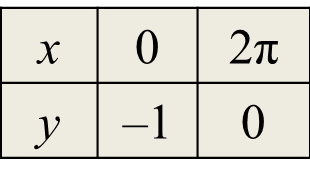
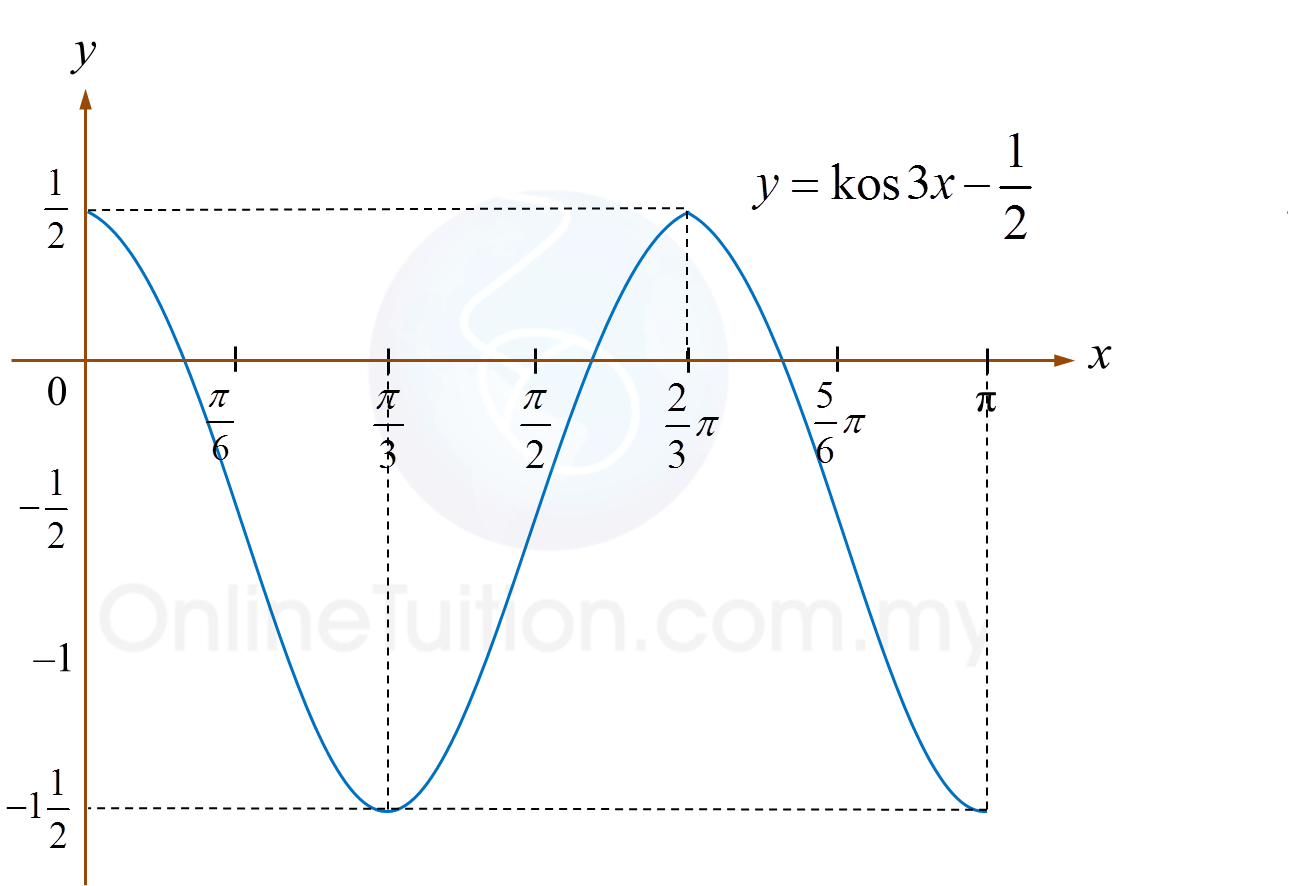


 Rajah 1
Rajah 1