Soalan 3:
Sebuah kotak mengandungi 48 guli yang terdiri daripada guli merah dan guli hijau. Sebiji guli dipilih secara rawak dari kotak itu. Kebarangkalian sebiji guli merah dipilih ialah
Berapakah bilangan guli merah yang perlu ditambah ke dalam kotak itu supaya kebarangkalian sebiji guli merah dipilih ialah
Penyelesaian:
Sebuah kotak mengandungi 48 guli yang terdiri daripada guli merah dan guli hijau. Sebiji guli dipilih secara rawak dari kotak itu. Kebarangkalian sebiji guli merah dipilih ialah
Berapakah bilangan guli merah yang perlu ditambah ke dalam kotak itu supaya kebarangkalian sebiji guli merah dipilih ialah
Penyelesaian:
Soalan 4:
Sebuah kotak mengandungi 5 keping kad merah, 3 keping kad kuning dan beberapa keping kad hijau. Sekeping kad dipilih secara rawak daripada kotak itu. Diberi kebarangkalian memilih kad kuning ialah , cari kebarangkalian memilih sekeping kad yang bukan warna hijau.
Penyelesaian:
Sebuah kotak mengandungi 5 keping kad merah, 3 keping kad kuning dan beberapa keping kad hijau. Sekeping kad dipilih secara rawak daripada kotak itu. Diberi kebarangkalian memilih kad kuning ialah , cari kebarangkalian memilih sekeping kad yang bukan warna hijau.
Penyelesaian:
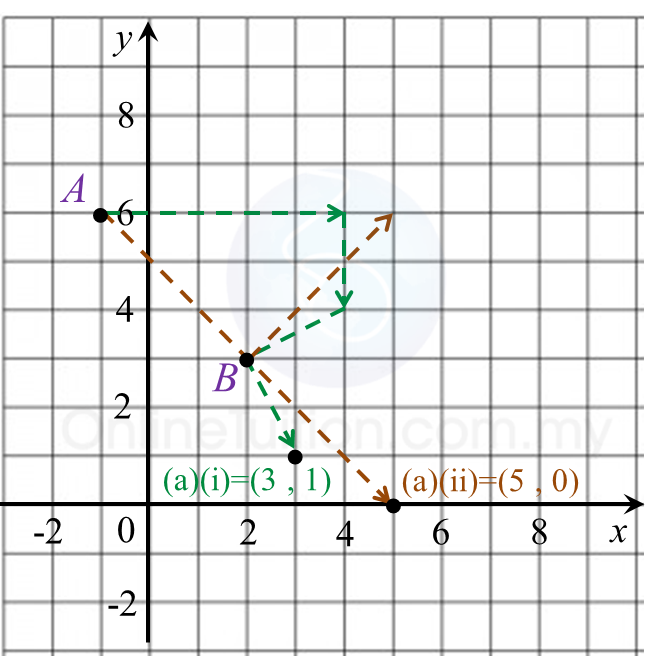
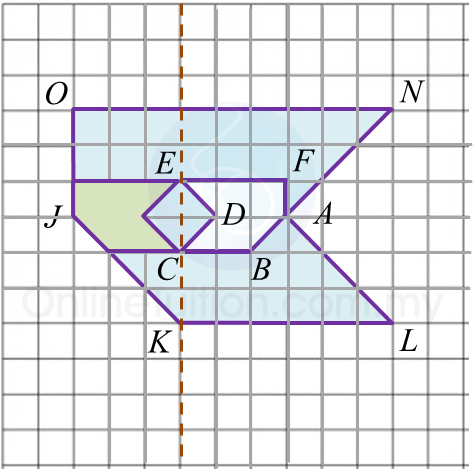
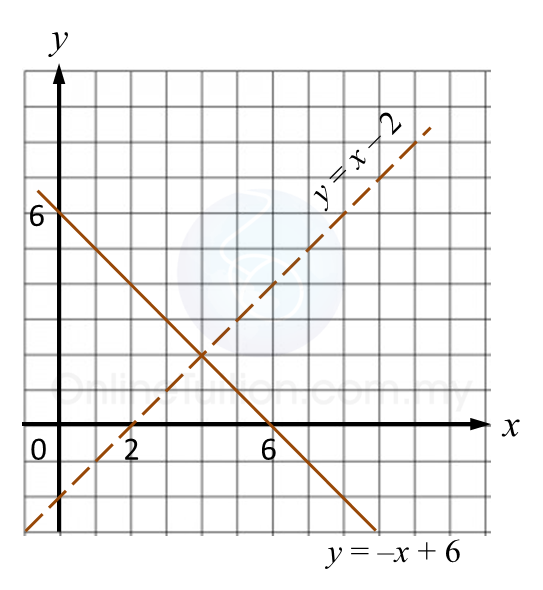
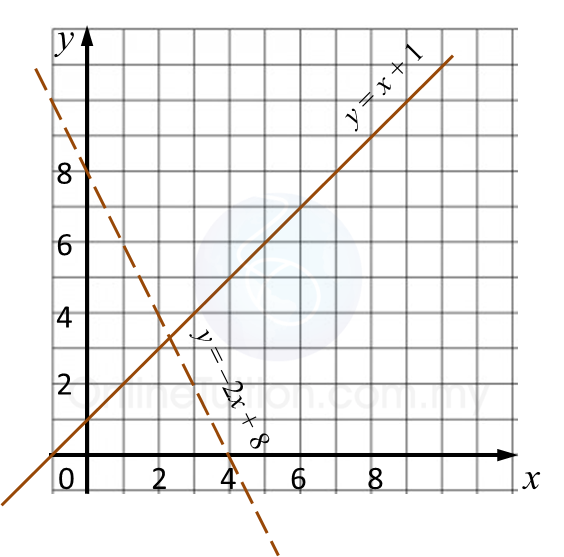
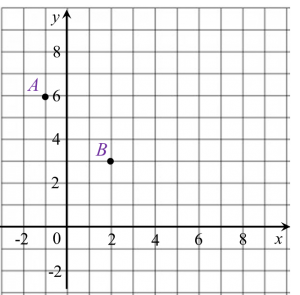 Rajah 6.1
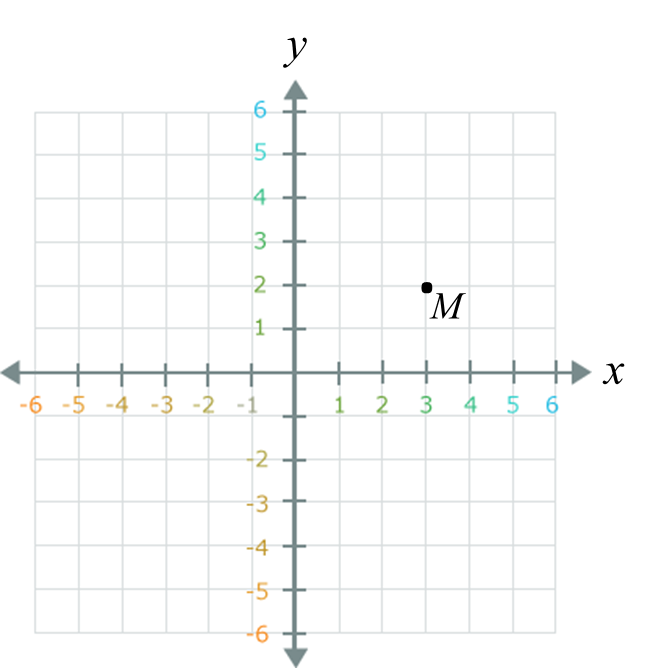
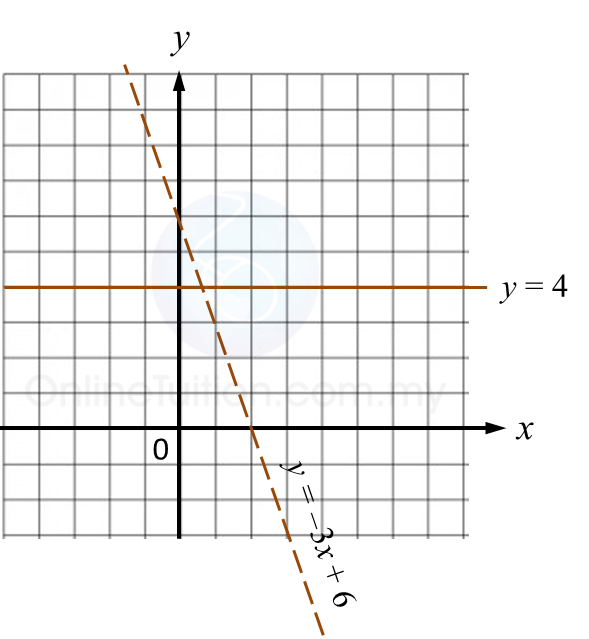
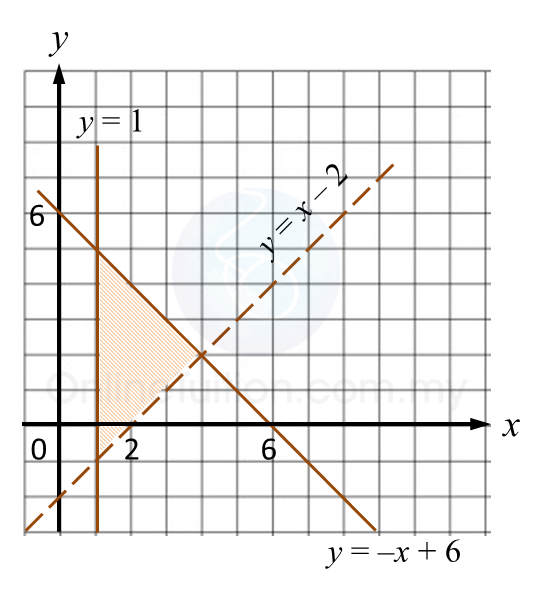
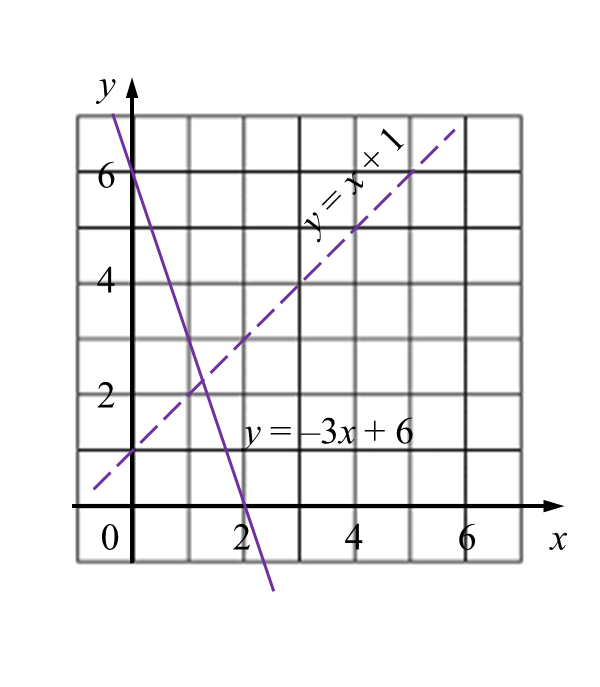
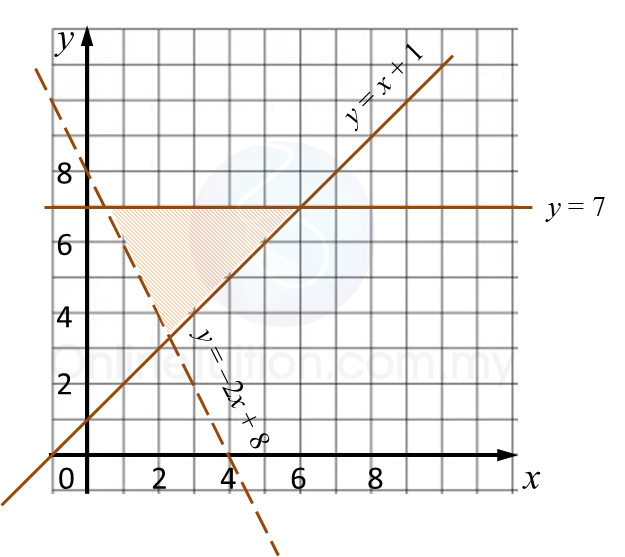
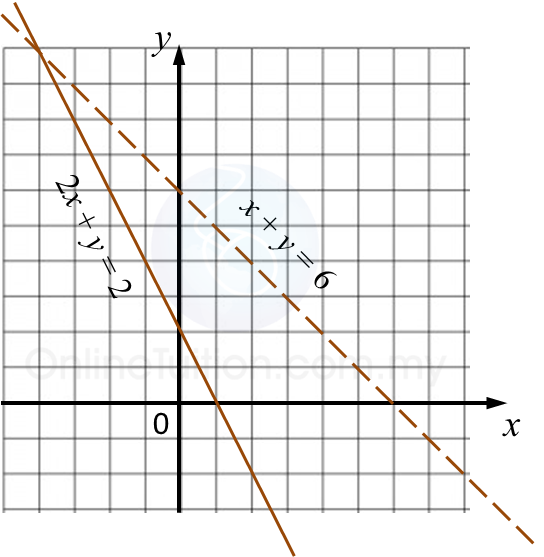
Rajah 6.1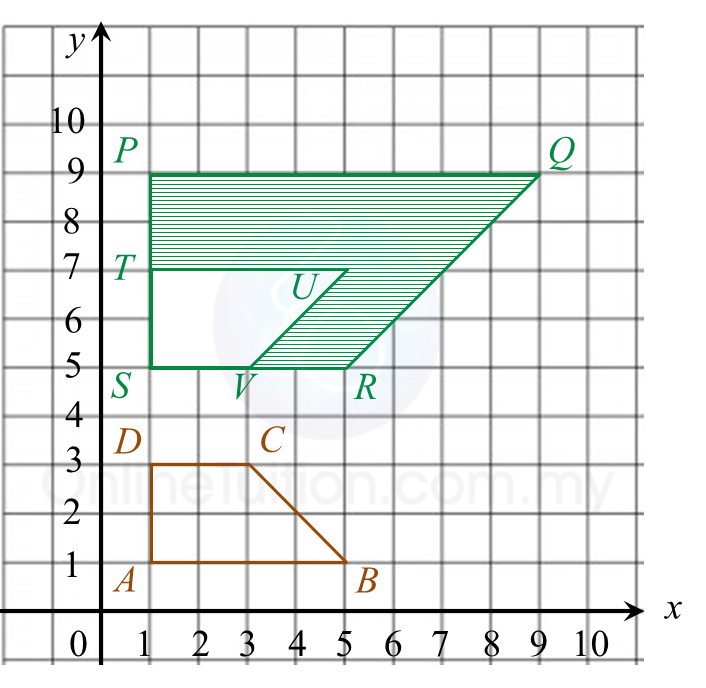 Rajah 6.2
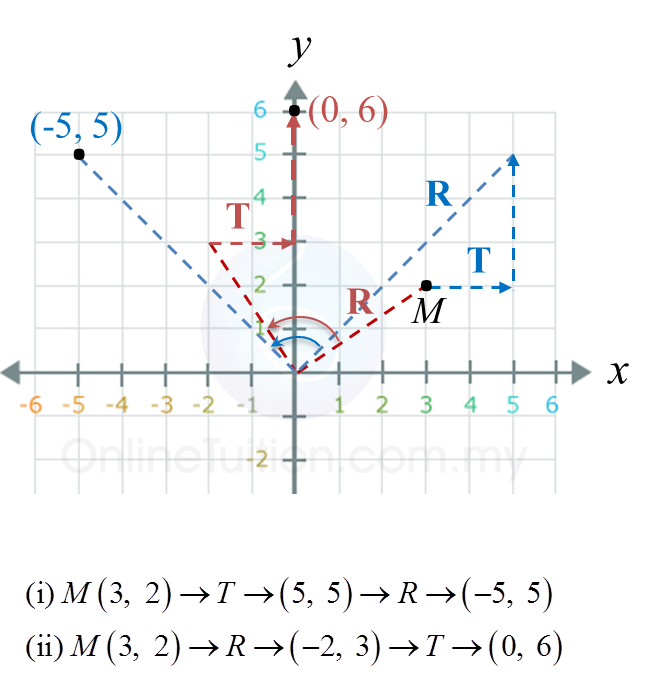
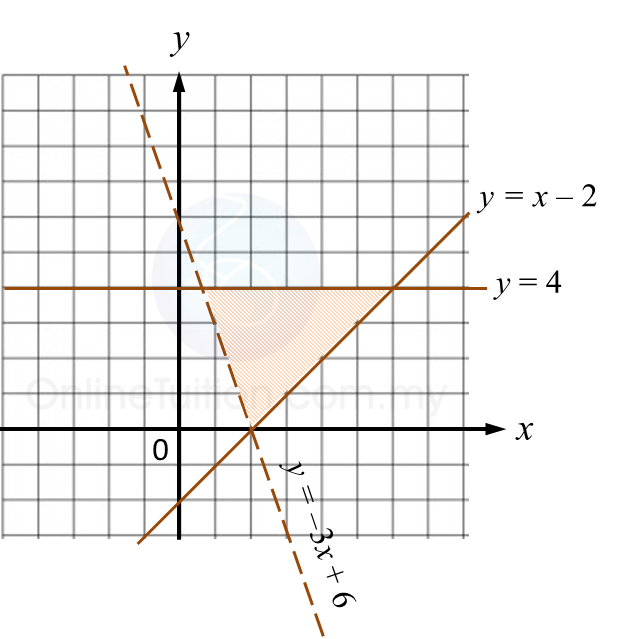
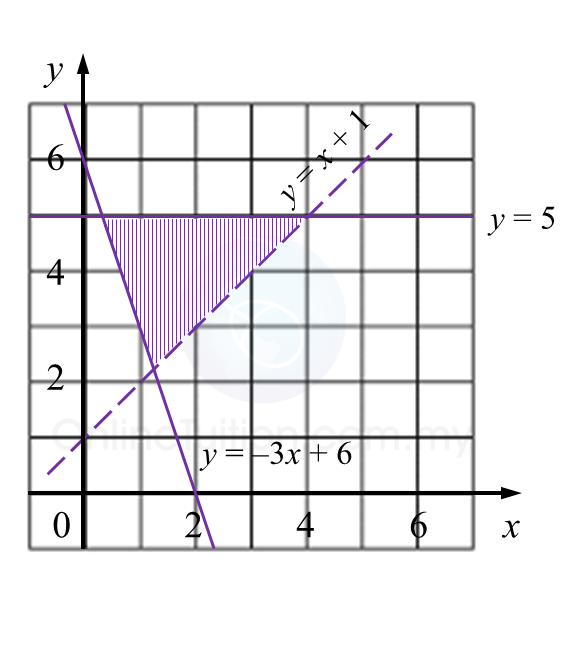
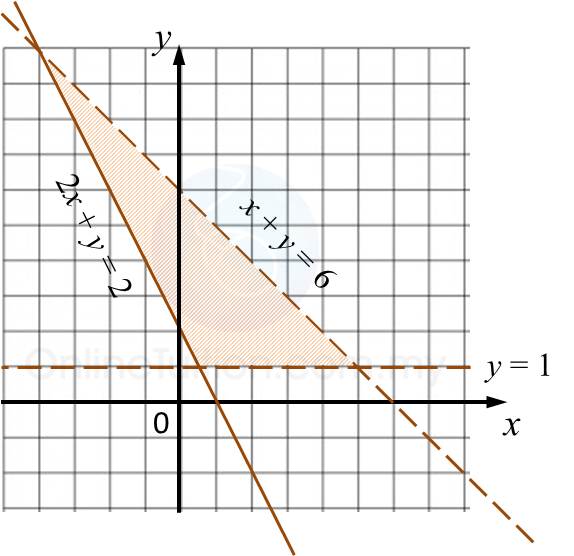
Rajah 6.2