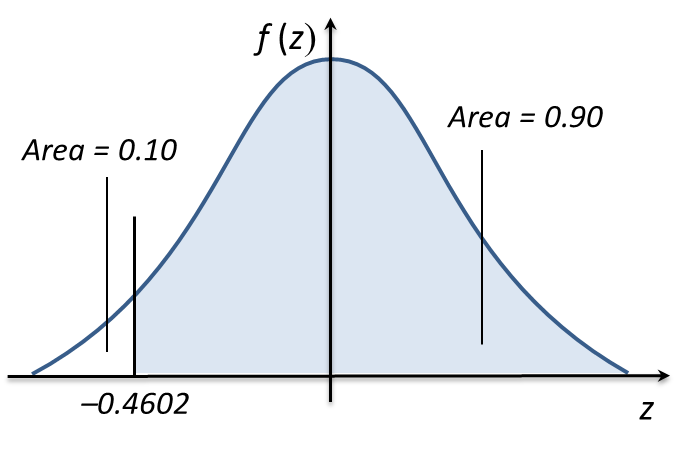
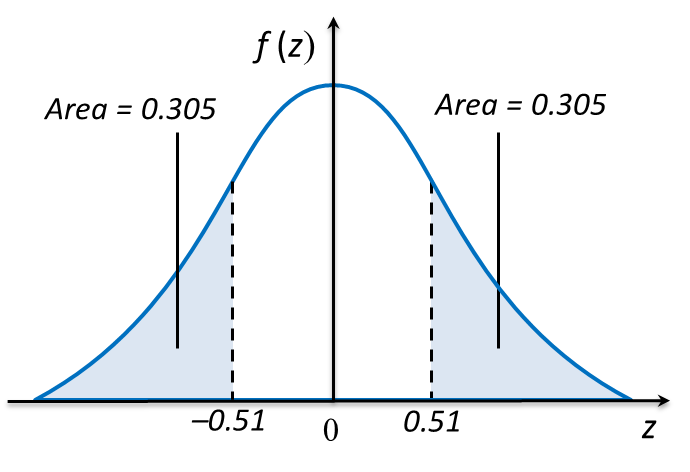
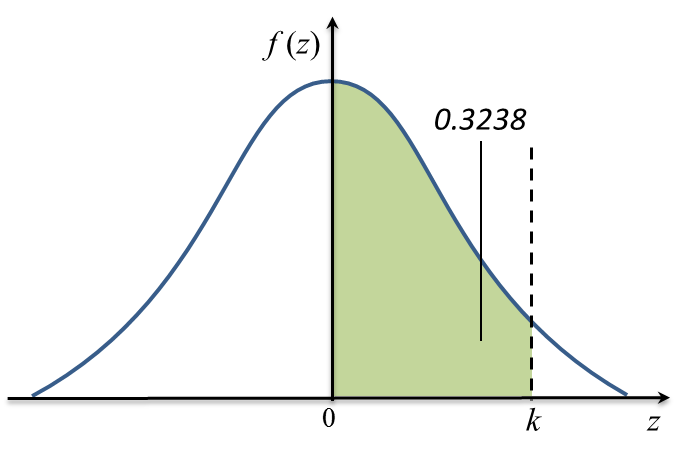
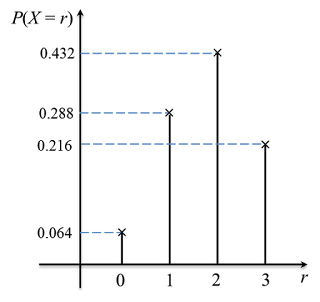Question 1:
Solution:
(a)
X− Number of students who failed Chemistry.X~B(n,p)X~B(6, 25)P(X=r)=cnr.pr.qn−rP(X≤2)=P(X=0)+P(X=1)+P(X=2)=C60(25)0(35)6+C61(25)1(35)5+C62(25)2(35)4=0.0467+0.1866+0.3110=0.5443
(b)
X~B(n,p)X~B(200, 25)Mean of X=np=200×25=80Standard deviation of X=√npq=√200×25×35=√48=6.93
In a school examination, 2 students out of 5 students failed Chemistry.
(a) If 6 students are chosen at random, find the probability that not more than 2 students failed Chemistry.
(b) If there are 200 Form 4 students in that school, find the mean and standard deviation of the number of students who failed Chemistry.
(a)
X− Number of students who failed Chemistry.X~B(n,p)X~B(6, 25)P(X=r)=cnr.pr.qn−rP(X≤2)=P(X=0)+P(X=1)+P(X=2)=C60(25)0(35)6+C61(25)1(35)5+C62(25)2(35)4=0.0467+0.1866+0.3110=0.5443
(b)
X~B(n,p)X~B(200, 25)Mean of X=np=200×25=80Standard deviation of X=√npq=√200×25×35=√48=6.93
Question 2:
Solution:
(a)
(b)
Therefore, the minimum number of mangoes that have to be chosen so that the probability of obtaining at least one rotten mango is greater than 0.85 is 37.
5% of the supply of mangoes received by a supermarket are rotten.
(a) If a sample of 12 mangoes is chosen at random, find the probability that at least two mangoes are rotten.
(b) Find the minimum number of mangoes that have to be chosen so that the probability of obtaining at least one rotten mango is greater than 0.85.
(a)
X ~ B (12, 0.05)
1 – P (X ≤ 1)
= 1 – [P (X = 0) + P (X = 1)]
= 1 – [
C120
(0.05)0 (0.95)12 +
C121
(0.05)1 (0.95)11]
= 1 – 0.8816
= 0.1184
(b)
P (X ≥ 1) > 0.85
1 – P (X = 0) > 0.85
P (X = 0) < 0.15
Cn0
(0.05)0(0.95)n < 0.15
n lg 0.95 < lg 0.15
n > 36.98
n = 37
Therefore, the minimum number of mangoes that have to be chosen so that the probability of obtaining at least one rotten mango is greater than 0.85 is 37.