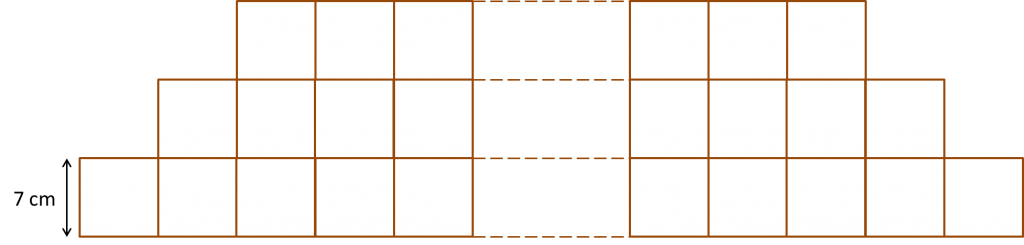
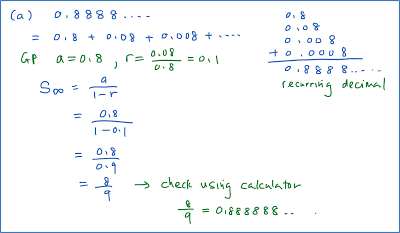
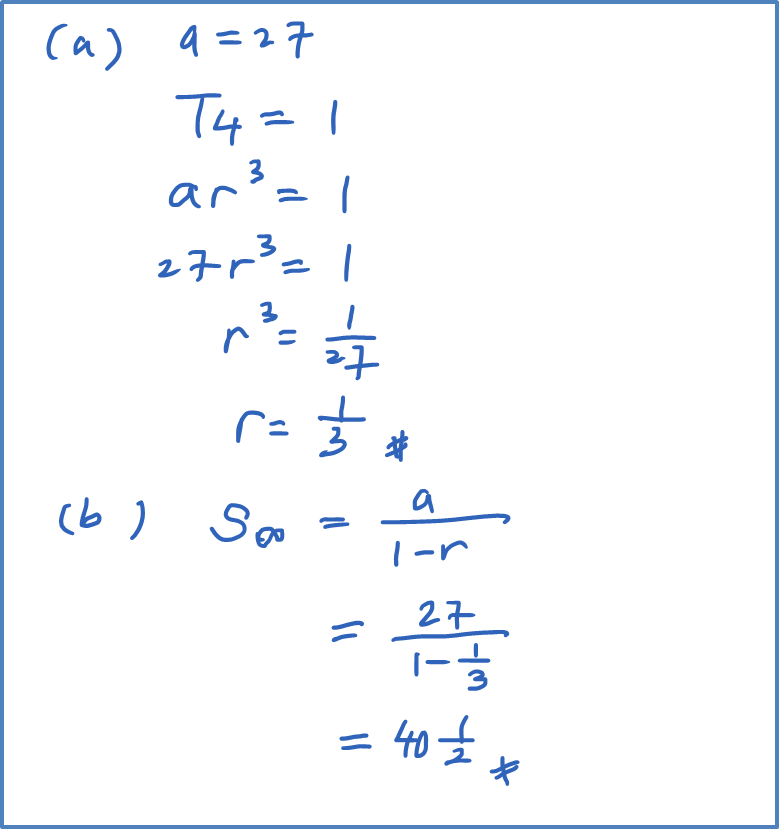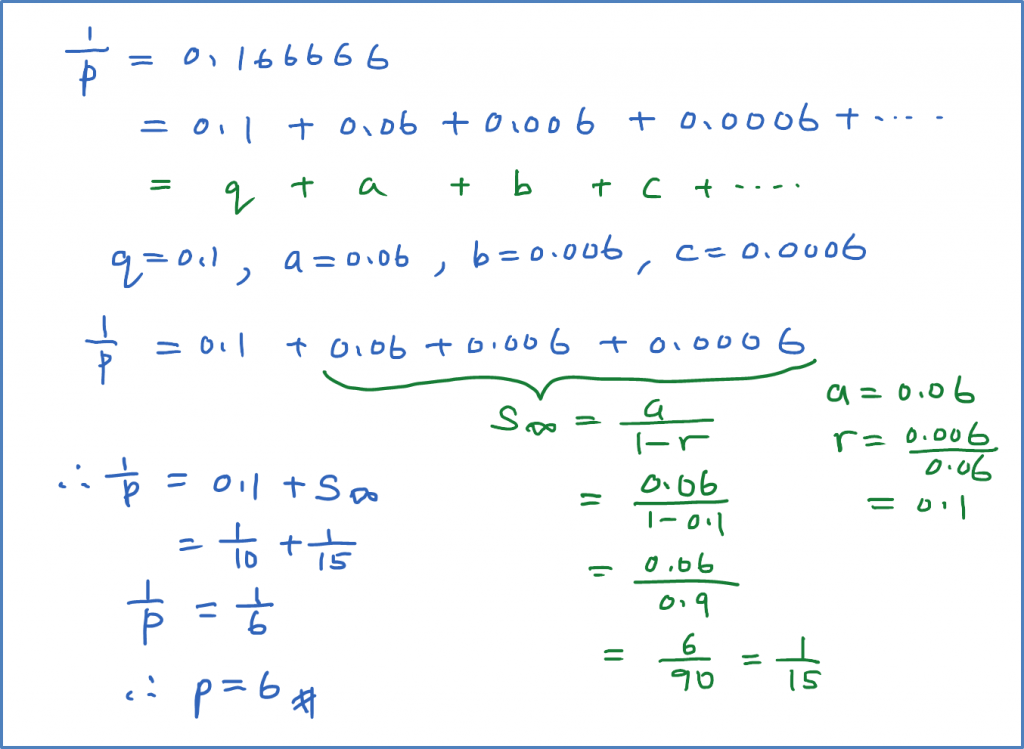The nth Term of Arithmetic Progression (Examples)
Example 1:
If the 20th term of an arithmetic progression is 14 and the 40th term is –6,
Find
Find
(a) the first term and the common difference,
(b) the 10th term.
Solution:
(a)
T20 = 14
a + 19d = 14 ----- (1) ← (Tn = a + (n– 1) d
T40 = – 6
a + 39d = – 6 ----- (2)
(2) – (1),
20d = – 20
d = – 1
Substitute d = – 1 into (1),
a + 19 (– 1) = 14
a = 33
(b)
T10 = a + 9d
T10 = 33 + 9 (– 1)
T10 = 24
Example 2:
The 3rd term and the 7th term of an arithmetic progression are 20 and 12 respectively.
(a) Calculate the 20th term.
(b) Find the term whose value is – 34.
Solution:
(a)
T3 = 20
a + 2d = 20 ----- (1) ← (Tn= a + (n – 1) d
T7 = 12
a + 6d = 12 ----- (2)
(2) – (1),
4d = – 8
d = – 2
Substitute d = – 2 into (1),
a + 2 (– 2) = 20
a = 24
T20 = a + 19d
T20 = 24 + 19 (– 2)
T20 = –4
(b)
Tn = –34
a + (n – 1) d = –34
24 + (n – 1) (–2) = –34
(n – 1) (–2) = –58
n – 1 = 29
n = 30