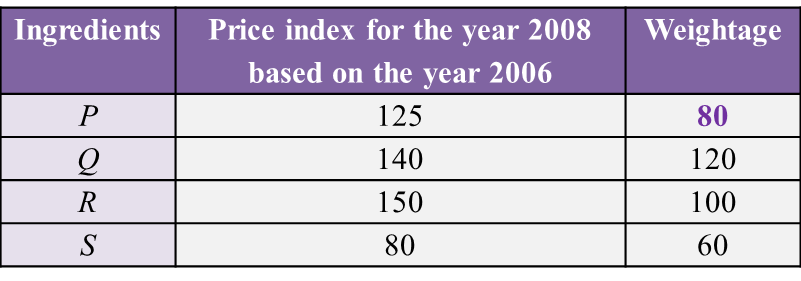
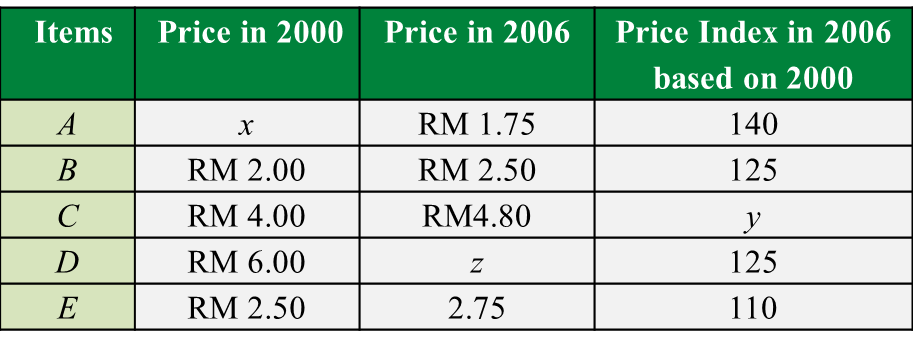
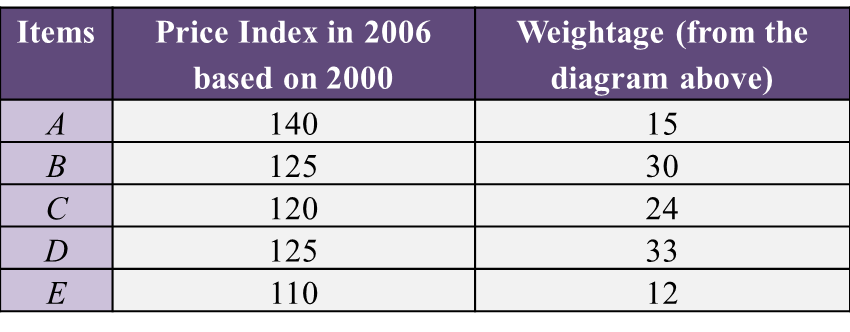
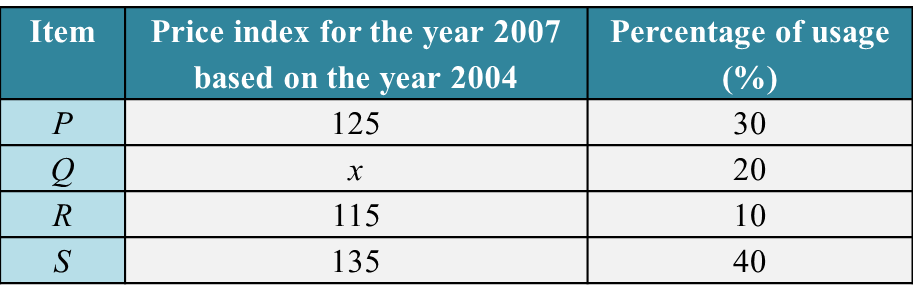
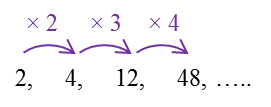2. Geometric Progression
(A) Characteristics of Geometric Progressions
Geometric progression is a progression in which the ratio of any term to the immediate term before is a constant. The constant is called common ratio, r.
Example:
Determine whether or not each of the following number sequences is a geometric progression (GP).
(a) 1, 4, 16, 64, …..
(b) 10, –5, 2.5, –1.25, …..
(c) 2, 4, 12, 48, …..
(d) –6, 1, 8, 15, …..
Solution:
[Smart Tips: For GP, times a fixed number every time to get the next time.]
(a)
This is a GP, a =1, r = 4.
(b)
This is a GP, a =1, r = – ½.
(c)
This is NOT a GP.
This is because the ratio of each term to its preceding term is not a similar constant.
(B) The steps to prove whether a given number sequence is a geometric progression.
Step 1: List down any three consecutive terms. [Example: T1, T2, T3.]
Step 2: Calculate the values of
Step 3: If
, then the number sequence is a geometric
progression.
progression.
Step 4: If
, then the number sequence is not a geometric progression.