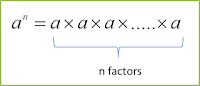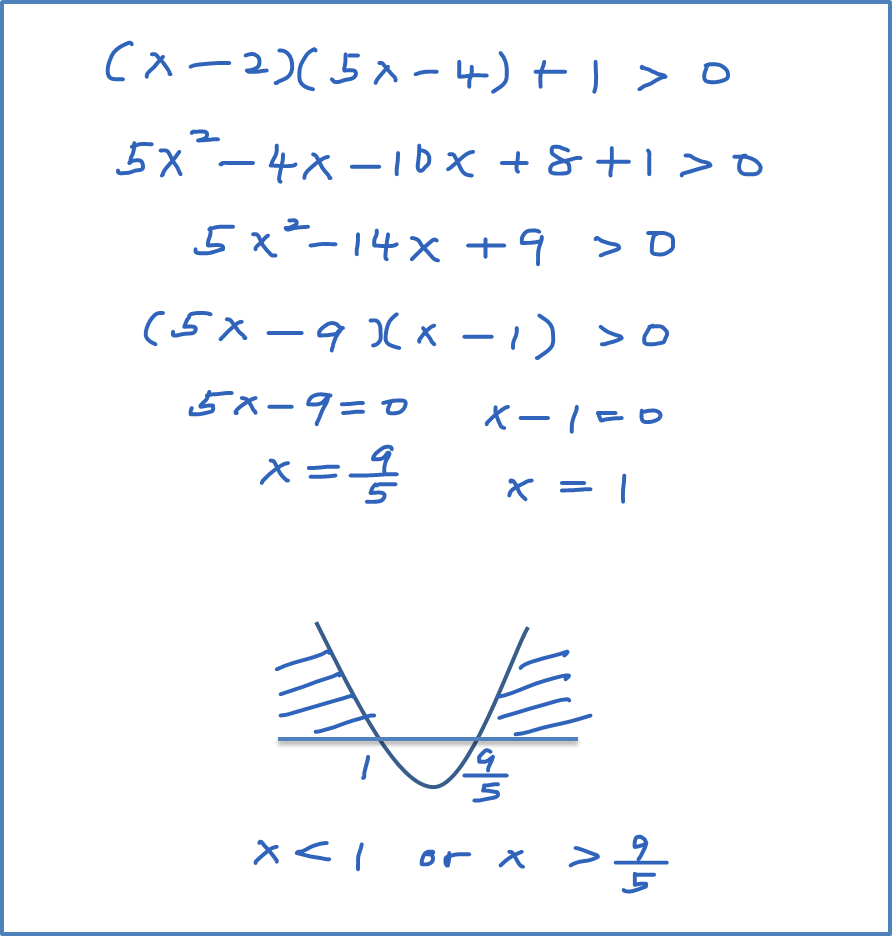Yearly Archives: 2020
5.2a Laws of Logarithms
5.2a Laws of Logarithms
5.2 Logarithms
5.1 Indices and Laws of Indices (Part 2)
5.1 Indices and Laws of Indices (Part 2)
(C) Fractional Indices
Example 1:
Find the value of the followings:Solution:
Example 2:
Find the value of the followings:
Solution:
(D) Laws of Indices
Indices and Laws of Indices (Part 1)
Positive Integral Indices
When a real number a is multiplied by itself n times, the result is the nth power of a.
Example: 5×5×5×5 = 54 (5 to the power of 4)
In general, if a is any real number and n is a positive integer, then
The integer n is called the index or exponent and a is the base.
5.1 Indices and Laws of Indices (Part 1)
(A) Zero IndicesThe zero index of any number is equal to one.
a 0 = 1, where a ≠ 0 |
Example 1:
Find the value of the followings:
(a) 2500
(b) 0.5130
Solution:
(a) 2500 = 1
(b) 0.5130 = 1
(B) Negative Integral Indices
Example 2:
Find the value of the followings:
(a) 102 -1
(b) –6 -3
Solution:
Quadratic Functions, SPM Practice (Long Questions)
Question 3:
Given that the quadratic function f(x) = 2x2 – px + p has a minimum value of –18 at x = 1.
(a) Find the values of p and q.
(b) With the value of p and q found in (a), find the values of x, where graph f(x) cuts the x-axis.
(c) Hence, sketch the graph of f(x).
Solution:
(a)
(b)
(c)
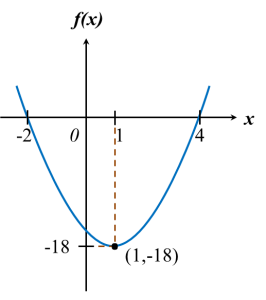
Given that the quadratic function f(x) = 2x2 – px + p has a minimum value of –18 at x = 1.
(a) Find the values of p and q.
(b) With the value of p and q found in (a), find the values of x, where graph f(x) cuts the x-axis.
(c) Hence, sketch the graph of f(x).
Solution:
(a)
(b)
(c)

Quadratic Functions, SPM Practice (Short Questions)
Question 3:
The straight line y = 5x – 1 does not intersect with the curve y = 2x2 + x + h.
Find the range of values of h.
Solution:
The straight line y = 5x – 1 does not intersect with the curve y = 2x2 + x + h.
Find the range of values of h.
Solution:
Question 4:
Find the maximum value of the function 5 – x – 2x2 , and the corresponding value of x.
Solution:
Find the maximum value of the function 5 – x – 2x2 , and the corresponding value of x.
Solution:
Quadratic Functions, SPM Practice (Short Questions)
Question 1:
Find the minimum value of the function f (x) = 2x2 + 6x + 5. State the value of xthat makes f (x) a minimum value.
Solution:
By completing the square for f (x) in the form of f (x) = a(x + p)2 + q to find the minimum value of f (x).
Since a = 2 > 0,
Therefore f (x) has a minimum value when . The minimum value of f (x) = ½.
Question 2:
The quadratic function f (x) = –x2 + 4x + k2, where k is a constant, has a maximum value of 8.
Find the possible values of k.
Solution:
f (x) = –x2 + 4x + k2
f (x) = –(x2 – 4x) + k2 ← [completing the square for f (x) in
the form of f (x) = a(x + p)2+ q]
f (x) = –[x2 – 4x + (–2)2 – (–2)2] + k2
f (x) = –[(x – 2)2 – 4] + k2
f (x) = –(x – 2)2 + 4 + k2
Given the maximum value is 8.
Therefore, 4 + k2 = 8
k2 = 4
k = ±2
3.4 Quadratic Inequalities (Part 2)
(C) Linear Inequality
Example 1
(a) Given , find the range of values of x for which y > 9 .
(b) Given , find the range of values of x for which y < 4 .

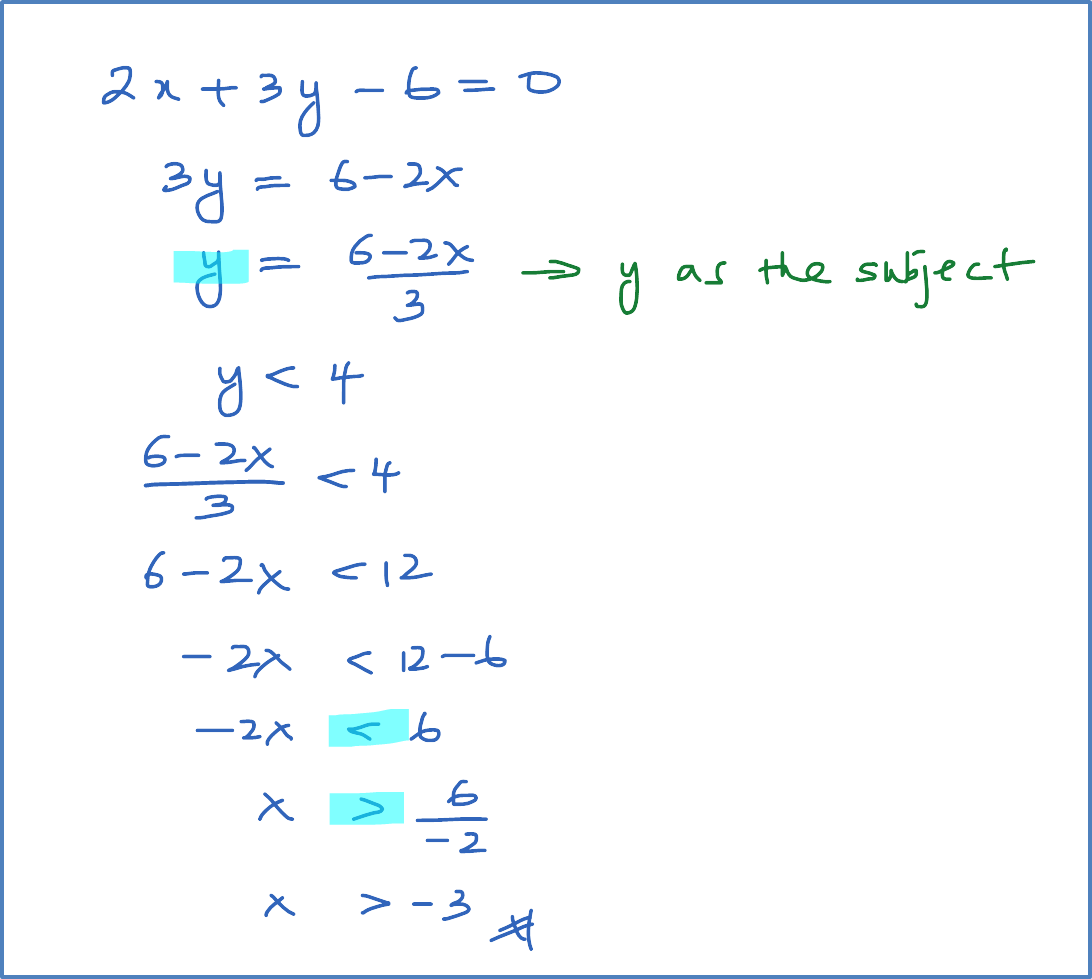
Example 1
(a) Given , find the range of values of x for which y > 9 .
(b) Given , find the range of values of x for which y < 4 .

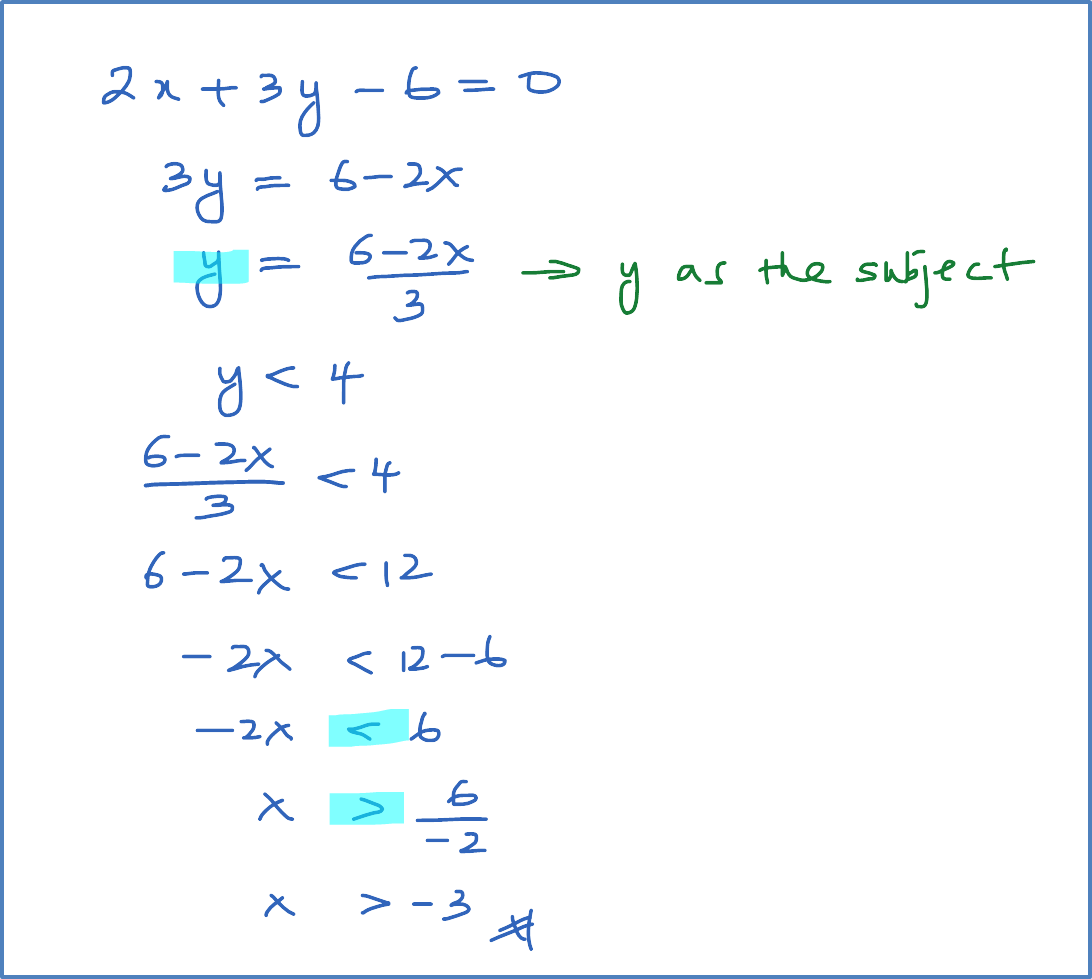
3.2 Maximum and Minimum Value of Quadratic Functions
Maximum and Minimum Point
- A quadratic functions can be expressed in the form by the method of completing the square.
- The minimum/maximum point can be determined from the equation in this form .
Minimum Point
- The quadratic function f(x) has a minimum value if a is positive.
- The quadratic function f(x) has a minimum value when (x + p) = 0
- The minimum value is equal to q.
- Hence the minimum point is (-p, q)
Maximum Point
- The quadratic function f(x) has a maximum value if a is negative.
- The quadratic function f(x) has a maximum value when (x + p) = 0
- The maximum value is equal to q.
- Hence the maximum point is (-p, q)
Example
Find the maximum or minimum point of the following quadratic equations
a.
b.
Answer:
(a)
(b)
Find the maximum or minimum point of the following quadratic equations
a.
b.
Answer:
(a)
(b)