3.3b Kesatuan Set
1. Kesatuan dua set, A dan B, diwakilkan sebagai A∪ B, ialah satu set yang unsur-unsurnya terdiri daripada semua unsur dalam set A atau set B atau kedua-dua set itu.
Gambar rajah Venn di bawah menunjukkan A∪ B:
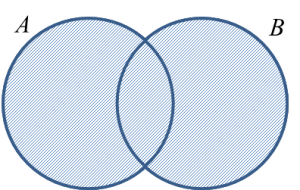
2. Kesatuan tiga set, A, B dan C, diwakilkan sebagai A∪ B ∪ C, ialah satu set yang unsur-unsurnya terdiri daripada semua unsur dalam set A, set B atau set C atau ketiga-tiga set itu.
Gambar rajah Venn di bawah menunjukkan A∪ B ∪ C:

Contoh 1:
Gambar rajah Venn di bawah menunjukkan bilangan unsur dalam set semesta, ξ, set P, set Q dan set R.


Diberi n(Q) = n(P∪ R)’, cari n (ξ).
Penyelesaian:
n(Q) = n(P∪ R)’
2x + 6 + 1 + 5 = 2x + 2x
2x + 12 = 4x
2x = 12
x = 6
n(ξ) = 2x + 2x + x + 7 + 6 + 1 + 5
= 5x + 19
= 5(6) + 19
= 30 + 19
= 49
Contoh 2:
Gambar rajah Venn di bawah menunjukkan set semesta, ξ = {Pelajar-pelajar tingkatan 3}, set A = {Pelajar-pelajar yang memain piano} dan set B = { Pelajar-pelajar yang memain biola}.


Diberi n (ξ) = 60, n (A) = 25, n (B) = 12 dan n (A ∩ B) = 8, cari bilangan pelajar yang tidak memain kedua-dua jenis alat muzik.
Penyelesaian:
Pelajar-pelajar yang tidak memain kedua-dua jenis alat muzik adalah diwakilkan oleh rantau berlorek, (A U B)’ di bawah.
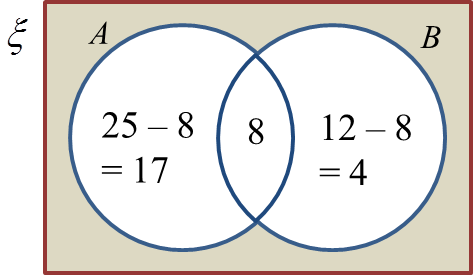
Bilangan pelajar yang tidak memain kedua-dua jenis alat muzik
= n (A∪ B)’
= 60 – 17 – 8 – 4
= 31