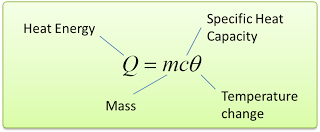
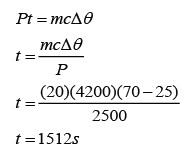- Specific heat capacity is a physical quantity used to compare the heat capacity of a given material of the same mass.
- It is the measure of how much energy can be store in 1 kg of mass of a substance.
- Specific heat capacity is defined as the amount of heat required to change the temperature of 1 kg of a substance by 1°C.
Mathematically, we write this as c = Q/mθ [Q = heat, c = specific heat capacity, m = mass, θ = change of temperature] - The SI unit of specific heat capacity is J/kg/°C.
- For example, the specific heat capacity of water is 4200 J/kg/°C means 4200J of heat energy is needed to change the temperature of 1kg water by 1°C.
- The amount of heat transferred in an object when temperature change can be calculated by using the following equation.
How much heat energy is required to change 2 kg of ice at 0°C into water at 20°C? [Specific latent heat of fusion of water = 334 000 J/kg; specific heat capacity of water = 4200 J/(kg K).]
Answer:
m = 2kg
Specific latent heat of fusion of water, L = 334 000 J/kg
specific heat capacity of water = 4200 J/(kg K)
Energy needed to melt 2kg of ice,
Q1 = mL = (2)(334000) = 668000J
Energy needed to change the temperature from 0°C to °C.
Q2 = mcθ = (2)(4200)(20 - 0) = 168000J
Total energy needed = Q1 + Q2 = 668000 + 168000 = 836000J
Starting at 20°C, how much heat is required to heat 0.3 kg of aluminum to its melting point and then to convert it all to liquid? [Specific heat capacity of aluminium = 900J kg-1 °C-1; Specific latent heat of aluminium = 321,000 Jkg-1, Melting point of aluminium = 660°C]
Answer:
m = 0.3kg
Specific latent heat of fusion of aluminium, L = 321 000 J/kg
specific heat capacity of aluminium = 900 J/(kg K)
Energy needed to increase the temperature from 20°C to 660°C
Q1 = mcθ = (0.3)(900)(660 - 20) = 172,800J
Energy needed to melt 0.3kg of aluminium,
Q2 = mL = (0.3)(321000) = 96,300J
Total energy needed = Q1 + Q2 = 172,800 + 96,300 = 269,100J
How much heat must be removed by a refrigerator from 2 kg of water at 70 °C to convert it to ice cubes at -11°C? [Specific heat capacity of water = 4200J kg-1 °C-1; Specific latent heat of fusion of ice = 334,000 Jkg-1, specific heat capacity of ice = 2100 J/(kg K)]
Answer:
m = 2kg
Specific latent heat of fusion of water, L = 334,000 J/kg
Specific heat capacity of water, cw = 4,200 J/(kg K)
Specific heat capacity of ice, ci = 2,100 J/(kg K)
Energy to be removed to reduce the temperature from 70°C to 0°C (Freezing point of water)
Q1 = mcθ = (2)(4200)(70 - 0) = 588,000J
Energy needed to freeze 2kg of water,
Q2 = mL = (2)(334,000) = 668,000J
Energy to be removed to reduce the temperature from 0°C to -11°C
Q3 = mcθ = (2)(2100)(0 - (-11)) = 46,200J
Total energy needed = Q1 + Q2 + Q3 = 588,000 + 668,000 = 46,200J = 1,302,200J
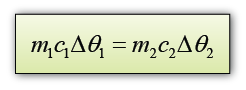
A 0.5 kg block of aluminium at a temperature of 100 °C is placed in 1.0 kg of water at 20 °C. Assuming that no thermal energy is lost to the surroundings, what will be the final temperature of the aluminium and water when they come to the same temperature? [The specific heat capacity of water is 4200 Jkg-1K-1 and The specific heat capacity of aluminium is 900 Jkg-1K-1]
Answer:
Let's say the final temperature for both aluminium block and water = θ
For aluminium,
m1 = 0.5 kg
c1 = 900 Jkg-1K-1
∆θ1 = 100 °C - θ
For water,
m2 = 1.0kg
c2 = 4200 Jkg-1K-1
∆θ2 = θ - 20 °C
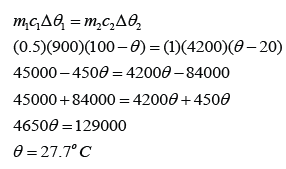
Example 2:
What will be the final temperature if 50 g of water at 0 °C is added to 250 g of water at 90 °C?
Answer:
For water at 90 °C,
m1 = 250g
c1 = c2 = c
∆θ1 = 90 °C - θ
For water at 0 °C,
m2 = 50g
∆θ2 = θ - 0 °C = θ
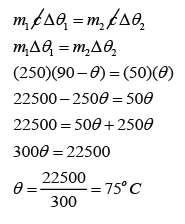
Example 3:
How much water at 10 °C is needed to cool 500 g of water at 90 °C down to 30 °C?
Answer:
For water at 90 °C,
m1 = 500g
c1 = c2 = c
∆θ1 = 90 - 30 = 60 °C
For water at 10 °C,
m2 = ?
∆θ2 = 30 - 10 = 20 °C
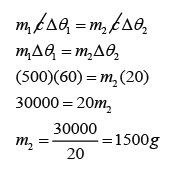
Conversion of Gravitational Energy to Thermal Energy
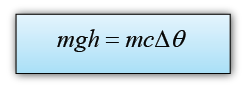
Example 1:
The Angel Falls in Venezuela is 979 m in height. Calculate the rise in temperature of the water when the water fall from the top to the bottom. (Assume that all the potential energy loss of the water is converted to heat) [The specific heat capacity of water is 4200Jkg-1K-1]
Answer:
The potential energy loss = mgh
The thermal energy gain of the water = mcθ
We assume that all the potential energy loss of the water is converted to heat, hence
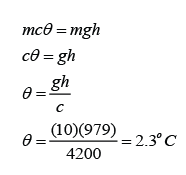
Example 2:
A mass m of lead shot is placed at the bottom of a vertical cardboard cylinder. The cylinder is 1.0 m long and closed at both ends. The cylinder is suddenly inverted so that the shot falls 1.0 m. By how much will the temperature of the shot increase if this process is repeated 200 times? Assume no heat loss to the surrounding. [The specific heat capacity of lead is 130Jkg-1K-1]
Answer:
Distance fall, h = 200 x 1m = 200m
Gratational field strength, g = 10 m/s²
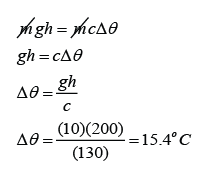
Conversion of Kinetic Energy to Thermal Energy
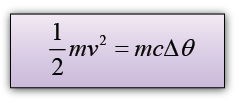
A 2.5g lead bullet is moving at 200 m/s when it strikes a wooden block and is brought to rest. If all the kinetic energy is transferred to thermal energy in the bullet, find the rise in temperature of the bullet. [The specific heat capacity of lead is 130Jkg-1K-1]
Answer:
v = 200m/s
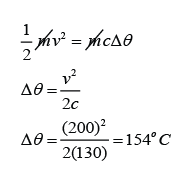
Conversion of Electrical Energy to Thermal Energy
Electrical energy, E = PtIf we assume that all the electrical energy convert into thermal energy, then
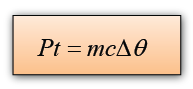
An electric heater supplies 2.5 kW of power in the form of heat to a tank of 0.02m³ of water. How long will it take to heat the water from 25 °C to 70 °C? Assume heat losses to the surroundings to be negligible. [Density of water = 1000kg/m³; The specific heat capacity of water is 4200Jkg-1K-1]
Answer:
P = 2500W
m = (0.02)(1000)=20kg
c = 4200Jkg-1K-1