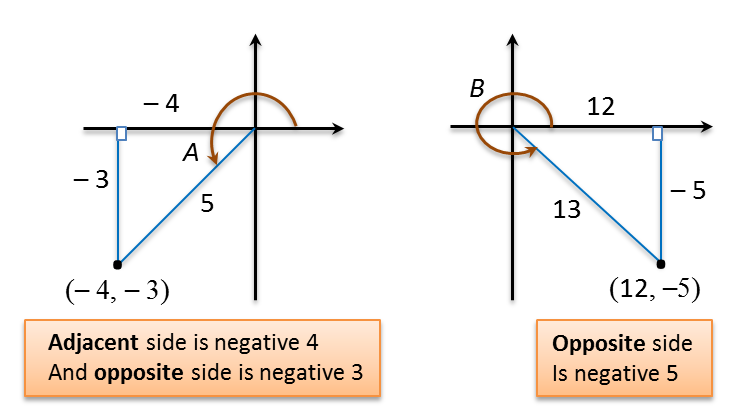
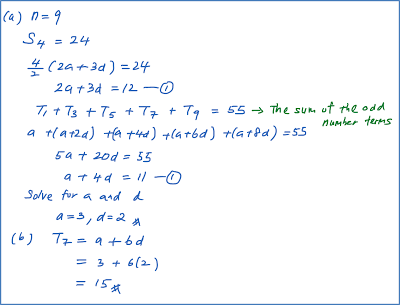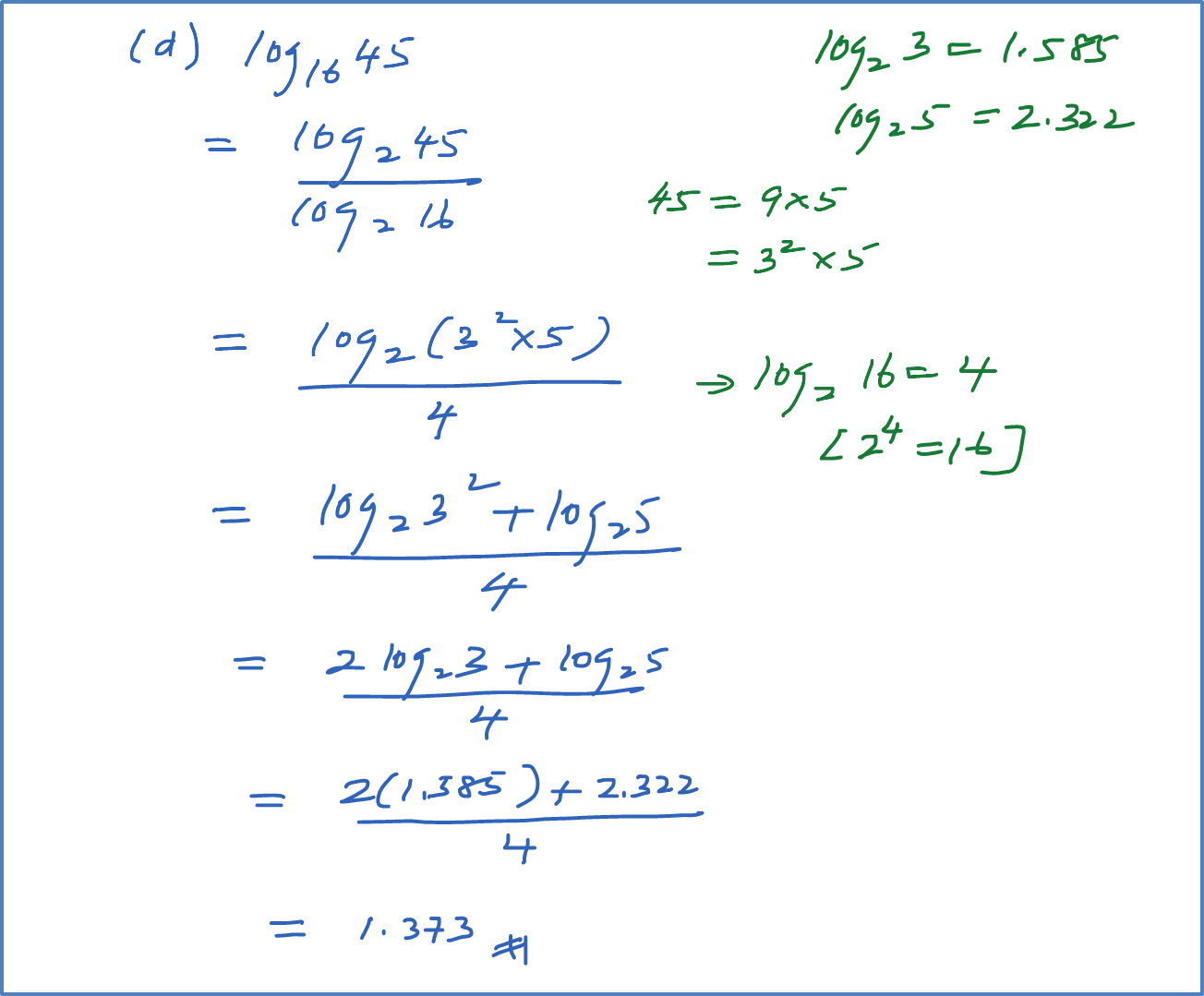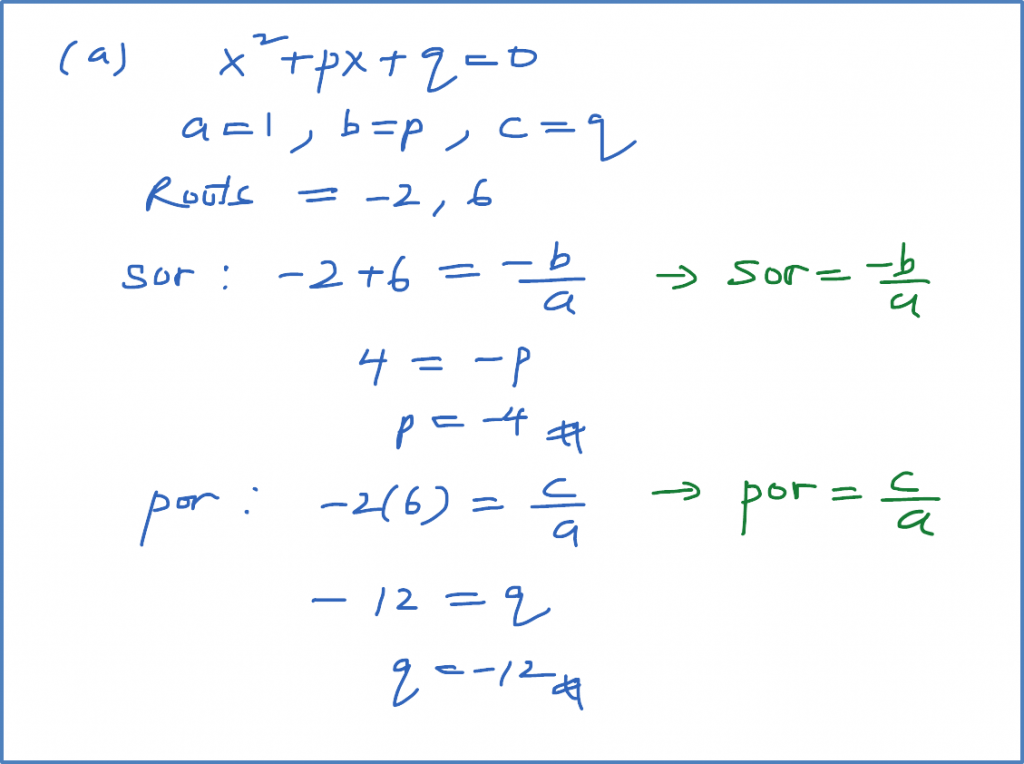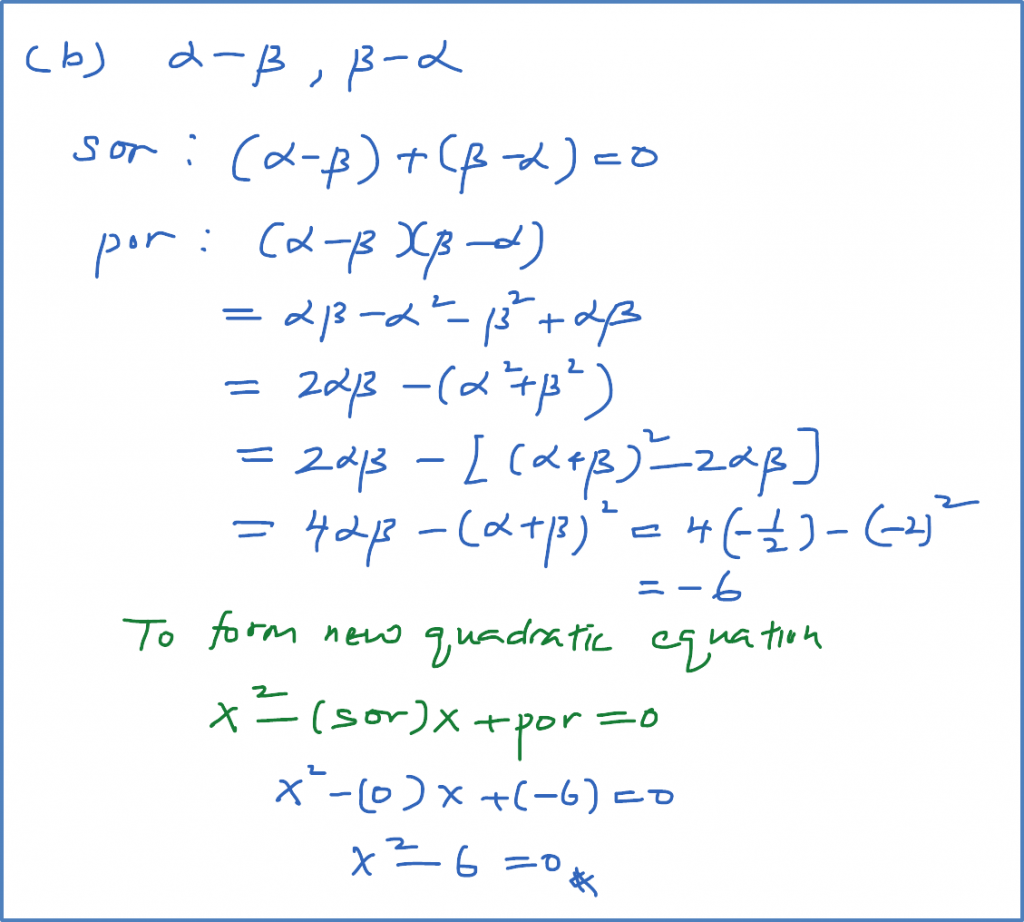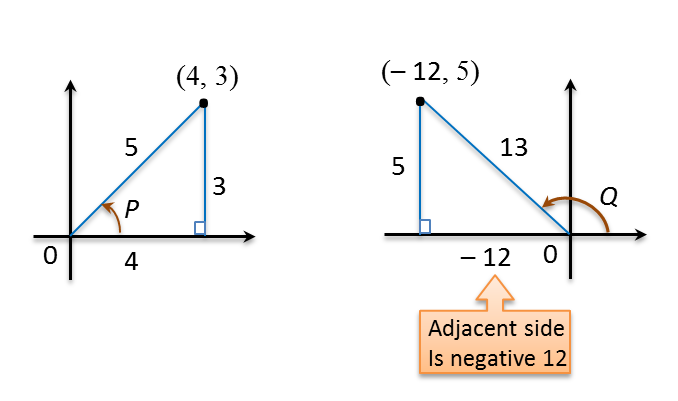Question 13:
An arithmetic progression consists of 10 terms. The sum of the last 5 terms is 5 and the fourth term is 9. Find the sum of this progression.
Solution:
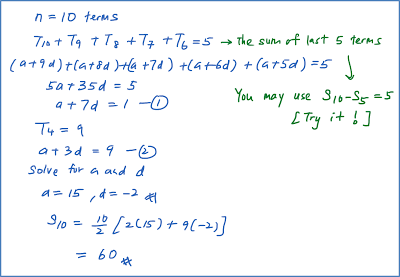
An arithmetic progression consists of 10 terms. The sum of the last 5 terms is 5 and the fourth term is 9. Find the sum of this progression.
Solution:
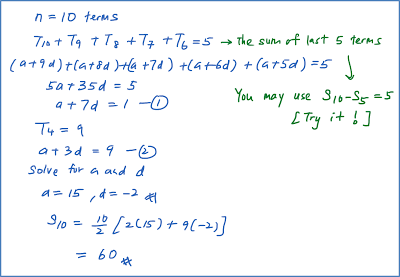
Question 14:
The sum of the first 6 terms of an arithmetic progression is 39 and the sum of the next 6 terms is –69. Find
(a) The first term and the common difference.
(b) The sum of all the terms from the 15th term to the 25th term.
Solution:


The sum of the first 6 terms of an arithmetic progression is 39 and the sum of the next 6 terms is –69. Find
(a) The first term and the common difference.
(b) The sum of all the terms from the 15th term to the 25th term.
Solution:


Question 15:
An arithmetic progression has 9 terms. The sum of the first four terms is 24 and the sum of all the odd number terms is 55. Find
(a) The first term and common difference,
(b) The seventh term.
Solution:
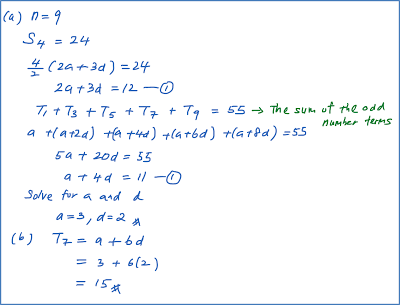
An arithmetic progression has 9 terms. The sum of the first four terms is 24 and the sum of all the odd number terms is 55. Find
(a) The first term and common difference,
(b) The seventh term.
Solution: