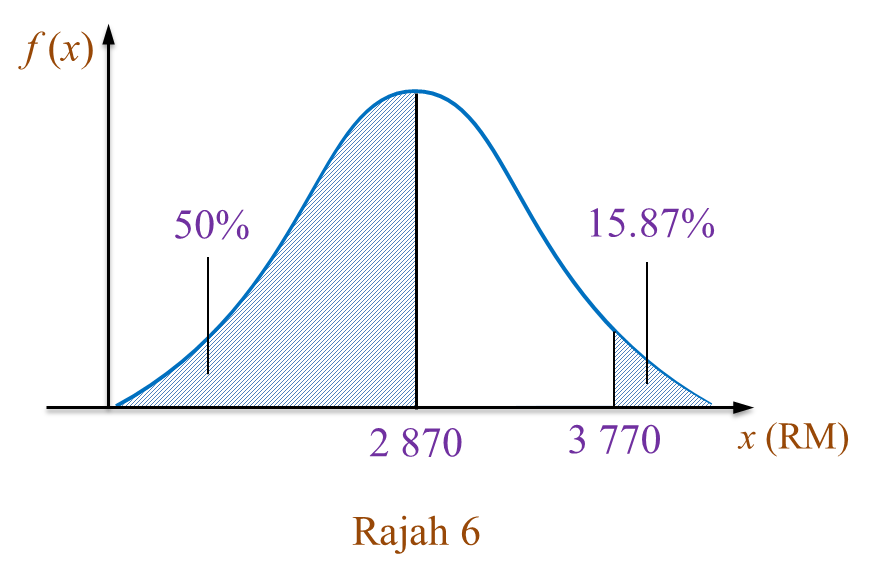
Soalan 9 (10 markah):
Penyelesaian secara lukisan berskala tidak diterima.
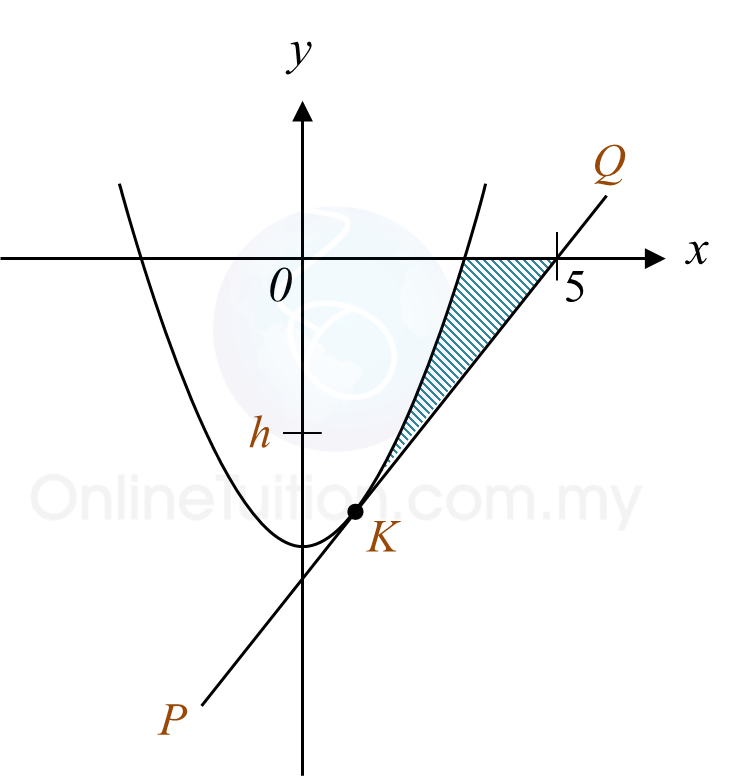
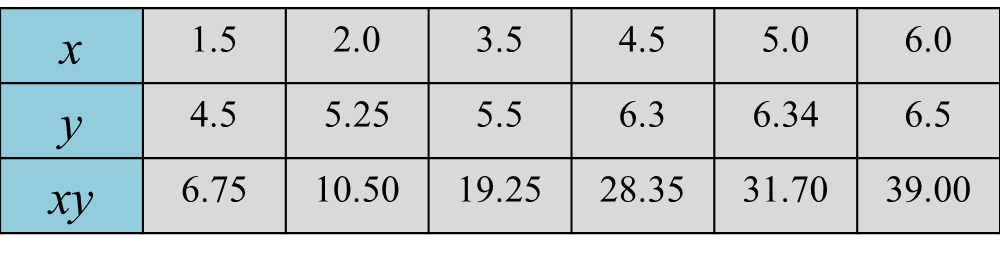
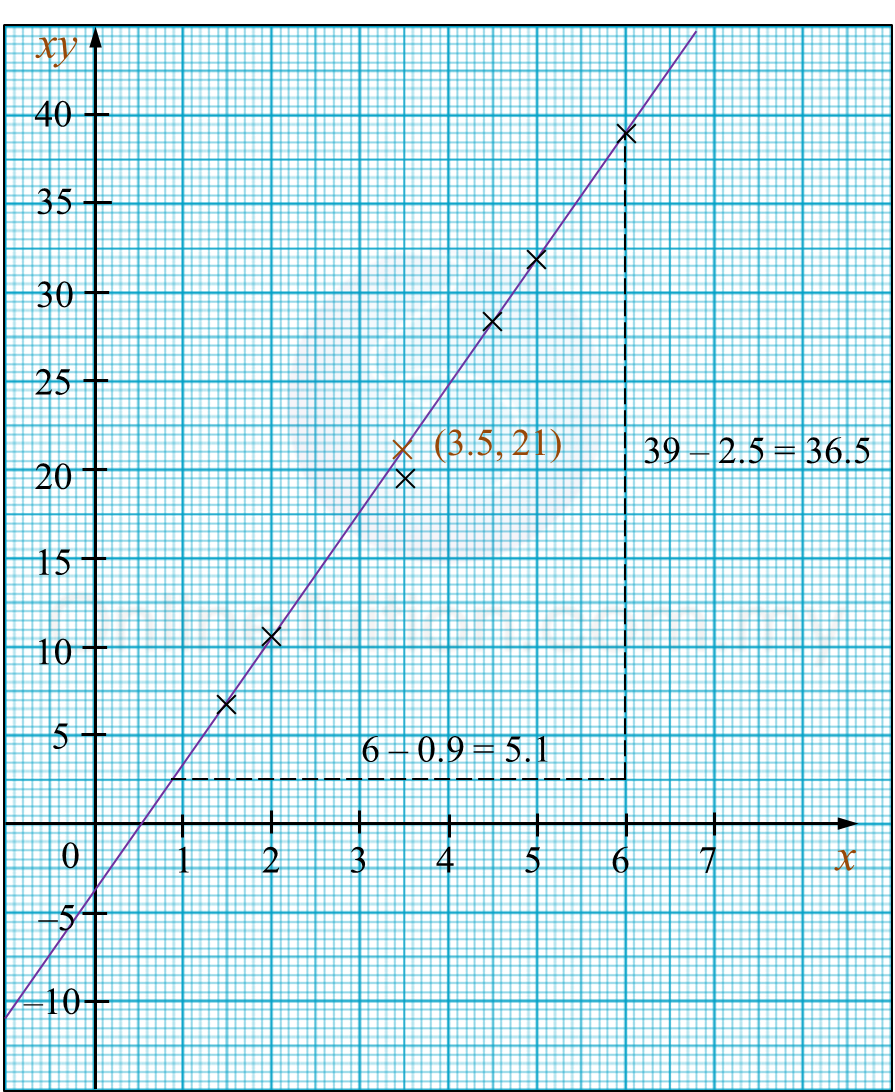
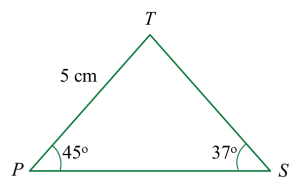
Rajah 8 menunjukkan prisma lutsinar dengan tapak PQRS berbentuk segi empat tepat. Permukaan condong PQUT ialah segi empat sama dengan sisi 12 cm dan permukaan condong RSTU ialah segi empat tepat. PTS ialah keratan rentas seragam bagi prisma itu. QST ialah satah berwarna hijau di dalam prisma itu.
 Diberi bahawa ∠PST = 37o dan ∠TPS = 45o.
Diberi bahawa ∠PST = 37o dan ∠TPS = 45o.
Cari
(a) panjang, dalam cm, bagi ST,
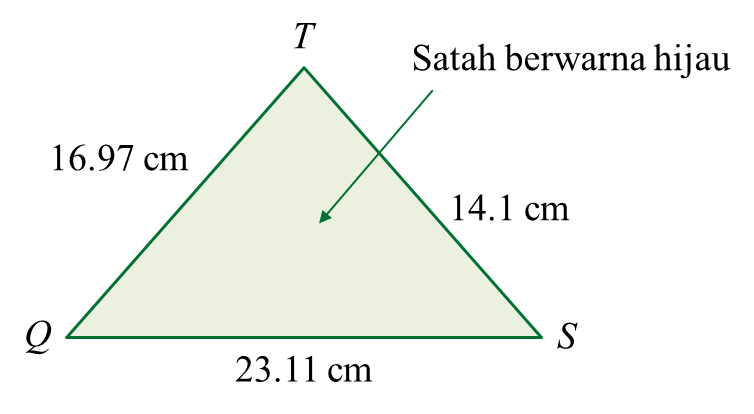
(b) luas, dalam cm2, satah berwarna hijau.
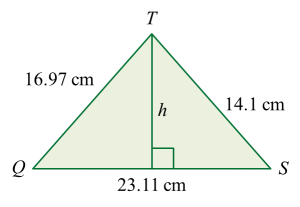
(c) panjang terdekat, dalam cm, dari titik T ke garis lurus QS.
Penyelesaian:
(a)
(b)
(c)
Penyelesaian secara lukisan berskala tidak diterima.
Rajah 8 menunjukkan prisma lutsinar dengan tapak PQRS berbentuk segi empat tepat. Permukaan condong PQUT ialah segi empat sama dengan sisi 12 cm dan permukaan condong RSTU ialah segi empat tepat. PTS ialah keratan rentas seragam bagi prisma itu. QST ialah satah berwarna hijau di dalam prisma itu.
 Diberi bahawa ∠PST = 37o dan ∠TPS = 45o.
Diberi bahawa ∠PST = 37o dan ∠TPS = 45o.Cari
(a) panjang, dalam cm, bagi ST,
(b) luas, dalam cm2, satah berwarna hijau.
(c) panjang terdekat, dalam cm, dari titik T ke garis lurus QS.
Penyelesaian:
(a)

(b)

(c)