Home › View all posts by user › Page 5

Author: user

4.6 Identity Matrix

Posted on by

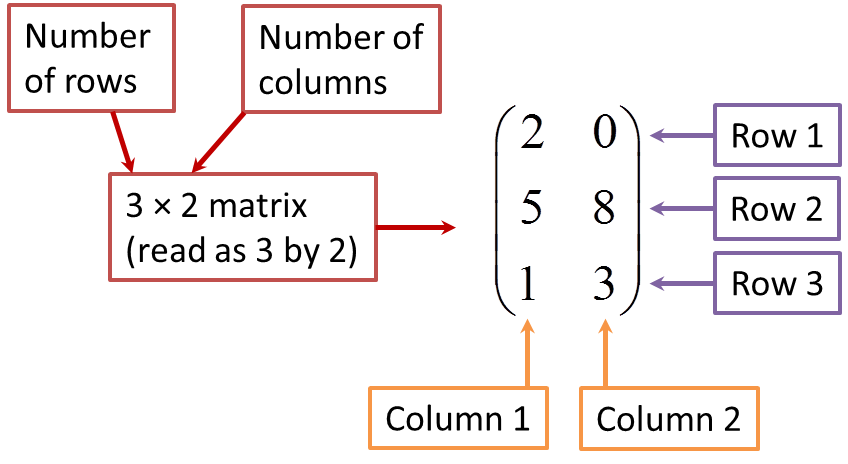
4.6 Identity Matrix
1. Identity matrix is a square matrix, usually denoted by the letter I and is also known as unit matrix.
 
2. All the diagonal elements (from top left to bottom right) of an identity matrix are 1 and the rest of the elements are 0.
For example,
( 1 0 0 1 )  and  ( 1 0       0 0 0 1       0 0      1 )  are identity matrices .

3. If I is the identity matrix of order n × n and A is a matrix of the same order, then IA = A and AI = A. 


Example 1:
Determine whether each of the following is an identity matrix of ( − 2 4 3 7 ) .
( a ) ( 1 0 0 1 ) ( b ) ( 0 1 1 0 )
 
Solution:
( a ) ( − 2 4 3 7 ) ( 1 0 0 1 ) = ( − 2 × 1 + 4 × 0 − 2 × 0 + 4 × 1 3 × 1 + 7 × 0 3 × 0 + 7 × 1 ) = ( − 2 4 3 7 ) Therefore, ( 1 0 0 1 ) is an identity matrix . ( b ) ( − 2 4 3 7 ) ( 0 1 1 0 ) = ( − 2 × 0 + 4 × 1 − 2 × 1 + 4 × 0 3 × 0 + 7 × 1 3 × 1 + 7 × 0 ) = ( 4 − 2 7 3 ) ≠ ( − 2 4 3 7 ) Therefore, ( 0 1 1 0 ) is not an identity matrix .  


Example 2:
Find the product of the following pairs of matrices and determine whether the given matrix is an identity matrix.

( a ) ( − 3 2 5 7 ) ( 1 0 0 1 ) and ( 1 0 0 1 ) ( − 3 2 5 7 ) ( b ) ( 0 0 1 1 ) ( 1 8 5 3 ) and ( 1 8 5 3 ) ( 0 0 1 1 )  
 
Solution:
( a ) ( − 3 2 5 7 ) ( 1 0 0 1 ) = ( − 3 × 1 + 2 × 0 − 3 × 0 + 2 × 1 5 × 1 + 7 × 0 5 × 0 + 7 × 1 ) = ( − 3 2 5 7 ) ( 1 0 0 1 ) ( − 3 2 5 7 ) = ( 1 × − 3 + 0 × 5 1 × 2 + 0 × 7 0 × − 3 + 1 × 5 0 × 2 + 1 × 7 ) = ( − 3 2 5 7 ) ∴ ( 1 0 0 1 ) is an identity matrix for ( − 3 2 5 7 ) . ( b ) ( 0 0 1 1 ) ( 1 8 5 3 ) = ( 0 × 1 + 0 × 5 0 × 8 + 0 × 3 1 × 1 + 1 × 5 1 × 8 + 1 × 3 ) = ( 0 0 6 11 ) ( 1 8 5 3 ) ( 0 0 1 1 ) = ( 1 × 0 + 8 × 1 1 × 0 + 8 × 1 5 × 0 + 3 × 1 5 × 0 + 3 × 1 ) = ( 8 8 3 3 ) ∴ ( 0 0 1 1 ) is NOT an identity matrix for ( 1 8 5 3 ) .

4.1 Matrix

Posted on by
4.1 Matrices
 
A matrix is a rectangular array of numbers enclosed in large brackets.
For example ( 2 0 3 1 ) is a matrix .
  
(A)   Rows, Columns and Order of Matrices
1. A matrix which has m rows and n columns is known as a matrix of order m × n.
 


2. A row matrix is a matrix which has only one row.
Example:
( 4 ),          ( 2     6 ),      ( 3     8    5 )  1 ×1         1 ×2          1 ×3           Only 1 row     
 
3. A column matrix is a matrix which has only one column.
Example:
( 3 ),           ( 2 6 ),         ( −5 7 −9 ) 1× 1        2× 1            3× 1              Only 1 column  
4. A square matrix is a matrix which has equal number of rows and columns.
Example:
( 3 ),         ( 7 0 2 5 ),       ( 1 3    9 0 6 4    1 3    5 ) 1×1           2×2                 3×3 Number of rows = Number of columns

4.2 Equal Matrices (Sample Questions)

Posted on by

Example 1:
State the values of the unknowns in the following pairs of equal matrix.
( 1 x + 2 4 − y − 1 ) = ( 1 3 2 − 1 )

Solution:
( 1 x + 2 4 − y − 1 ) = ( 1 3 2 − 1 )

x + 2 = 3
x = 1

4 – y = 2
–y = –2
y = 2


Example 2:
Calculate the values of p and q in each of the following matrix equations.
(a) ( 3 2 p + q p − 3 ) = ( 3 1 8 − 2 q − 3 ) (b) ( 10 0 5 p − 8 1 ) = ( p − 2 q 0 − 4 q 1 )

Solution:
(a) ( 3 2 p + q p − 3 ) = ( 3 1 8 − 2 q − 3 )

2p + q = 1
q = 1 – 2p ----(1)
p = 8 – 2q ----(2)

Substitute (1) into (2),
p = 8 – 2(1 – 2p)
p = 8 – 2 + 4p
p – 4p = 6
–3p = 6
p = –2

Substitute p = –2 into (1),
q = 1 – 2(–2)
q = 5


 (b) ( 10 0 5 p − 8 1 ) = ( p − 2 q 0 − 4 q 1 )

10 = p – 2q
p = 10 + 2q ----(1)
5p – 8 = –4q ----(2)

Substitute (1) into (2),
5 (10 + 2q) – 8 = –4q
50 + 10q – 8 = –4q
14q = –42
q = –3

Substitute q = –3 into (1),
p = 10 + 2(–3)
p = 4

4.3 Addition and Subtraction of Matrices

Posted on by

4.3 Addition and Subtraction of Matrices
 
(A) Determining whether addition or subtraction can be performed on two given matrices
1. Two matrices can be added or subtracted if both matrices have the same order.
2. The addition or subtraction of two matrices is performed by adding or subtracting the corresponding elements of the matrices.



Example 1:
State whether the following matrices can be added or subtracted. Give reason to your answer.
  (a)  ( 2 3 )  and  ( 1    8 ) (b)  ( 1 2 7 1 )  and  ( 10 0 − 3 − 1 )  
(c) (p   2   4) and (2   6   q)

Solution:
(a) Cannot because the matrices are not of the same order.
(b) Can because the matrices are of the same order.
(c) Can because the matrices are of the same order.


Example 2:
Express each of the following matrices as a single matrix.
If A=( 3 2 ) and B=( 5 1 ), then (a) A+B=( 3 2 )+( 5 1 ) =( 3+5 2+1 ) =( 8 3 )


( b ) B − A = ( 3 2 ) − ( 5 1 ) = ( 3 − 5 2 − 1 ) = ( − 2 1 )



4.2 Equal Matrices

Posted on by

4.2 Equal Matrices

(A) Determining whether two matrices are equal
1. Two matrices are equal if they have the same order and their corresponding elements are equal.
For example,  ( a b c d ) = ( e f g h )

Therefore, a = e, b = f, c = g and d = h.


Example 1:
Determine whether the following pairs of matrices are equal.
(a) A=( 10 8 −3 1 ) and B=( 10 8 −3 1 ) (b) P=( 2 −4 10 ) and Q=( 2 −3 10 ) (c) M=( 3 5 ) and N=( 4   7 )

Solution:
(a) Equal
(b) Not equal, because -4 ≠ -3.
(c) Not equal, because the orders of the matrices are not equal.




(B) Solving problem involving equal matrices
1. When matrices are equal, elements whose values are unknown can be determined.

Example 2:
State the value of the unknowns in the following pairs of equal matrix. 
( 2 x x + 2 y ) = ( − 8 10 )

Solution:
( 2 x x + 2 y ) = ( − 8 10 )

2x = -8
x = -4

x + 2y = 10
(-4) + 2y = 10
2y = 10 + 4
2y = 14
y = 7
 

4.3 Addition and Subtraction of Matrices (Sample Questions)

Posted on by

Example 1:
Find the addition of the following matrices.
(a)( 18   −7 )+( 3        6 ) (b) ( −13 0 7 −1 )+( −1 3 5 6 )

Solution:
(a) ( 18   −7 )+( 3       6 ) =( 18+3   −7+6 )=( 21   −1 ) (b) ( −13 0 7 −1 )+( −1 3 5 6 ) =( −13+( −1 ) 0+3 7+5 −1+6 )=( −14 3 12 5 )



Example 2:
Find the subtraction of the following matrices.
( a ) ( 9 6 ) − ( 7 − 2 ) ( b ) ( 3 − 4 0 5 ) − ( − 7 − 3 − 6 1 )

Solution:
( a ) ( 9 6 ) − ( 7 − 2 ) = ( 9 − 7 6 − ( − 2 ) ) = ( 2 8 ) ( b ) ( 3 − 4 0 5 ) − ( − 7 − 3 − 6 1 ) = ( 3 − ( − 7 ) − 4 − ( − 3 ) 0 − ( − 6 ) 5 − 1 ) = ( 3 + 7 − 4 + 3 0 + 6 5 − 1 ) = ( 10 − 1 6 4 )


Example 3:
Given that ( p q ) + ( 5 p 9 ) = ( − 12 3 q + 1 )  , find the values of p and q.

Solution:
( p q ) + ( 5 p 9 ) = ( − 12 3 q + 1 ) ( p + 5 p q + 9 ) = ( − 12 3 q + 1 )
 
p + 5p = –12
6p = –12
p = –2

q + 9 = 3q + 1
q – 3q = 1 – 9
–2q = –8
q = 4



Example 4:
Find the values of m and n in the following matrix equation.
( 7 6 n 1 ) − ( − 1 m − 4 − 2 ) = ( 5 12 6 11 )

Solution:
( 7 6 n 1 ) − ( − 1 m − 4 − 2 ) = ( 5 12 6 11 )

6 – m = 12
 –m = 6
 m = –6
n – (–4) = 6
n + 4 = 6
n = 2 

SPM Practice (Long Questions)

Posted on by

Further Practice:
Transformation III, Long Questions (Question 1)
 
Question 1:
(a) Transformation T is a translation ( − 4 2 ) and transformation P is an anticlockwise rotation of 90oabout the centre (1, 0).

State the coordinates of the image of point (5, 1) under each of the following transformation:
(i) Translation T,
(ii) Rotation P,
(iii) Combined transformation T2.

(b) Diagram below shows three quadrilaterals, ABCD, EFGH and JKLM, drawn on a Cartesian plane.
 
(i) JKLM is the image of ABCD under the combined transformation VW.
Describe in full the transformation:
(a) W   (b) V

(ii) It is given that quadrilateral ABCD represents a region of area 18 m2.
Calculate the area, in m2, of the region represented by the shaded region.
 
Solution:
(a)


(b)
 
(i)(a)
W: A reflection in the line x = –2
 
(i)(b)
V: An enlargement of scale factor 3 with centre (0, 4).
 
(b)(ii)
Area of EFGH = area of ABCD = 18 m2
Area of JKLM = (Scale factor)2 × Area of object
= 32 × area of EFGH
= 32 × 18
= 162 m2
Therefore,
Area of the shaded region
= Area of JKLM – area of EFGH
= 162 – 18
= 144 m2

SPM Practice (Long Questions)

Posted on by

Question 2:
(a) Diagram below shows point A and straight line y + x = 5 drawn on a Cartesian plane.


Transformation T is a translation (  5 −2 )
Transformation R is a reflection at the line y + x = 5.

State the coordinates of the image of point A under each of the following transformations:
(i) Transformation T,
(ii) Combined transformation TR.

(b) Diagram below shows pentagons JKLMN, PQRST and PUVWX, drawn on a Cartesian plane.

(i) PUVWX is the image of JKLMN under the combined transformation CB.
Describe in full the transformation:
(a) B    (b) C

(ii) It is given that pentagon JKLMN represents a region of area 80 m2 .
Calculate the area, in m2 , of the region represented by the shaded region.

Solution:
(a)

(i) (3, 4) → T → (8, 2)
(ii) (3, 4) → R → (1, 2) → T → (6, 0)

(b)

(b)(i)(a)
B: A clockwise rotation of  90o about the centre (0, 2).

(b)(i)(b)
Scale factor=PUPQ=64=32C: An enlargement of scale factor 32 with centre P(2,0)

(b)(ii)
Area of PQRST = Area of JKLMN
= 80 m2

Area of PUVWX=(32)2×area of PQRST=94×80=180 m2∴ Area of the shaded region= area of PUVWX−area of PQRST=180−80=100 m2

3.1 Combination of Two Transformations

Posted on by

3.1a Determining the image of an object under the combination of two isometric transformations
1. Translations, reflections and rotations are isometric transformations.
 
2. In an isometric transformation, the shape and the size of the image is the same as the object.
 
3. For two transformations, A and B,
(a) Combined transformation AB represents transformation B followed by transformation A.
(b) Combined transformation BA represents transformation A followed by transformation B.
(c) Combined transformation A2 = AA represents transformation A which is carried out twice consecutively.


3.1c Stating the Coordinates of the Image of a Point under a Combined Transformation

Posted on by

3.1c Stating the Coordinates of the Image of a Point under a Combined Transformation
 
1. The coordinates of the image of a point, K, under the combined transformation AB can be determined by the following steps.
 
Step 1:
Determine the coordinates of K’, the image of K, under the first transformation, B.

Step 2:
Determine the coordinates of K”, the image of K’, under the second transformation, A. K” is the image of K, under the combined transformation, AB.

Example:
T, P, R and E are four transformations that are defined as follows:
T = T r a n s l a t i o n ( − 4 3 )
P = Reflection in the y–axis.
R = Clockwise rotation 90o about the origin
E = Enlargement with scale factor of 3 and the origin as centre.
Find the coordinates of the image of the point A (3, –2) under each of the following combined transformation.
(a) TT (b) PT (c) ET (d) ER  (e) EP
 

Solution:
(a)


A(3, –2) → T → A’(–1, 1) → T → A”(–5, 4).


(b)


A(3, –2) → T → A’(–1, 1) → P → A”(1, 1).


(c)



A(3, –2) → T → A’(–1, 1) → E → A”( –3, 3).


(d)

A(3, –2) → R → A’(–2, 3) → E → A”( –6, –9).


(e)


A(3, –2) → P → A’(–3, –2) → E → A”( –9, –6).