Home › SPM Matematik Tambahan › Archive for Fungsi Kuadratik › Page 2

Fungsi Kuadratik

Bab 3 Fungsi Kuadratik

Posted on by
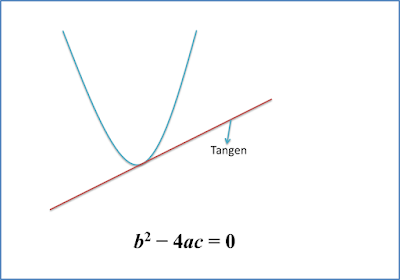
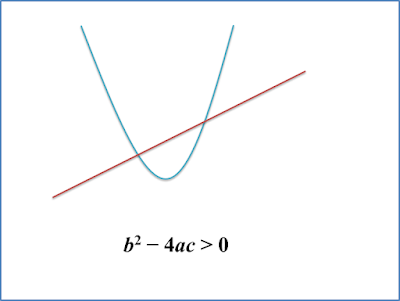
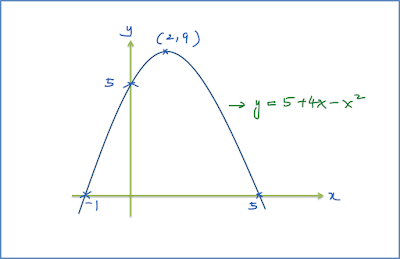
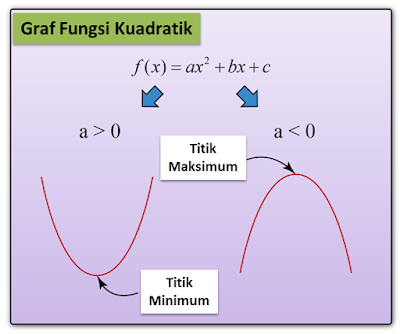
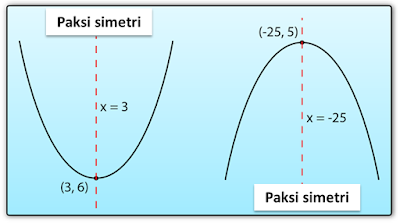
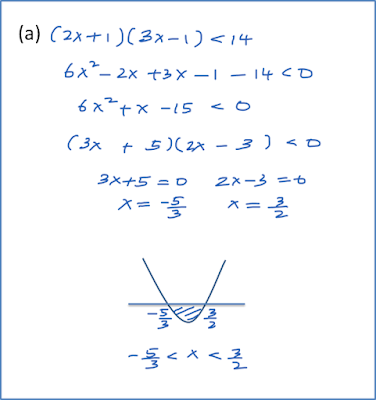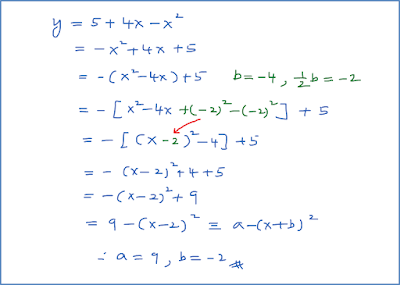3.5b Jenis Punca Persamaan Kuadratik (Contoh Soalan)

Contoh 2 (Garis Lurus Bersilang dengan Lengkung di Dua Titik Berlainan)
Garis lurus y = 2k+ 1 bersilang dengan  y=x+ k 2 x  di dua titik berlainan.  Cari julat nilai k.

Penyelesaian:




Contoh 3 (Garis Lurus Tidak Bersilang dengan Lengkung)
Cari julat nilai m dengan keadaan garis lurus y = mx+ 6 tidak bersilang dengan lengkung 2x2 – xy = 3.

Penyelesaian:




Bab 3 Fungsi Kuadratik

Posted on by
3.5a Jenis Punca Persamaan Kuadratik (Contoh Soalan)

Contoh 1 (Garis Lurus adalah Tangen kepada Lengkung)
Cari nilai p jika 8y= x + 2p adalah tangen kepada lengkung 2y2 = x+ p.


Penyelesaian:




Bab 3 Fungsi Kuadratik

Posted on by
3.5 Jenis Punca Persamaan Kuadratik
1.      Jenis punca persamaan kuadratik ax2  + bx + c= 0 ditentukan oleh nilai b2 − 4ac. Nilai b2 − 4ac memberi maklumat terhadap bilangan titik persilangan.

(a)  Apabila graf menyentuh garis lurus pada satu titik, iaitu terdapat hanya satu punca nyata bagi persamaan ax2  + bx + c = 0, maka b2  − 4ac = 0.




(b)  Apabila graf bersilang dengan garis lurus pada dua titik, iaitu terdapat dua punca nyata dan berbeza bagi persamaan ax2  + bx + c = 0, maka b2  − 4ac > 0.





(c)  Apabila graf tidak bersilang dengan garis lurus (tiada titik persilangan), iaitu tidak terdapat punca nyata bagi persamaan ax2  + bx + c = 0, maka b2  − 4ac < 0.



Bab 3 Fungsi Kuadratik

Posted on by
3.4 Ketaksamaan Kuadratik (Bahagian 2)

(C) Ketaksamaan Linear
Contoh 1:
(a) Diberi x= 6−y 3 , cari julat nilai x untuk y > 9.
(b) Diberi 2x + 3y – 6 = 0, cari julat nilai x untuk y < 4.

Penyelesaian:






(D) Ketaksamaan Kuadratik
Contoh 2:
Cari julat nilai x yang memuaskan setiap ketaksamaan kuadratik yang berikut:
(a) (2x+ 1) (3x – 1) < 14
(b) (x – 2) (5x – 4) + 1 > 0

Penyelesaian:





Bab 3 Fungsi Kuadratik

Posted on by
3.2c Cari Titik Maksimum atau Titik Minimum suatu Fungsi Kuadratik dengan Kaedah Penyempurnaan Kuasa Dua (Contoh Soalan)

Contoh:
Dengan menggunakan kaedah penyempurnaan kuasa dua, nyatakan nilai maksimum atau nilai minimum bagi setiap fungsi kuadratik yang berikut.
Seterusnya, cari titik maksimum atau titik minimum dan nyatakan paksi simetri yang sepadan.
(a) f (x ) = x 2 + 6x + 7
(b) f (x ) = 2x 2 – 6x + 7
(c) f (x ) = 5 – 2x – x 2
(d) f (x ) = 4 + 12x – 3x 2

Penyelesaian:









Bab 3 Fungsi Kuadratik

Posted on by

3.2.2 Cari Titik Maksimum atau Titik Minimum suatu Fungsi Kuadratik dengan Kaedah Penyempurnaan Kuasa Dua

Langkah-langkah untuk menukarkan bentuk am fungsi kuadratik kepada bentuk penyempurnaan kuasa dua:
Bentuk am fungsi kuadratik: f (x) = ax2 + bx + c 
Bentuk penyempurnaan kuasa dua: f (x) = a (x + p)2 + q.

Langkah 1: Pastikan pekali x2 adalah 1, dan lakukan pemfaktoran jika pekali x2 bukan 1.

Langkah 2: Tambah  +  ( pekali x 2 ) 2 − ( pekali x 2 ) 2

Langkah 3: Menyempurnakan kuasa dua [tukar  f (x) = ax2 + bx + c kepada f (x) = a (x + p)2+ q].


Bab 3 Fungsi Kuadratik

Posted on by
3.3a Lakaran Graf Fungsi Kuadratik (Contoh)

Contoh:
Ungkapkan y = 5 + 4x – x 2 dalam bentuk y = a – (x + b )2 , dengan a , b, dan c sebagai pemalar. Seterusnya, nyatakan nilai maksimum, y, dan nilai x. Lakarkan lengkung y = 5 + 4x – x 2 .

Penyelesaian:






Bab 3 Fungsi Kuadratik

Posted on by
3.3 Lakaran Graf Fungsi Kuadratik
Langkah-langkah melakar graf fungsi kuadratik f (x ) = ax 2 + bx + c adalah seperti berikut:
(a) Tentukan nilai a untuk mengetahui bentuk graf. 
(b) Cari titik maksimum/minimum graf
(c) Cari pintasan paksi-x graf
(d) Cari pintasan paksi-y graf


Contoh:
Lakar graf bagi fungsi kuadratik f (x ) = x 2 – x – 12

Penyelesaian:
(a) Bentuk graf
Pekali x2 adalah positif, maka graf adalah berbentuk parabola U dengan satu titik minimum.

(b) Titik minimum graf
Dengan penyempurnaan kuasa dua
f( x )= x 2 −x−12 f( x )= x 2 −x+ ( 1 2 ) 2 − ( 1 2 ) 2 −12 f( x )= ( x− 1 2 ) 2 − 1 4 −12 f( x )= ( x− 1 2 ) 2 −12 1 4 Titik minimum =( 1 2 ,−12 1 4 )

(c) Pintasan paksi-x, f (x ) = 0
 f (x ) = x 2 – x – 12
0 = x 2 – x – 12
(x + 5) (x – 6) = 0
x = – 5 atau x = 6

(d) ) Pintasan paksi-y, x = 0
 f (0) = (0)2 – (0) – 12 = – 12


Bab 3 Fungsi Kuadratik

Posted on by

3.2.1 Cari nilai maksimum/ minimum dan paksi simetri suatu fungsi
Contoh:
Nyatakan nilai maksimum atau nilai minimum bagi setiap fungsi kuadratik berikut dan nilai x yang sepadan.
Seterusnya, cari titik maksimum atau titik minimum dan nyatakan paksi simetri yang sepadan.
(a) f (x) = –2(x – 3)2 + 4
(b) f (x) = 3(x – 4)2 + 10
(c) f (x) = –3(x + 2)2 – 9
(d) f (x) = –8 + 2(x + 5)2

Penyelesaian:




Bab 3 Fungsi Kuadratik

Posted on by
3.1b Graf Fungsi Kuadratik
1.      Graf fungsi kuadratik berbentuk parabola.
2.      Apabila pekali bagi x2 ialah positif, a > 0, graf adalah parabola berbentuk U .
3.      Apabila pekali bagi x2 ialah negative, a < 0, graf adalah parabola berbentuk ∩.



(A) Paksi simetri
Paksi simetri adalah satu garis tegak lurus yang melalui titik maksimum atau titik minimum graf parabola.