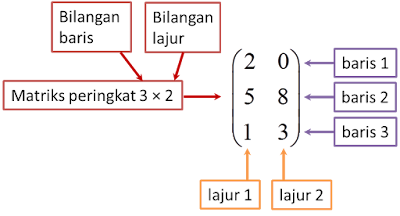
4.10.6 Matriks, SPM Praktis (Soalan Panjang)

Posted on May 12, 2020 by Myhometuition

Soalan 11 (5 markah):
Semasa hari sukan sekolah, murid menggunakan kupon untuk membeli makanan dan minuman.
Ali dan Larry masing-masing telah membelanjakan RM31 dan RM27. Ali membeli 2 kupon makanan dan 5 kupon minuman manakala Larry membeli 3 kupon makanan dan 1 kupon minuman.
Menggunakan kaedah matriks, hitung harga, dalam RM, bagi satu kupon makanan dan bagi satu kupon minuman.

Penyelesaian:
Ali membelanjakan RM31. Dia membeli 2 kupon makanan dan 5 kupon minuman.
Larry membelanjakan RM27. Dia membeli 3 kupon makanan dan 1 kupon minuman.
x = Harga bagi satu kupon makanan
y = Harga bagi satu kupon minuman

$\begin{array}{l} (\begin{array}{l} 25 \\ 3 1 \end{array}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 31 \\ 27 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{2 (1) - 5 (3)} (\begin{array}{l} 1 - 5 \\ - 32 \end{array}) (\begin{array}{l} 31 \\ 27 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{2 - 15} (\begin{array}{l} 1 (31) + (- 5) (27) \\ - 3 (31) + 2 (27) \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 13} (\begin{array}{l} - 104 \\ - 39 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 8 \\ 3 \end{array}) \\ x = 8 dan y = 3 \\ Maka, harga bagi satu kupon makanan \\ ialah RM8 dan harga bagi satu kupon \\ minuman ialah RM3 . \end{array}$

Soalan 12 (5 markah):
Jadual menunjukkan maklumat pembelian buku oleh Maslinda.

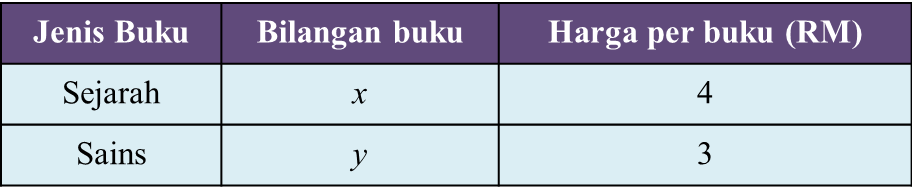Jadual

Maslinda membeli x buah buku Sejarah dan y buah buku Sains. Jumlah buku yang dibeli ialah 5. Jumlah harga untuk buku yang dibeli ialah RM17.

(a) Tulis dua persamaan linear dalam sebutan x dan y untuk mewakili maklumat di atas.

(b) Seterusnya, dengan menggunakan kaedah matriks, hitung nilai x dan nilai y.

Penyelesaian:
(a)
x + y = 5
4x + 3y = 17

(b)

$\begin{array}{l} (\begin{array}{l} 1 1 \\ 4 3 \end{array}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 5 \\ 17 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{1 (3) - 4 (1)} (\begin{array}{l} 3 - 1 \\ - 41 \end{array}) (\begin{array}{l} 5 \\ 17 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = - 1 (\begin{array}{l} 3 (5) + (- 1) (17) \\ - 4 (5) + (1) (17) \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = - 1 (\begin{array}{l} 15 - 17 \\ - 20 + 17 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = - 1 (\begin{array}{l} - 2 \\ - 3 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 2 \\ 3 \end{array}) \\ x = 2 dan y = 3 \end{array}$

4.10.5 Matriks, SPM Praktis (Soalan Panjang)

Posted on May 11, 2020 by Myhometuition

Soalan 9:

$(a) Diberi \frac{1}{s} (\begin{matrix} - 4 & 2 \\ - 5 & 3 \end{matrix}) (\begin{matrix} t & - 2 \\ 5 & - 4 \end{matrix}) = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}), cari nilai s dan nilai t .$

(b) Menggunakan kaedah matriks, hitung nilai x dan nilai y yang memuaskan persamaan matriks berikut:

$(\begin{matrix} - 4 & 2 \\ - 5 & 3 \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 1 \\ 2 \end{array})$

Penyelesaian:

$\begin{array}{l} (a) \\ \frac{1}{s} (\begin{matrix} t & - 2 \\ 5 & - 4 \end{matrix}) = {(\begin{matrix} - 4 & 2 \\ - 5 & 3 \end{matrix})}^{- 1} \\ = \frac{1}{(- 4) (3) - (2) (- 5)} (\begin{matrix} 3 & - 2 \\ 5 & - 4 \end{matrix}) \\ = \frac{1}{- 2} (\begin{matrix} 3 & - 2 \\ 5 & - 4 \end{matrix}) \\ ∴ s = - 2, t = 3 \end{array}$

$\begin{array}{l} (b) \\ (\begin{matrix} - 4 & 2 \\ - 5 & 3 \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 1 \\ 2 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 2} (\begin{matrix} 3 & - 2 \\ 5 & - 4 \end{matrix}) (\begin{array}{l} 1 \\ 2 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 2} (\begin{array}{l} (3) (1) + (- 2) (2) \\ (5) (1) + (- 4) (2) \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 2} (\begin{array}{l} - 1 \\ - 3 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} \frac{1}{2} \\ \frac{3}{2} \end{array}) \\ ∴ x = \frac{1}{2}, y = \frac{3}{2} \end{array}$

Soalan 10 (6 markah):

$\begin{array}{l} Diberi A = (\begin{array}{l} 4 - 2 \\ 3 - 1 \end{array}), B = m (\begin{array}{l} - 1 n \\ - 3 4 \end{array}) \\ dan I = (\begin{array}{l} 1 0 \\ 01 \end{array}) . \end{array}$
(a) Cari nilai m dan nilai n jika AB = I.
(b) Tulis persamaan linear serentak berikut dalam bentuk persamaan matriks:
4x – 2y = 3
3x – y = 2
Seterusnya, menggunakan kaedah matriks, hitung nilai x dan nilai y.

Penyelesaian:
(a)

$\begin{array}{l} Jika A B = I, maka B = A^{- 1} \\ A^{- 1} = \frac{1}{4 (- 1) - (- 2) (3)} (\begin{array}{l} - 1 2 \\ - 34 \end{array}) \\ A^{- 1} = \frac{1}{2} (\begin{array}{l} - 1 2 \\ - 34 \end{array}) \\ Secara perbandingan: \\ B = A^{- 1} \\ m (\begin{array}{l} - 1 n \\ - 3 4 \end{array}) = \frac{1}{2} (\begin{array}{l} - 1 2 \\ - 34 \end{array}) \\ m = \frac{1}{2}; n = 2 \end{array}$

(b)

$\begin{array}{l} 4 x - 2 y = 3 \\ 3 x - y = 2 \\ (\begin{array}{l} 4 - 2 \\ 3 - 1 \end{array}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 3 \\ 2 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{2} (\begin{array}{l} - 1 2 \\ - 34 \end{array}) (\begin{array}{l} 3 \\ 2 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{2} (\begin{array}{l} (- 1) (3) + (2) (2) \\ (- 3) (3) + (4) (2) \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{2} (\begin{array}{l} 1 \\ - 1 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} \frac{1}{2} \\ - \frac{1}{2} \end{array}) \\ x = \frac{1}{2} dan y = - \frac{1}{2} \end{array}$

4.10.4 Matriks, SPM Praktis (Soalan Panjang)

Posted on May 11, 2020 by Myhometuition

Soalan 7:

$(a) Cari matriks songsang bagi (\begin{matrix} 3 & 2 \\ 5 & 4 \end{matrix}) .$
(b) Ethan dan Rahman pergi ke pasar raya untuk membeli kiwi dan jambu. Ethan membeli 3 biji kiwi dan 2 biji jambu dengan harga RM9. Rahman membeli 5 biji kiwi dan 4 biji jambu dengan harga RM16.
Dengan menggunakan kaedah matriks, cari harga, dalam RM, bagi sebiji kiwi dan sebiji jambu.

Penyelesaian:

$\begin{array}{l} (a) \\ Matriks songsang bagi (\begin{matrix} 3 & 2 \\ 5 & 4 \end{matrix}) \\ = \frac{1}{12 - 10} (\begin{matrix} 4 & - 2 \\ - 5 & 3 \end{matrix}) \\ = \frac{1}{2} (\begin{matrix} 4 & - 2 \\ - 5 & 3 \end{matrix}) \\ = (\begin{matrix} 2 & - 1 \\ - \frac{5}{2} & \frac{3}{2} \end{matrix}) \end{array}$

$\begin{array}{l} (b) \\ 3 x + 2 y = 9................. (1) \\ 5 x + 4 y = 16............... (2) \\ (\begin{matrix} 3 & 2 \\ 5 & 4 \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 9 \\ 16 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{matrix} 2 & - 1 \\ - \frac{5}{2} & \frac{3}{2} \end{matrix}) (\begin{array}{l} 9 \\ 16 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} (2) (9) + (- 1) (16) \\ (- \frac{5}{2}) (9) + (\frac{3}{2}) (16) \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 18 - 16 \\ - \frac{45}{2} + 24 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 2 \\ \frac{3}{2} \end{array}) \\ x = 2, y = \frac{3}{2} \\ ∴ Harga bagi sebiji kiwi = RM2 \\ Harga bagi sebiji jambu = RM1 .50 \end{array}$

Soalan 8:
Matriks songsang bagi

$(\begin{matrix} 4 & - 1 \\ 2 & 5 \end{matrix}) ialah t (\begin{matrix} 5 & 1 \\ - 2 & n \end{matrix}) .$
(a) Cari nilai n dan nilai t.
(b) Tulis persamaan linear serentak berikut dalam persamaan matriks:
4x – y = 7
2x + 5y = –2
Seterusnya, menggunakan kaedah matriks, hitung nilai x dan nilai y.

[adinserter block="3"]
Penyelesaian:

$\begin{array}{l} (a) \\ t (\begin{matrix} 5 & 1 \\ - 2 & n \end{matrix}) = {(\begin{matrix} 4 & - 1 \\ 2 & 5 \end{matrix})}^{- 1} \\ = \frac{1}{(4) (5) - (- 1) (2)} (\begin{matrix} 5 & 1 \\ - 2 & 4 \end{matrix}) \\ = \frac{1}{22} (\begin{matrix} 5 & 1 \\ - 2 & 4 \end{matrix}) \\ ∴ t = \frac{1}{22}, n = 4 \end{array}$

$\begin{array}{l} (b) \\ (\begin{matrix} 4 & - 1 \\ 2 & 5 \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 7 \\ - 2 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{22} (\begin{matrix} 5 & 1 \\ - 2 & 4 \end{matrix}) (\begin{array}{l} 7 \\ - 2 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{22} (\begin{array}{l} (5) (7) + 1 (- 2) \\ (- 2) (7) + (4) (- 2) \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{22} (\begin{array}{l} 35 - 2 \\ - 14 - 8 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{22} (\begin{array}{l} 33 \\ - 22 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} \frac{3}{2} \\ - 1 \end{array}) \\ ∴ x = \frac{3}{2}, y = - 1 \end{array}$

4.10.3 Matriks, SPM Praktis (Soalan Panjang)

Posted on May 11, 2020 by Myhometuition

Soalan 5:

$(a) Diberi \frac{1}{14} (\begin{matrix} 2 & s \\ - 4 & t \end{matrix}) (\begin{matrix} t & - 1 \\ 4 & 2 \end{matrix}) = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}), cari nilai s dan nilai t .$
(b) Tulis persamaan linear serentak berikut dalam bentuk matriks:
3x – 2y = 5
9x + y = 1
Seterusnya, menggunakan kaedah matriks, hitung nilai x dan nilai y.

Penyelesaian:

$\begin{array}{l} (a) \\ \frac{1}{14} (\begin{matrix} 2 & s \\ - 4 & t \end{matrix}) (\begin{matrix} t & - 1 \\ 4 & 2 \end{matrix}) = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) \\ \frac{1}{14} (\begin{matrix} 2 t + 4 s & - 2 + 2 s \\ - 4 t + 4 t & 4 + 2 t \end{matrix}) = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) \\ \frac{- 2 + 2 s}{14} = 0 \\ 2 s = 2 \\ s = 1 \\ \frac{4 + 2 t}{14} = 1 \\ 4 + 2 t = 14 \\ 2 t = 10 \\ t = 5 \end{array}$

$\begin{array}{l} (b) \\ (\begin{matrix} 3 & - 2 \\ 9 & 1 \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} 5 \\ 1 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{21} (\begin{matrix} 1 & 2 \\ - 9 & 3 \end{matrix}) (\begin{array}{l} 5 \\ 1 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{21} (\begin{array}{l} (1) (5) + (2) (1) \\ (- 9) (5) + (3) (1) \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{21} (\begin{array}{l} 7 \\ - 42 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} \frac{1}{3} \\ - 2 \end{array}) \\ ∴ x = \frac{1}{3}, y = - 2 \end{array}$

Soalan 6:

$\begin{array}{l} Diberi bahawa matriks P = (\begin{matrix} 6 & - 3 \\ - 5 & 2 \end{matrix}) dan matriks Q = \frac{1}{m} (\begin{matrix} 2 & 3 \\ 5 & n \end{matrix}) \\ dengan keadaan P Q = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) . \end{array}$
(a) Cari nilai m dan nilai n.
(b) Tulis persamaan linear serentak berikut dalam bentuk matriks:
6x – 3y = –24
–5x + 2y = 18
Seterusnya, menggunakan kaedah matriks, hitung nilai x dan nilai y.

Penyelesaian:

$\begin{array}{l} (a) \\ m = 6 (2) - (- 3) (- 5) \\ = 12 - 15 \\ m = - 3 \\ n = 6 \end{array}$

$\begin{array}{l} (b) \\ (\begin{matrix} 6 & - 3 \\ - 5 & 2 \end{matrix}) (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} - 24 \\ 18 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{12 - 15} (\begin{matrix} 2 & 3 \\ 5 & 6 \end{matrix}) (\begin{array}{l} - 24 \\ 18 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 3} (\begin{array}{l} (2) (- 24) + (3) (18) \\ (5) (- 24) + (6) (18) \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = \frac{1}{- 3} (\begin{array}{l} 6 \\ - 12 \end{array}) \\ (\begin{array}{l} x \\ y \end{array}) = (\begin{array}{l} - 2 \\ 4 \end{array}) \\ ∴ x = - 2, y = 4 \end{array}$

Bab 15 Matriks

Posted on October 13, 2016 by user

4.9 SPM Practis (Kertas 1)

Soalan 5:

Diberi bahawa

$(3 x) (\begin{array}{l} x \\ - 1 \end{array}) = (18),$ cari nilai x.

Penyelesaian:

$(3 x) (\begin{array}{l} x \\ - 1 \end{array}) = (18)$

[3 × x + x (–1)] = (18)

3x – x = 18

2x = 18

x = 9

Soalan 6:

$(\begin{matrix} 3 & 4 \\ - 2 & 3 \end{matrix}) (\begin{array}{l} 5 \\ - 2 \end{array}) =$

Penyelesaian:

$\begin{array}{l} (\begin{matrix} 3 & 4 \\ - 2 & 3 \end{matrix}) (\begin{array}{l} 5 \\ - 2 \end{array}) = (\begin{array}{l} (3) (5) + (4) (- 2) \\ (- 2) (5) + (3) (- 2) \end{array}) \\ = (\begin{array}{l} 15 - 8 \\ - 10 - 6 \end{array}) \\ = (\begin{array}{l} 7 \\ - 16 \end{array}) \end{array}$

Soalan 7:

$(\begin{matrix} 2 & 4 \\ \begin{array}{l} - 3 \\ 4 \end{array} & \begin{array}{l} 0 \\ 1 \end{array} \end{matrix}) (\begin{array}{l} 1 \\ - 3 \end{array}) =$

Penyelesaian:

Peringkat hasil darab dua matriks

$= (3 \times 2) (2 \times 1) = (3 \times 1)$

$\begin{array}{l} (\begin{matrix} 2 & 4 \\ \begin{array}{l} - 3 \\ 4 \end{array} & \begin{array}{l} 0 \\ 1 \end{array} \end{matrix}) (\begin{array}{l} 1 \\ - 3 \end{array}) = (\begin{array}{l} 2 (1) + 4 (- 3) \\ (- 3) (1) + 0 (- 3) \\ (4) (1) + 1 (- 3) \end{array}) \\ = (\begin{array}{l} 2 - 12 \\ - 3 + 0 \\ 4 - 3 \end{array}) \\ = (\begin{array}{l} - 10 \\ - 3 \\ 1 \end{array}) \end{array}$

Soalan 8:

$(1 - 1 2) (\begin{matrix} 5 & 1 \\ \begin{array}{l} - 3 \\ 2 \end{array} & \begin{array}{l} 0 \\ 4 \end{array} \end{matrix}) =$

Penyelesaian:

Peringkat hasil darab dua matriks

$= (1 \times 3) (3 \times 2) = (1 \times 2)$

$(1 - 1 2) (\begin{matrix} 5 & 1 \\ \begin{array}{l} - 3 \\ 2 \end{array} & \begin{array}{l} 0 \\ 4 \end{array} \end{matrix}) =$

= (1×5 + (–1)(–3) + (2)(2) 1×1 + (–1)(0) + (2)(4))

= (5 + 3 + 4 1 + 0 + 8)

= (12 9)

Bab 15 Matriks

Posted on May 9, 2016 by user

4.7 Matriks Songsang

1. Jika A ialah satu matriks segi empat sama, dan B ialah satu lagi matriks segi empat sama, dan A × B = B × A = I, maka matriks A adalah matriks songsang bagi matriks B dan sebaliknya.

2. Matriks songsang bagi A ditulis sebagai A^-1.

3. Matriks songsang hanya wujud bagi matriks segi empat sama, tetapi bukan semua matriks segi empat sama mempunyai matriks songsang.

4. Jika AB ≠ I atau BA ≠ I, maka A bukan matriks songsang bagi B dan Bbukan matriks songsang bagi A.

Contoh 1:

Tentukan sama ada matriks

$A = (\begin{matrix} 2 & 9 \\ 1 & 5 \end{matrix})$ ialah matriks songsang bagi matriks

$B = (\begin{matrix} 5 & - 9 \\ - 1 & 2 \end{matrix}) .$

Penyelesaian:

$\begin{array}{l} A B = (\begin{matrix} 2 & 9 \\ 1 & 5 \end{matrix}) (\begin{matrix} 5 & - 9 \\ - 1 & 2 \end{matrix}) \\ = (\begin{matrix} 2 \times 5 + 9 \times - 1 & 2 \times - 9 + 9 \times 2 \\ 1 \times 5 + 5 \times - 1 & 1 \times - 9 + 5 \times 2 \end{matrix}) \\ = (\begin{matrix} 10 + (- 9) & - 18 + 18 \\ 5 + (- 5) & - 9 + 10 \end{matrix}) \\ = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) = I \end{array}$

$\begin{array}{l} A B = (\begin{matrix} 5 & - 9 \\ - 1 & 2 \end{matrix}) (\begin{matrix} 2 & 9 \\ 1 & 5 \end{matrix}) \\ = (\begin{matrix} 5 \times 2 + (- 9) \times 1 & 5 \times 9 + (- 9) \times 5 \\ - 1 \times 2 + 2 \times 1 & - 1 \times 9 + 2 \times 5 \end{matrix}) \\ = (\begin{matrix} 10 + (- 9) & 18 - 18 \\ - 2 + 2 & - 9 + 10 \end{matrix}) \\ = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) = I \end{array}$

AB = BA = I

Maka A ialah matriks songsang bagi matriks B dan sebaliknya.

5. Matriks songsang bagi suatu matriks boleh dicari melalui rumus.

Jika

$A = (\begin{matrix} a & b \\ c & d \end{matrix})$ , maka matriks songsang bagi A, A^-1, diberi melalui rumus yang berikut.

$A^{- 1} = \frac{1}{a d - b c} (\begin{matrix} d & - b \\ - c & a \end{matrix}), dan a d - b c \neq 0$

6. ad – bc dikenali sebagai penentu bagi matriks A.

7. Jika penentu adalah sifar, ad – bc = 0, maka A^-1, tidak wujud.

Contoh 2:

Cari matriks songsang bagi

$A = (\begin{matrix} 6 & 1 \\ - 9 & - 1 \end{matrix})$ dengan menggunakan rumus.

Penyelesaian:

$\begin{array}{l} A = (\begin{matrix} 6 & 1 \\ - 9 & - 1 \end{matrix}) \\ a = 6, b = 1, c = - 9, d = - 1 \\ A^{- 1} = \frac{1}{a d - b c} (\begin{matrix} d & - b \\ - c & a \end{matrix}) \\ A^{- 1} = \frac{1}{6 \times - 1 - (1 \times - 9)} (\begin{matrix} - 1 & - 1 \\ 9 & 6 \end{matrix}) \\ A^{- 1} = \frac{1}{- 6 + 9} (\begin{matrix} - 1 & - 1 \\ 9 & 6 \end{matrix}) \\ A^{- 1} = \frac{1}{3} (\begin{matrix} - 1 & - 1 \\ 9 & 6 \end{matrix}) = (\begin{matrix} - \frac{1}{3} & - \frac{1}{3} \\ 3 & 2 \end{matrix}) \end{array}$

Contoh 3:

Matriks songsang bagi

$(\begin{matrix} - 7 & 2 \\ - 9 & 2 \end{matrix}) ialah r (\begin{matrix} 2 & s \\ 9 & t \end{matrix}) .$ Cari nilai bagi r, sdan t.

Penyelesaian:

$\begin{array}{l} Let A = (\begin{matrix} - 7 & 2 \\ - 9 & 2 \end{matrix}) \\ A^{- 1} = \frac{1}{- 7 \times 2 - (- 9) \times 2} (\begin{matrix} 2 & - 2 \\ 9 & - 7 \end{matrix}) \\ A^{- 1} = \frac{1}{4} (\begin{matrix} 2 & - 2 \\ 9 & - 7 \end{matrix}) \\ ∴ r (\begin{matrix} 2 & s \\ 9 & t \end{matrix}) = \frac{1}{4} (\begin{matrix} 2 & - 2 \\ 9 & - 7 \end{matrix}) \\ Dengan perbandingan, \\ r = \frac{1}{4}, s = - 2, t = - 7. \end{array}$

Bab 15 Matriks

Posted on May 8, 2016 by user

4.6 Matriks Identiti

1. Matriks identiti ialah suatu matriks segi empat sama. Ia biasanya diwakili oleh huruf I .

2. Matriks identity berperingkat 2 × 2 dan 3 × 3 adalah

$(\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) dan (\begin{matrix} 1 & 00 \\ \begin{array}{l} 0 \\ 0 \end{array} & \begin{array}{l} 10 \\ 01 \end{array} \end{matrix}) .$

3. Jika Iialah matriks identity n × n dan Aialah matriks yang berperingkat sama, maka IA = A dan AI = A.

Contoh 1:

Tentukan sama ada setiap matriks yang berikut adalah matriks identity bagi

$(\begin{matrix} - 2 & 4 \\ 3 & 7 \end{matrix}) .$

$(a) (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) (b) (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix})$

Penyelesaian:

$\begin{array}{l} (a) (\begin{matrix} - 2 & 4 \\ 3 & 7 \end{matrix}) (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) \\ = (\begin{matrix} - 2 \times 1 + 4 \times 0 & - 2 \times 0 + 4 \times 1 \\ 3 \times 1 + 7 \times 0 & 3 \times 0 + 7 \times 1 \end{matrix}) \\ = (\begin{matrix} - 2 & 4 \\ 3 & 7 \end{matrix}) \\ Maka, (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) ialah satu matriks identiti . \end{array}$

$\begin{array}{l} (b) (\begin{matrix} - 2 & 4 \\ 3 & 7 \end{matrix}) (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) \\ = (\begin{matrix} - 2 \times 0 + 4 \times 1 & - 2 \times 1 + 4 \times 0 \\ 3 \times 0 + 7 \times 1 & 3 \times 1 + 7 \times 0 \end{matrix}) \\ = (\begin{matrix} 4 & - 2 \\ 7 & 3 \end{matrix}) \\ \neq (\begin{matrix} - 2 & 4 \\ 3 & 7 \end{matrix}) \\ Maka, (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) bukan satu matriks identiti . \end{array}$

Contoh 2:

Cari hasil darab bagi setiap pasangan matriks yang berikut dan tentukan sama ada matriks yang diberi merupakan matriks identity atau tidak.

$\begin{array}{l} (a) (\begin{matrix} - 3 & 2 \\ 5 & 7 \end{matrix}) (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) dan (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) (\begin{matrix} - 3 & 2 \\ 5 & 7 \end{matrix}) \\ (b) (\begin{matrix} 0 & 0 \\ 1 & 1 \end{matrix}) (\begin{matrix} 1 & 8 \\ 5 & 3 \end{matrix}) dan (\begin{matrix} 1 & 8 \\ 5 & 3 \end{matrix}) (\begin{matrix} 0 & 0 \\ 1 & 1 \end{matrix}) \end{array}$

Penyelesaian:

$\begin{array}{l} (a) \\ (\begin{matrix} - 3 & 2 \\ 5 & 7 \end{matrix}) (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) \\ = (\begin{matrix} - 3 \times 1 + 2 \times 0 & - 3 \times 0 + 2 \times 1 \\ 5 \times 1 + 7 \times 0 & 5 \times 0 + 7 \times 1 \end{matrix}) = (\begin{matrix} - 3 & 2 \\ 5 & 7 \end{matrix}) \\ (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) (\begin{matrix} - 3 & 2 \\ 5 & 7 \end{matrix}) \\ = (\begin{matrix} 1 \times - 3 + 0 \times 5 & 1 \times 2 + 0 \times 7 \\ 0 \times - 3 + 1 \times 5 & 0 \times 2 + 1 \times 7 \end{matrix}) = (\begin{matrix} - 3 & 2 \\ 5 & 7 \end{matrix}) \\ ∴ (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) ialah matriks identiti bagi (\begin{matrix} - 3 & 2 \\ 5 & 7 \end{matrix}) . \end{array}$

$\begin{array}{l} (b) \\ (\begin{matrix} 0 & 0 \\ 1 & 1 \end{matrix}) (\begin{matrix} 1 & 8 \\ 5 & 3 \end{matrix}) \\ = (\begin{matrix} 0 \times 1 + 0 \times 5 & 0 \times 8 + 0 \times 3 \\ 1 \times 1 + 1 \times 5 & 1 \times 8 + 1 \times 3 \end{matrix}) = (\begin{matrix} 0 & 0 \\ 6 & 11 \end{matrix}) \\ (\begin{matrix} 1 & 8 \\ 5 & 3 \end{matrix}) (\begin{matrix} 0 & 0 \\ 1 & 1 \end{matrix}) \\ = (\begin{matrix} 1 \times 0 + 8 \times 1 & 1 \times 0 + 8 \times 1 \\ 5 \times 0 + 3 \times 1 & 5 \times 0 + 3 \times 1 \end{matrix}) = (\begin{matrix} 8 & 8 \\ 3 & 3 \end{matrix}) \\ ∴ (\begin{matrix} 0 & 0 \\ 1 & 1 \end{matrix}) BUKAN matriks identiti bagi (\begin{matrix} 1 & 8 \\ 5 & 3 \end{matrix}) . \end{array}$

Bab 15 Matriks

Posted on May 8, 2016 by user

4.2 Matriks Sama

(A) Menentukan sama ada dua matriks adalah sama

1. Dua matriks yang sama mempunyai peringkat yang sama dan setiap unsur sepadannya adalah juga sama.

Misalnya,

$(\begin{matrix} a & b \\ c & d \end{matrix}) = (\begin{matrix} e & f \\ g & h \end{matrix})$

Maka, a = e, b = f, c = g dan d = h.

Contoh 1:

Tentukan sama ada setiap pasangan matriks yang berikut adalah sama atau tidak.

$\begin{array}{l} (a) A = (\begin{matrix} 10 & 8 \\ - 3 & 1 \end{matrix}) dan B = (\begin{matrix} 10 & 8 \\ - 3 & 1 \end{matrix}) \\ (b) P = (\begin{array}{l} 2 \\ - 4 \\ 10 \end{array}) dan Q = (\begin{array}{l} 2 \\ - 3 \\ 10 \end{array}) \\ (c) M = (\begin{array}{l} 3 \\ 5 \end{array}) dan N = (4 7) \end{array}$

Penyelesaian:

(a) Sama

(b) Tidak sama, kerana unsur-unsur sepadan tidak sama. -4 tidak sama dengan -3.

(B) Menyelesaikan masalah yang melibatkan matriks sama

1. Nilai unsur yang tidak diketahui dalam dua matriks yang sama boleh ditentukan dengan menyamakan unsur-unsur yang sepadan.

Contoh 2:

Cari nilai anu dalam pasangan matriks sama yang berikut.

$(\begin{array}{l} 2 x \\ x + 2 y \end{array}) = (\begin{array}{l} - 8 \\ 10 \end{array})$

Penyelesaian:

$\begin{array}{l} (\begin{array}{l} 2 x \\ x + 2 y \end{array}) = (\begin{array}{l} - 8 \\ 10 \end{array}) \\ 2 x = - 8 \\ x = - 4 \\ x + 2 y = 10 \\ - 4 + 2 y = 10 \\ 2 y = 14 \\ y = 7 \end{array}$

Bab 15 Matriks

Posted on May 7, 2016 by user

4.1 Matriks

1. Matriksialah nombor-nombor yang disusun dalam baris dan lajur untuk membentuk satu tatasusunan segi empat tepat.

2. Matriks pada umumnya ditulis dalam tanda kurungan.

Misalnya,

$(\begin{matrix} 2 & 0 \\ 3 & 1 \end{matrix})$ ialah suatu matriks.

(A) Menentukan billangan baris, bilangan lajur dan peringkat, sesuatu matriks

1. Matriks yang mempunyai mbaris dan n lajurs dikenali sebagai matriks peringkat
m × n.

2. Matriks baris ialah suatu matriks yang mempunyai hanya satu baris sahaja.

Misalnya:

$\begin{array}{l} (4), (2 6), (3 8 5) \\ 1 \times 1 1 \times 2 1 \times 3 \\ ↖ ↑ ↗ \\ Hanya satu baris \end{array}$

3. Matriks lajur ialah suatu matriks yang mempunyai hanya satu lajur sahaja.

Misalnya:

$\begin{array}{l} (3), (\begin{array}{l} 2 \\ 6 \end{array}), (\begin{array}{l} - 5 \\ 7 \\ - 9 \end{array}) \\ 1 \times 12 \times 13 \times 1 \\ ↖ ↑ ↗ \\ Hanya satu lajur \end{array}$

4. Matriks segi empat sama ialah suatu matriks yang mempunyai bilangan baris dan bilangan lajur yang sama.
Misalnya:

$\begin{array}{l} (3), (\begin{matrix} 7 & 0 \\ 2 & 5 \end{matrix}), (\begin{matrix} 1 & 39 \\ \begin{array}{l} 0 \\ 6 \end{array} & \begin{array}{l} 41 \\ 35 \end{array} \end{matrix}) \\ 1 \times 12 \times 23 \times 3 \\ ↖ ↑ ↗ \\ Bilangan baris = Bilangan lajur \end{array}$

Bab 15 Matriks

Posted on May 7, 2016 by user

4.3 Penambahan dan Penolakan Matriks

(A) Mengenal Pasti Dua Matriks yang boleh ditambah atau ditolak

1. Dua matriks boleh ditambah atau ditolak jika kedua-dua matriks itu mempunyai peringkat yang sama.

2. Penambahan atau penolakan dua matriks yang sama peringkat ialah pembentukan satu matriks yang unsur-unsurnya merupakan hasil tambah (atau hasil tolak) unsur-unsur sepadan dalam dua matriks itu.

Contoh 1:

Tentukan sama ada pasangan matriks yang berikut boleh ditambah atau ditolak. Memberi sebab untuk jawapan anda.

$\begin{array}{l} (a) (\begin{array}{l} 2 \\ 3 \end{array}) dan (1 8) \\ (b) (\begin{matrix} 1 & 2 \\ 7 & 1 \end{matrix}) dan (\begin{matrix} 10 & 0 \\ - 3 & - 1 \end{matrix}) \\ (c) (p 2 4) dan (2 6 q) \end{array}$

Penyelesaian:

(a) Tidak boleh ditambah atau ditolak kerana peringkat dua matriks itu tidak sama.

(b) Boleh ditambah atau ditolak kerana peringkat dua matriks adalah sama.

(c) Boleh ditambah atau ditolak kerana peringkat dua matriks adalah sama.

Contoh 2:

Ungkapkan setiap yang berikut sebagai satu matriks tunggal.

$\begin{array}{l} Diberi A = (\begin{array}{l} 3 \\ 2 \end{array}) dan B = (\begin{array}{l} 5 \\ 1 \end{array}), cari \\ (a) A + B, \\ (b) B - A \end{array}$

Penyelesaian:

$\begin{array}{l} (a) A + B = (\begin{array}{l} 3 \\ 2 \end{array}) + (\begin{array}{l} 5 \\ 1 \end{array}) \\ = (\begin{array}{l} 3 + 5 \\ 2 + 1 \end{array}) \\ = (\begin{array}{l} 8 \\ 3 \end{array}) \end{array}$

$\begin{array}{l} (b) B - A = (\begin{array}{l} 3 \\ 2 \end{array}) - (\begin{array}{l} 5 \\ 1 \end{array}) \\ = (\begin{array}{l} 3 - 5 \\ 2 - 1 \end{array}) \\ = (\begin{array}{l} - 2 \\ 1 \end{array}) \end{array}$