5.1 Ubahan Langsung (Bahagian 1)
(A) Menentukan sama ada suatu kuantiti berubah secara langsung terhadap kuantiti yang lain
1.
Jika suatu kuantiti y berubah secara langsung dengan suatu kuantiti x,
(a)
y bertambah apabila x bertambah
(b)
y berkurung apabila x berkurung
2.
Suatu kuantiti y berubah secara langsung dengan suatu kuantiti x jika dan hanya jika yx=k
di mana k ialah pemalar.
3.
yberubah secara langsung dengan x ditulis aebagai y α x.
4.
Apabila y α x, maka graf y melawan x adalah satu garis lurusyang melalui asalan.
(B) Ungkapkan suatu ubahan langsung dalam bentuk persamaan yang melibatkan dua pemboleh ubah
Contoh 1:
Diberi bahawa yberubah secara langsung dengan x dan y = 20 apabila x = 36. Tulis ubahan langsung itu dalam bentuk persamaan.
Penyelesaian:
y∝xy=kx20=k(36)k=2036=49→(Cari k terdahulu)∴
(C) Mencari nilai bagi suatu pemboleh ubah dalam ubahan langsung
Jika y berubah secara langsung dengan x dan maklumat yang mencukupi diberi, maka nilai y atau x dapat dicari dengan menggunakan
Contoh 2:
Diberi bahawa yberubah secara langsung dengan x dan y = 24 apabila x = 8, cari
(a)
Persamaan yang mengaitkan y kapada x
(b)
nilai bagi y apabila x = 6
(c)
nilai bagi x apabila y = 36
Penyelesaian:
Kaedah 1: Guna y = kx
(a)
yα x
y= kx
Apabila y= 24, x = 8
24 = k (8)
k = 3
(b)
Apabila x= 6,
y = 3(6)
y
= 18



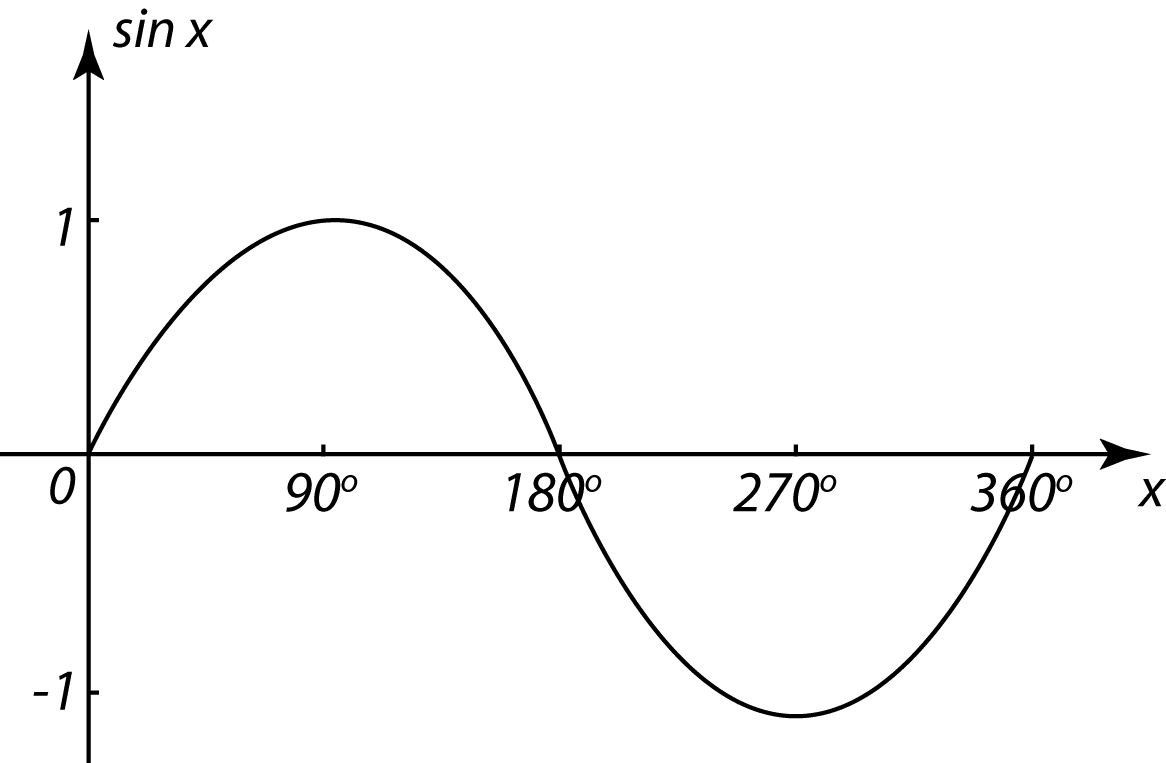
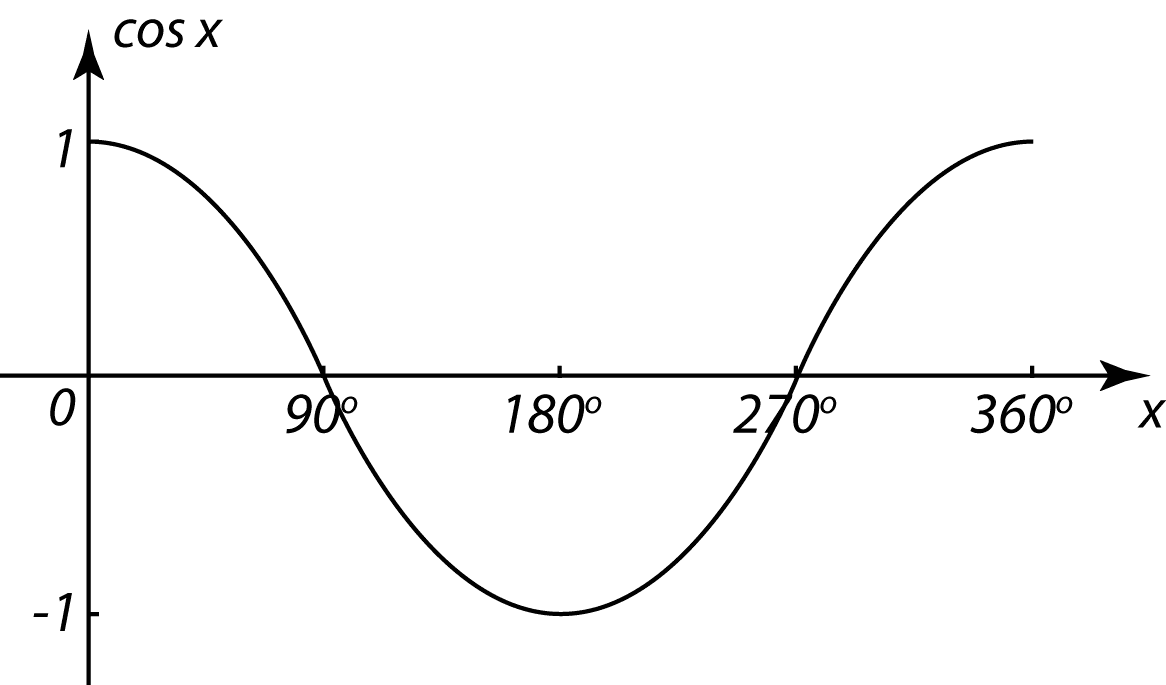
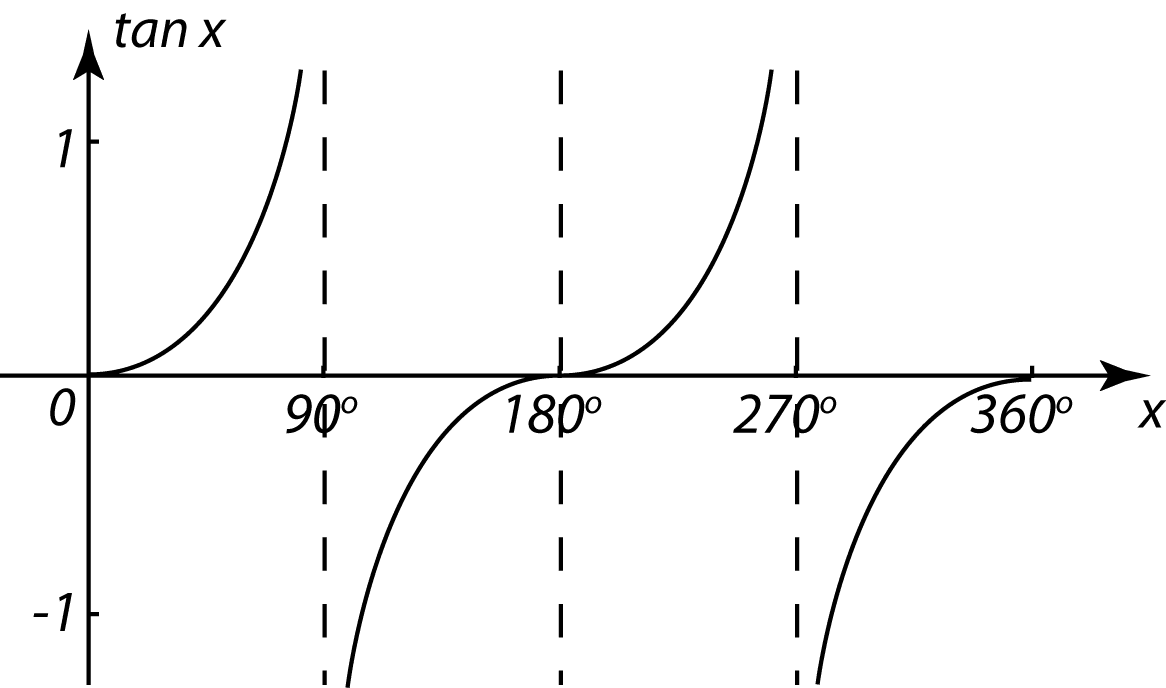
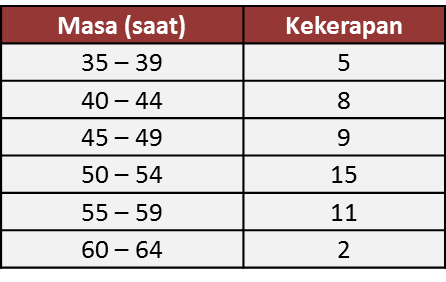
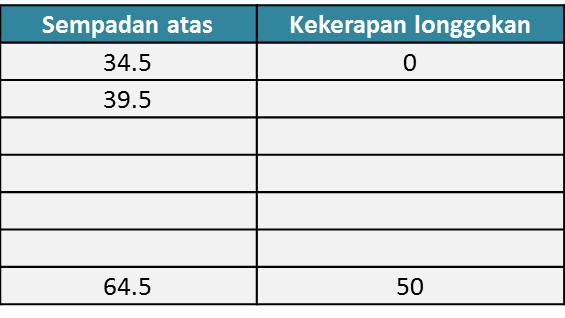
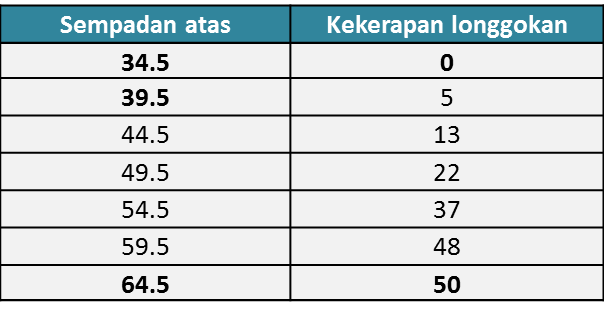

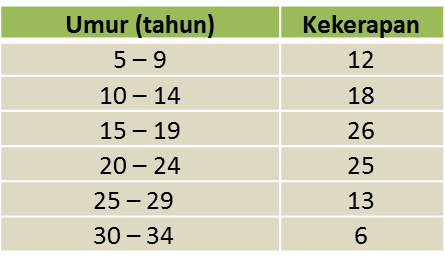
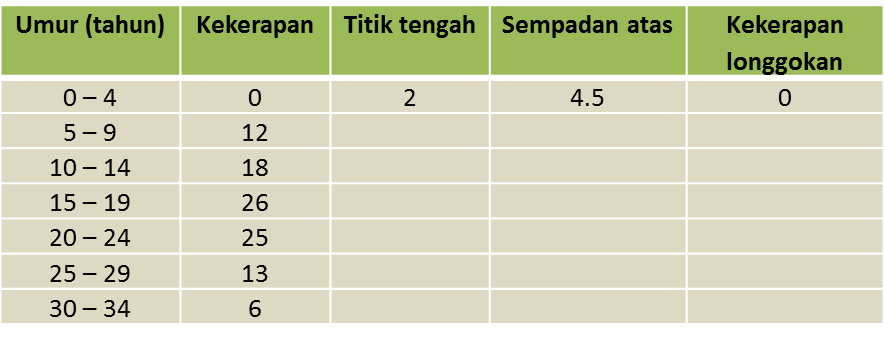
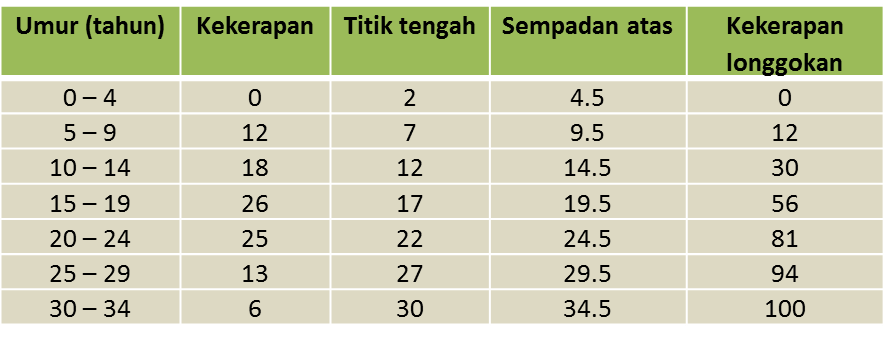
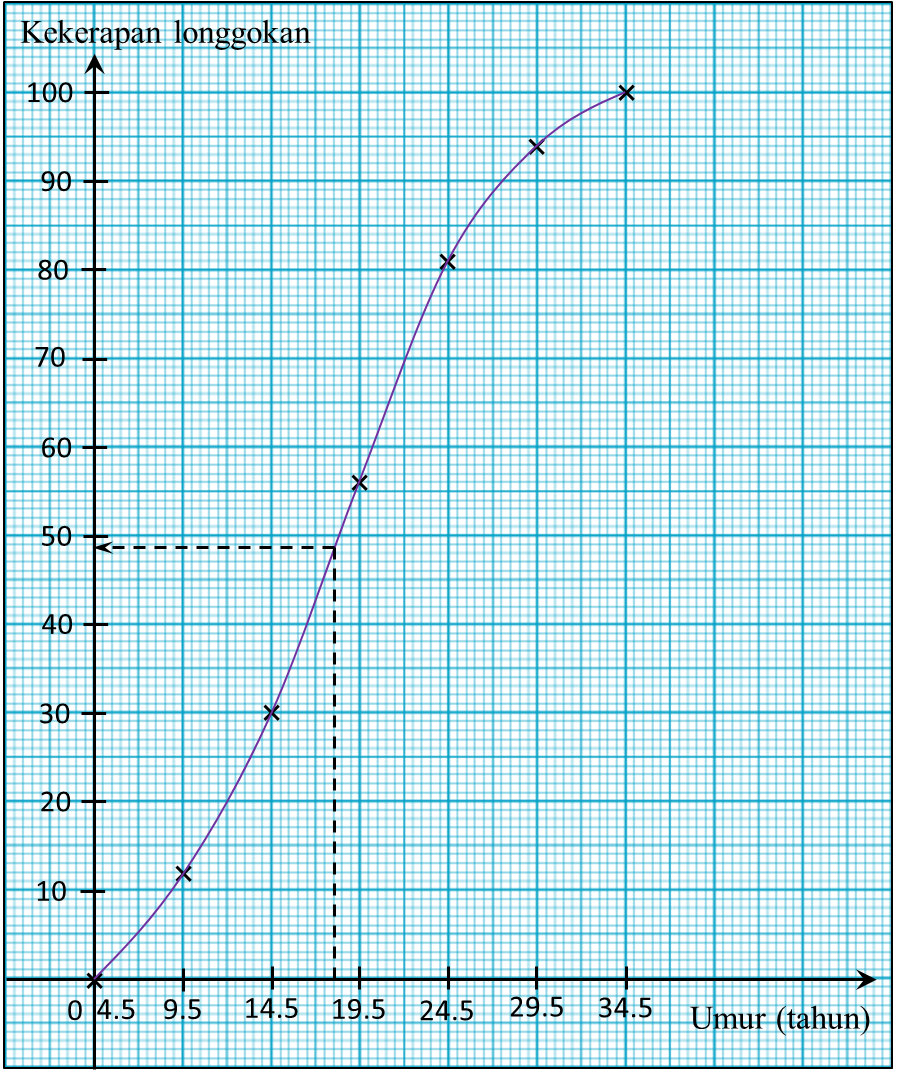
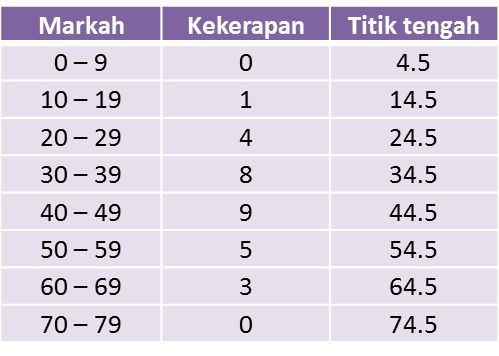
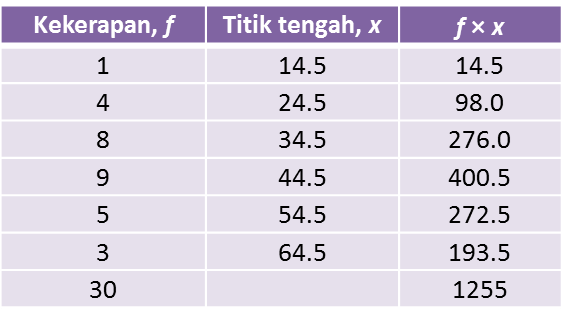
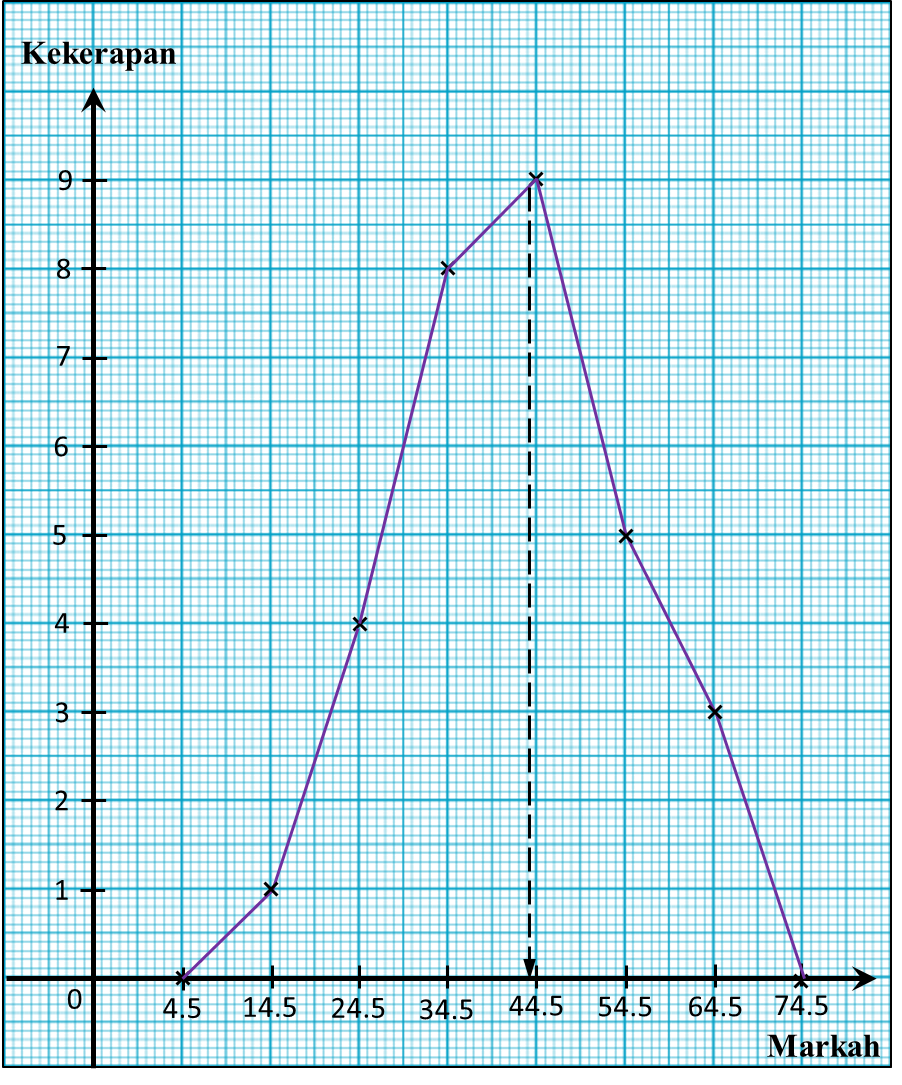
 Jadual 2
Jadual 2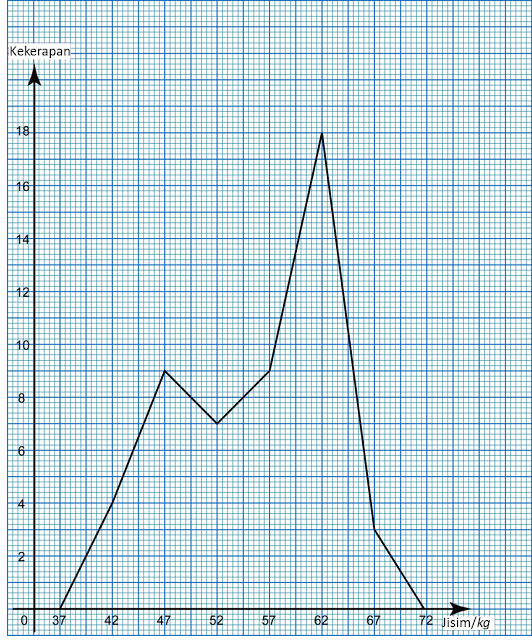
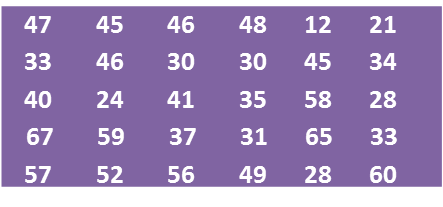
 Jadual 1
Jadual 1
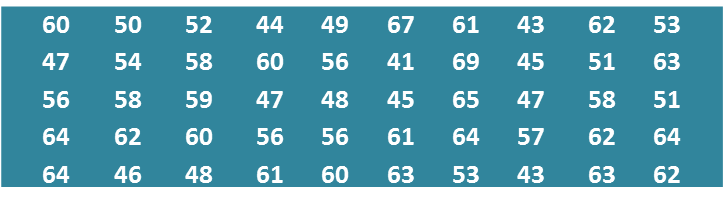
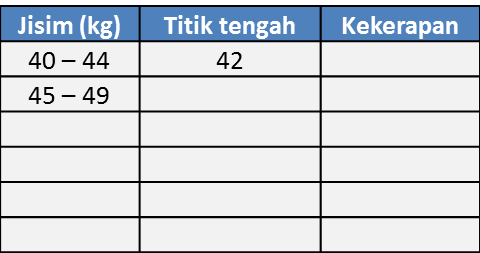
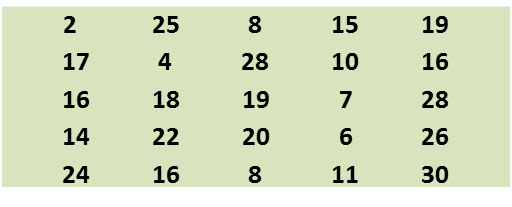
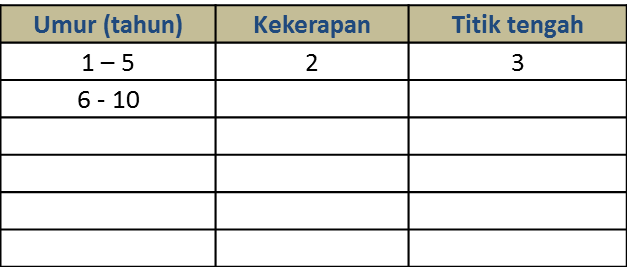
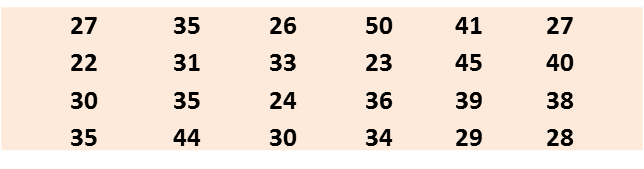 (a) Berdasarkan data di rajah di atas, lengkapkan Jadual di ruang jawapan.
(a) Berdasarkan data di rajah di atas, lengkapkan Jadual di ruang jawapan.