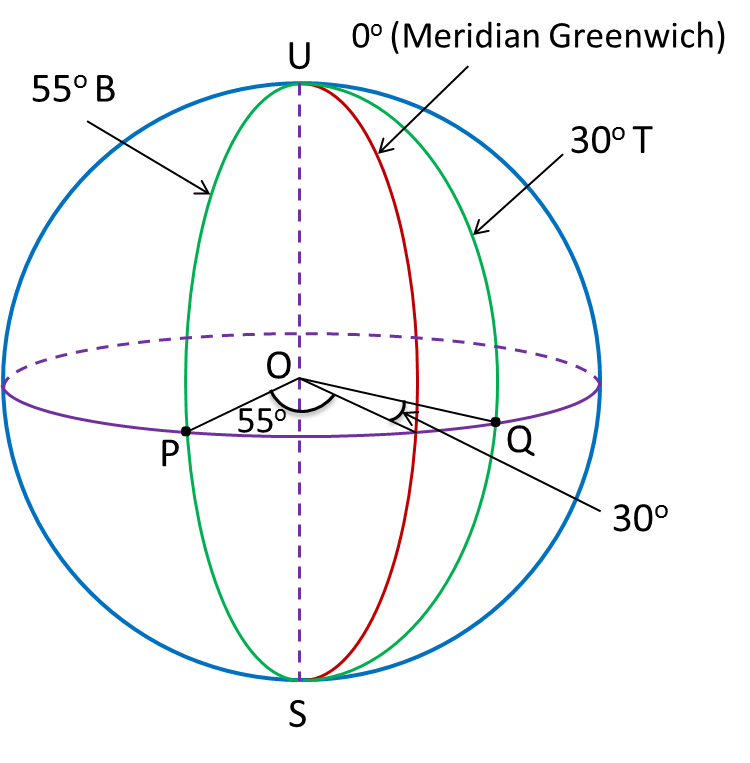
9.2 Latitud
1. Bulatan agong yang satahnya berserenjang dengan paksi bumi dikenali sebagai Khatulistiwa.
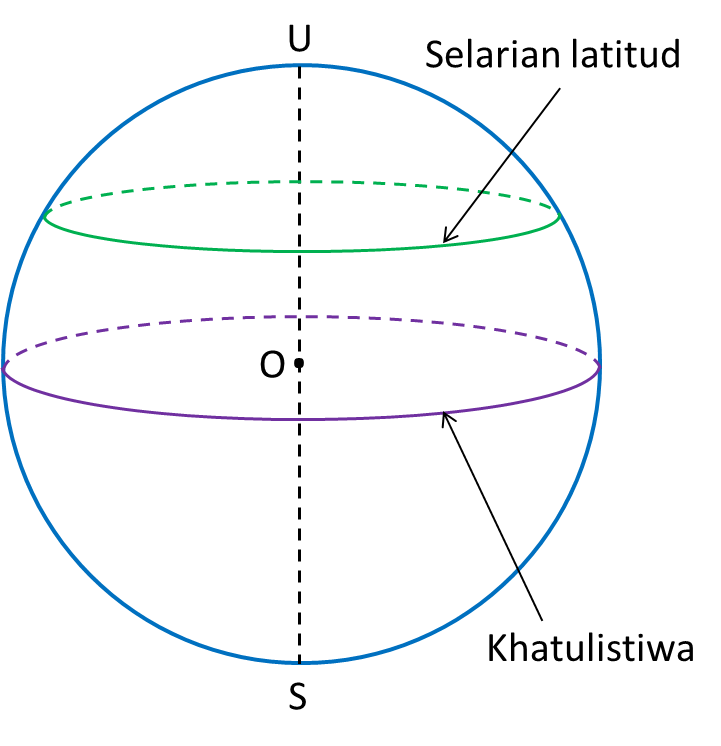

2. Bulatan yang satahnya berserenjang dengan paksi bumi dan selari dengan satah khatulistiwa dikenali sebagai selarian latitud.
3. Latitud ialah sudut pada pusat bumi yang dicangkum oleh lengkok suatu meridian bermula dari Khatulistiwa ke selarian latitud.
4. Latitud Khatulistiwa ialah 0o.
5. Semua titik pada selarian latitud yang sama mempunyai latitud yang sama.
Contoh:
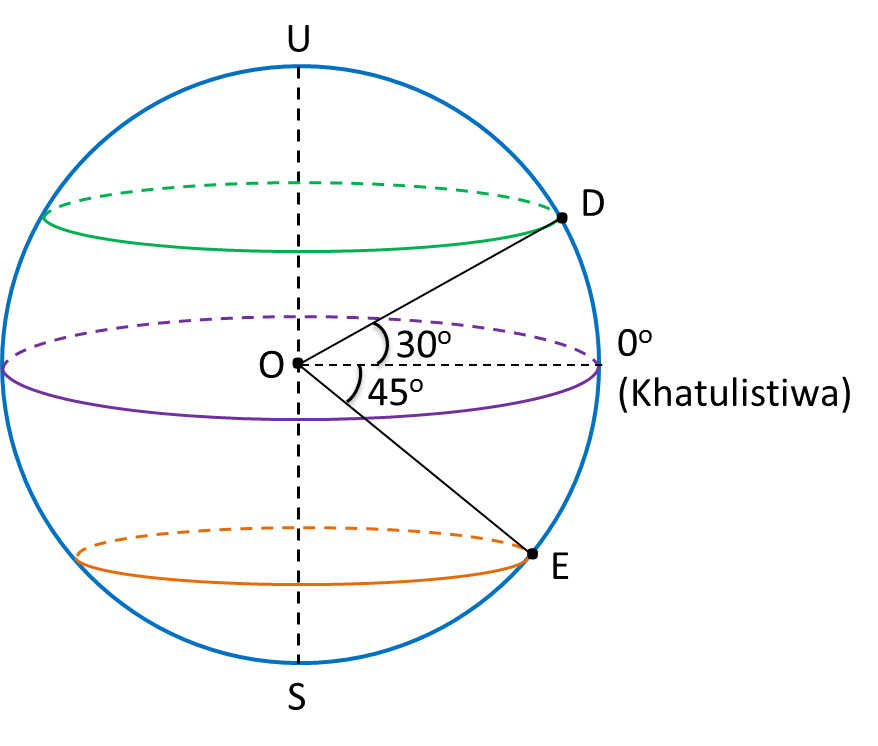 Latitud bagi D ialah 30o U.
Latitud bagi D ialah 30o U.Latitud bagi E ialah 45o S.
Beza di antara Dua Latitud
1. Jika kedua-dua selarian latitud berada ke utara atau ke selatan Khatulistiwa, menolakkan sudut-sudut latitud mereka untuk mencari beza antara dua latitud.
2. Jika satu selarian latitud berada ke utara Khatulistiwa dan satu selarian latitud yang lain berada ke selatan Khatulistiwa, menambahkan sudut-sudut latitud mereka untuk mencari beza antara dua latitud.