Bab 3 Set

Posted on April 28, 2016 by user

3.2c Set Pelengkap

1. Set pelengkap bagi set B dalam set semesta, ξ ialah satu set yang mengandungi semua unsur dalam set semesta yang bukan unsur B.

2. Set pelengkap bagi set B diwakilkan dengan menggunakan symbol B’.

Contoh:

Jika ξ = {17, 18, 19, 20, 21, 22, 23} dan

B = {17, 20, 21}

B’ = {18, 19, 22, 23}

3. Gambar rajah Venn di bawah menunjukkan hubungan antara B, B’ dan set semesta, ξ.

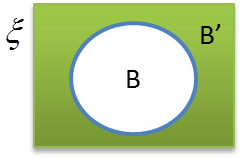
Set pelengkap bagi set B diwakilkan oleh rantau berlorek dalam set semesta, ξ, tetapi di luar set B.

Posted on April 28, 2016 by user

3.2b Set Semesta

1. Set semesta ialah set yang mengandungi semua unsur yang menjadi bahan perbincangan.

2. Set semesta diwakilkan dengan menggunakan symbol, ξ.

Contoh:

Diberi set semesta, ξ = {nombor bulat kurang daripada 9}, A = {nombor perdana} dan B = {gandaan bagi 4}.

(a) Senaraikan semua unsur bagi set A dan set B.

(b) Lukiskan gambar rajah Venn untuk mewakilkan hubungan antara set-set yang berikut.

(i) ξ dan A

(ii) ξ, A dan B

Penyelesaian:

(a) ξ = {0, 1, 2, 3, 4, 5, 6, 7, 8}

A= {2, 3, 5, 7}

B= {4, 8}

(b)(i)

(b)(ii)

Posted on April 28, 2016 by user

3.2 Subset, Set Semesta, dan Set Pelengkap

3.2a Subset

1. Set A ialah subset bagi set B jika semua unsur dalam set Aterdapat dalam set B.

2. Hubungan ‘set A ialah subset bagi set B’ ditulis sebagai

A \subset B .

Contoh:

A= {11, 12, 13} dan B = {10, 11, 12, 13, 14}

Semua unsur set Aterdapat dalam set B.

Oleh itu A \subset B .

A \subset B

boleh digambarkan dengan menggunakan gambar rajah Venn berikut:

4. Simbol

⊄

diguna untuk menandakan ‘bukan subset kepada’.

5. Set kosong adalah subsetbagi semua set.

Misalnya,

ϕ \subset A

6. Set itu sendiri adalah subset.

Misalnya,

B \subset B

7. Bilangan unsur, n bagi suatu subset adalah 2ⁿ.

Misalnya, jika A = {3, 7}

Maka n = 2, bilangan subset bagi set A = 2² = 4

Semua subset bagi set A ialah { }, {3}, {7} and {3, 7}.