6.2.2 Pythagoras’ Theorem, PT3 Focus Practice

Posted on August 8, 2017 by user

Question 6:
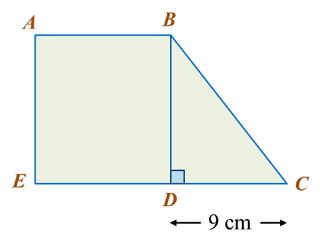
In diagram below, ABCH is a square and DEFG is a rectangle. HCDE is a straight line and HC = CD.

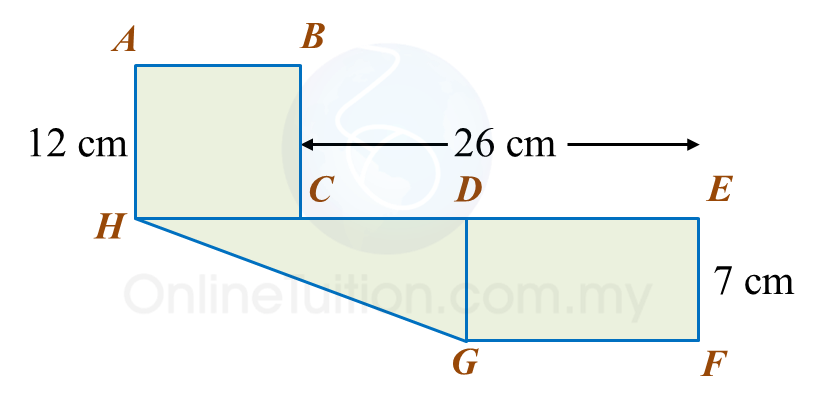
Find the perimeter, in cm, of the whole diagram.

Solution:

$\begin{array}{l} G H^{2} = D H^{2} + D G^{2} \\ = 24^{2} + 7^{2} \\ = 576 + 49 \\ = 625 \\ G H = 25 cm \\ Perimeter of the whole diagram \\ = 12 + 12 + 12 + 26 + 7 + 14 + 25 \\ = 108 cm \end{array}$

Question 7:
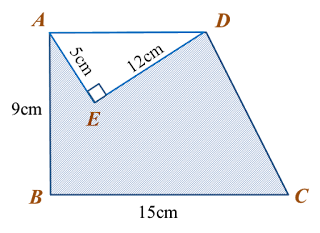
In the diagram, ABC and EFD are right-angled triangles.

Calculate the perimeter, in cm, of the shaded region.

Solution:

$\begin{array}{l} D E^{2} = 3^{2} + 4^{2} \\ = 9 + 16 \\ = 25 \\ D E = \sqrt{25} \\ = 5 cm \\ A C^{2} = 7^{2} + 24^{2} \\ = 49 + 576 \\ = 625 \\ A C = \sqrt{625} \\ = 25 cm \\ Perimeter of the shaded region \\ = 24 + 7 + (25 - 5) + 3 + 4 \\ = 58 cm \end{array}$

Question 8:
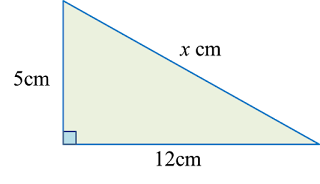
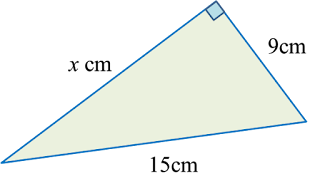
In the diagram, ABD and BCE are right-angled triangles. ABC and DBE are straight lines. The length of AB is twice the length of BC.

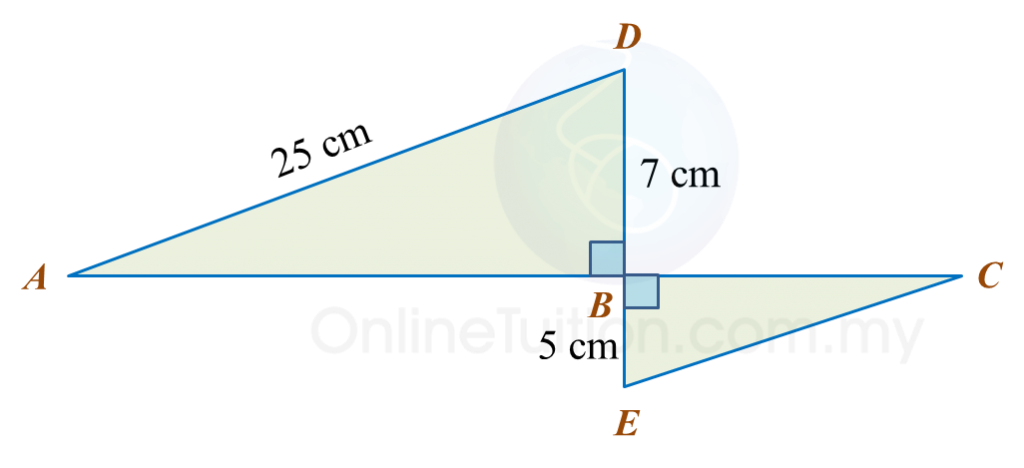
Calculate the length, in cm, of CE.

Solution:

$\begin{array}{l} A B^{2} = 25^{2} - 7^{2} \\ = 625 - 49 \\ = 576 \\ A B = \sqrt{576} \\ = 24 cm \\ B C = 24 cm \div 2 \\ = 12 cm \\ C E^{2} = 5^{2} + 12^{2} \\ = 25 + 144 \\ = 169 \\ C E = \sqrt{169} \\ = 13 cm \end{array}$

Question 9:
Diagram below shows two right-angled triangles, ABE and CBD. BED is a straight line.

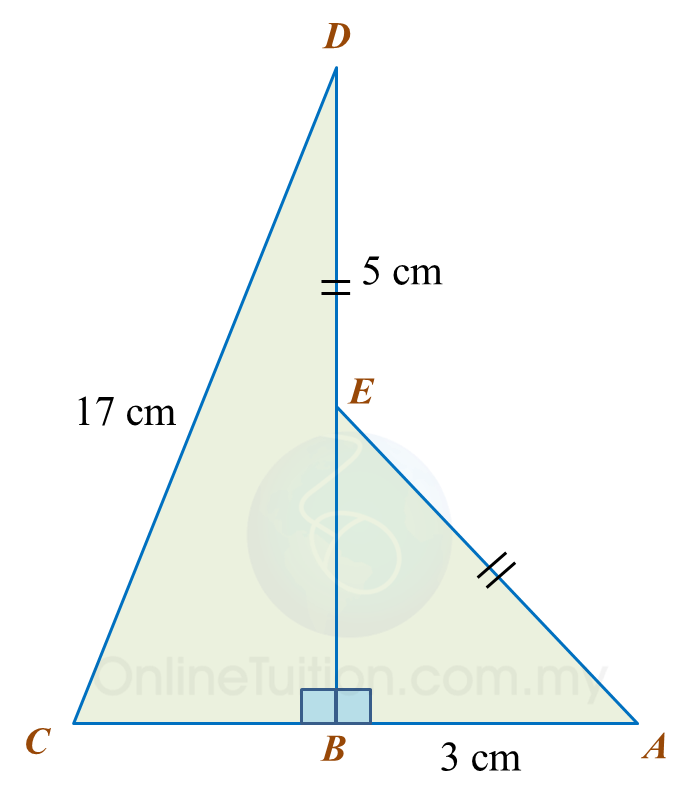Find the length, in cm, of BC. Round off the answer to two decimal places.

Solution:

$\begin{array}{l} 3^{2} + B E^{2} = 5^{2} \\ B E^{2} = 5^{2} - 3^{2} = 16 \\ B E = 4 cm \\ B C^{2} + {(5 + 4)}^{2} = 17^{2} \\ B C^{2} = 17^{2} - 9^{2} = 208 \\ B C = \sqrt{208} \\ B C = 14.42 cm \end{array}$

Question 10:
Diagram below shows two right-angled triangles, ABC and ADE. ACD is a straight line.

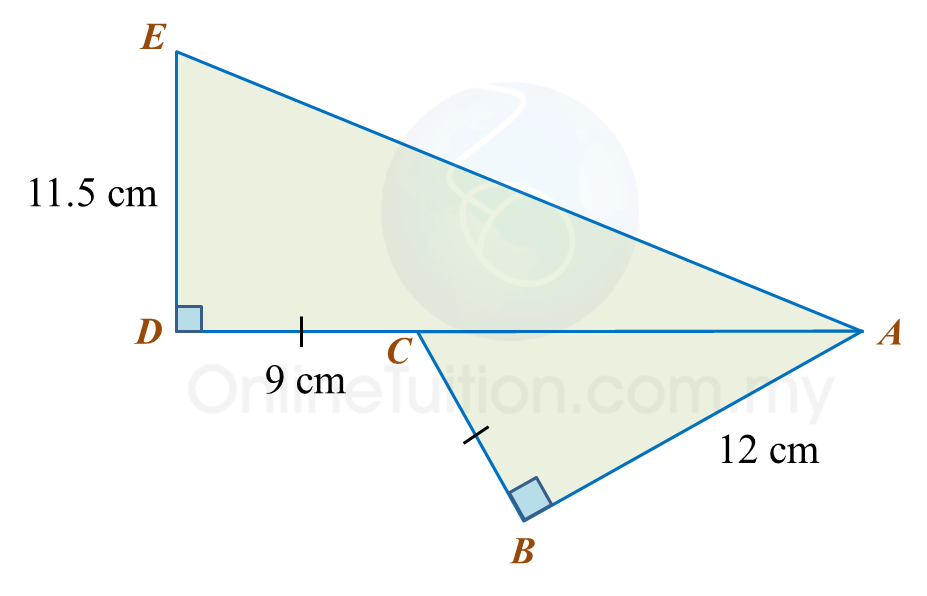Find the length, in cm, of AE. Round off the answer to one decimal places.

Solution:

$\begin{array}{l} A C^{2} = 12^{2} + 9^{2} \\ = 225 \\ A C = \sqrt{225} \\ = 15 cm \\ A E^{2} = {(15 + 9)}^{2} + {11.5}^{2} \\ = 576 + 132.25 \\ = 708.25 \\ A E = \sqrt{708.25} \\ = 26.6 cm \end{array}$

6.2.1 Pythagoras’ Theorem, PT3 Focus Practice

Posted on August 5, 2017 by user

6.2.1 Pythagoras’ Theorem, PT3 Focus Practice

Question 1:

In the diagram, ABC is a right-angled triangle and BCD is a straight line. Calculate the length of AD, correct to two decimal places.

Solution:

In ∆ ABC,

BC²= 5² – 4²

= 25 – 16

= 9

BC = √9

= 3 cm

In ∆ ABD,

BD = BC + CD

= 3 + 6

= 9

AD²= 4² + 9²

= 16 + 81

= 97

AD = √97

= 9.849

= 9.85 cm

Question 2:

In the diagram shows two right-angled triangles. Calculate the perimeter of the whole diagram.

Solution:

In ∆ ABC,

AC²= 6² + 8²

= 36 + 64

= 100

AC = √100

= 10 cm

AD = 5 cm

In ∆ EDC,

EC²= 12² + 5²

= 144 + 25

= 169

EC = √169

= 13 cm

Perimeter of the whole diagram

= AB + BC + CE + DE + AD

= 6 + 8 + 13 + 12 + 5

= 44 cm

Question 3:

Diagram below shows a triangle ACD and ABC is a straight line.

Calculate the length, in cm, of AD.

Solution:

In ∆ DBC,

BC²= 25² – 24²

= 625 – 576

= 49

BC = √49

= 7 cm

AB = 17 – 7 = 10 cm

In ∆ DAB,

AD²= 10² + 24²

= 100 + 576

= 676

AD = √676

= 26 cm

Question 4:

In diagram below ABDE is a square and EDC is a straight line.

The area of the square ABDE is 144 cm².

Calculate the length, in cm, of BC.

Solution:

BD = √144

= 12 cm

BC²= 12² + 9²

= 144 + 81

= 225

BC = √225

= 15 cm

Question 5:

In the diagram, ABCD is a trapezium and AED is a right-angled triangle.

Calculate the area, in cm², of the shaded region.

Solution:

AD²= 5² + 12²

= 25 + 144

= 169

AD = √169

= 13 cm

Area of trapezium ABDC

= ½ (13 + 15) × 9

= 126 cm²

Area of triangle AED

= ½ × 5 × 12

= 30 cm²

Area of the shaded region

= 126 – 30

= 96 cm²

6.1 Pythagoras’ Theorem

Posted on August 1, 2017 by user

6.1 Pythagoras’ Theorem

6.1.1 Pythagoras’ Theorem

1. In a right-angled triangle, the hypotenuse is the longest side of the triangle.

2. Pythagoras’ Theorem:

In a right-angled triangle, the square

of the hypotenuse is equal to the sum

of the squares of the other two sides.

Example 1:

Solution:

$\begin{array}{l} x^{2} = 5^{2} + 12^{2} \\ = 25 + 144 \\ x = \sqrt{169} \\ = 13 \end{array}$

Example 2:

Solution:

$\begin{array}{l} x^{2} = 15^{2} - 9^{2} \\ = 225 - 81 \\ x = \sqrt{144} \\ = 12 \end{array}$

3. Pythagorean triples are three whole numbers that form the sides of a right-angled triangle.

Example:

(a) 3, 4, 5
(b) 6, 8, 10

(e) 9, 12, 15

6.1.2 The Converse of the Pythagoras’ Theorem

In a triangle, if the sum of the squares of the two sides

is equal to the square of the longest side, then the angle

opposite the longest side is a right angle.