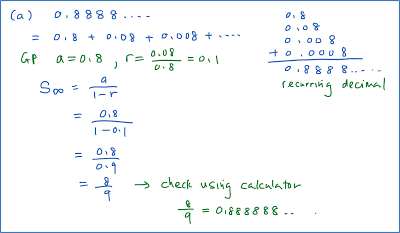
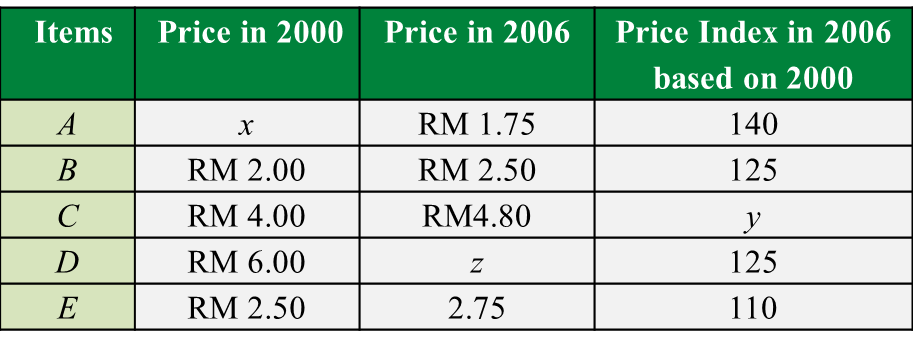
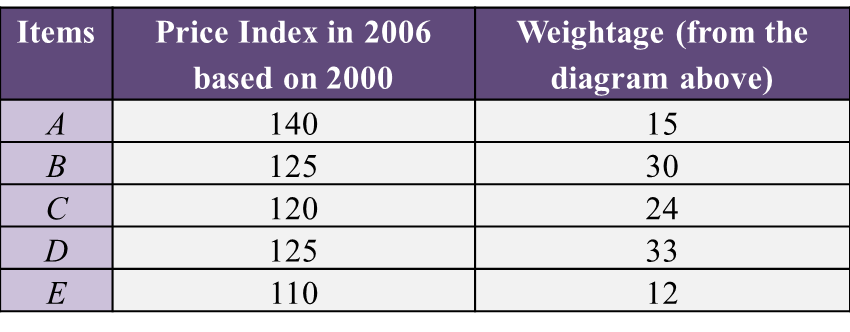
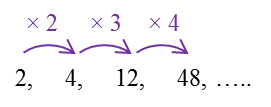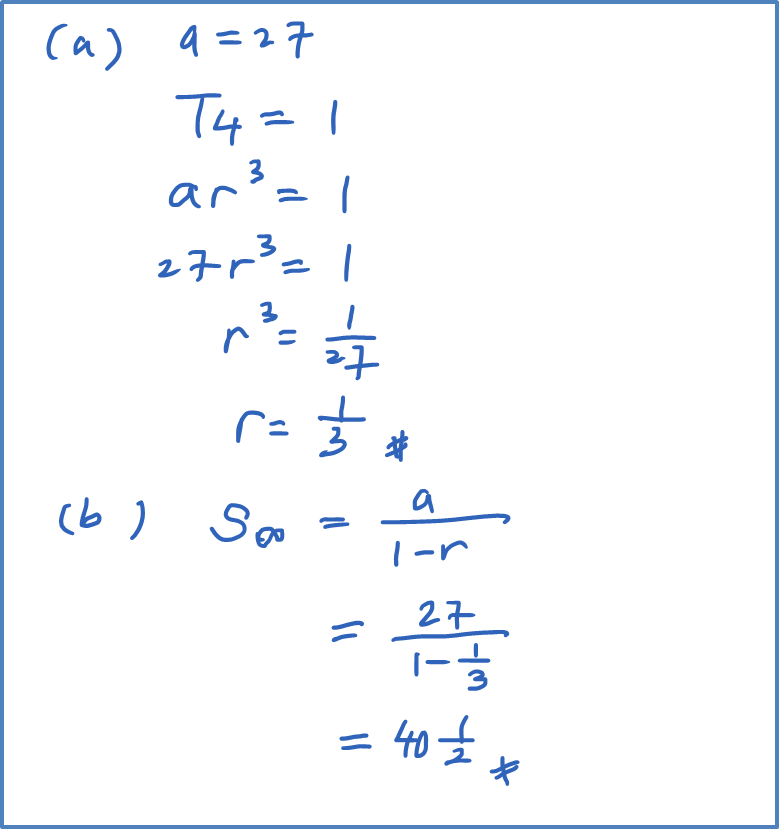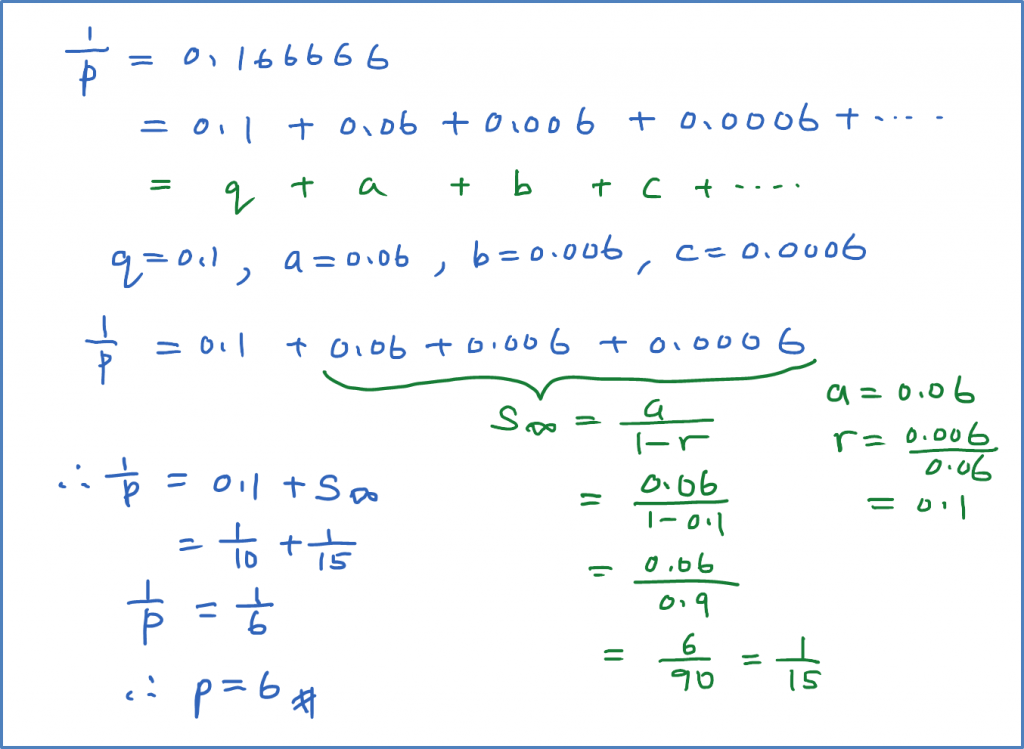Question 1:
Diagram below shows part of an arrangement of bricks of equal size.
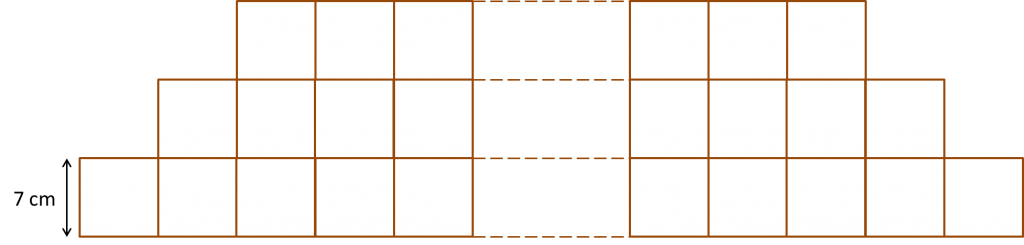
The number of bricks in the lowest row is 100. For each of the other rows, the number of bricks is 2 less than in the row below. The height of each brick is 7 cm.
Rahman builds a wall by arranging bricks in this way. The number of bricks in the highest row is 4. Calculate
(a) the height, in cm, of the wall.
(b) the total price of the bricks used if the price of one brick is 50 sen.
Solution:
100, 98, 96, …, 4 is an arithmetic progression
a = 100 and d = –2
(a)
Tn = 4
a + (n – 1) d = 4
100 + (n – 1)(–2) = 4
100 – 2n + 2 = 4
2n = 98
n = 49
Height of the wall = 49 × 7 = 343 cm
(b)
Total number of bricks used
= S49
=492(100+4)←Sn=n2(a+l)
= 2548
Total price = 2548 × RM0.50
= RM1,274
Diagram below shows part of an arrangement of bricks of equal size.

The number of bricks in the lowest row is 100. For each of the other rows, the number of bricks is 2 less than in the row below. The height of each brick is 7 cm.
Rahman builds a wall by arranging bricks in this way. The number of bricks in the highest row is 4. Calculate
(a) the height, in cm, of the wall.
(b) the total price of the bricks used if the price of one brick is 50 sen.
Solution:
100, 98, 96, …, 4 is an arithmetic progression
a = 100 and d = –2
(a)
Tn = 4
a + (n – 1) d = 4
100 + (n – 1)(–2) = 4
100 – 2n + 2 = 4
2n = 98
n = 49
Height of the wall = 49 × 7 = 343 cm
(b)
Total number of bricks used
= S49
=492(100+4)←Sn=n2(a+l)
= 2548
Total price = 2548 × RM0.50
= RM1,274