Home › Archive for SPM Add Maths › Page 8

SPM Add Maths

Long Questions (Question 9)

Posted on by

Question 9 (7 marks):
Mathematics Society of SMK Mulia organized a competition to design a logo for the society.


Diagram shows the circular logo designed by Adrian. The three blue coloured regions are congruent. It is given that the perimeter of the blue coloured region is 20π cm.
[Use π = 3.142]
Find
(a) the radius, in cm, of the logo to the nearest integer,
(b) the area, in cm2, of the yellow coloured region.

Solution:
(a)
6 arcs =20π 6rθ=20π 6r[ 60 o × π 180 o 3 ]=20π 2πr=20π r=10 cm

(b)

Area of yellow coloured region =3[ area of triangle OAB ]−6[ area of segment ] =3[ 1 2 absinC ]−6[ 1 2 r 2 ( θ−sinθ ) ] =3[ 1 2 ( 10 )( 10 )sin 120 o ]−6[ 1 2 ( 10 ) 2 ( θ−sinθ ) ] =3( 43.3013 )−6[ 50( 1.0473−sin1.0473 ) ]← change to rad mode θ= 60 o × 3.142 180 o =1.0473 =129.9039−6( 9.0612 ) =129.9039−54.3672 =75.54  cm 2


Long Questions (Question 10)

Posted on by

Question 10 (7 marks):
Solution by scale drawing is not accepted.
Diagram shows the locations of town M and town N drawn on a Cartesian plane.


PQ is a straight road such that the distance from town M and town N to any point on the road is always equal.
(a) Find the equation of PQ.

(b) Another straight road, ST with an equation y = 2x + 7 is to be built.
(i) A traffic light is to be installed at the crossroads of the two roads.
Find the coordinates of the traffic light.
(ii) Which of the two roads passes through town L  ( − 4 3 ,1 )?

Solution:
(a)
T( x,y ) is a point on PQ. TM=TN [ x− ( −4 ) 2 ]+ [ y−( −1 ) ] 2 = ( x−2 ) 2 + ( y−1 ) 2 ( x+4 ) 2 + ( y+1 ) 2 = ( x−2 ) 2 + ( y−1 ) 2 ( x+4 ) 2 + ( y+1 ) 2 = ( x−2 ) 2 + ( y−1 ) 2 x 2 +8x+16+ y 2 +2y+1 = x 2 −4x+4+ y 2 −2y+1 8x+2y+17+4x+2y−5=0 12x+4y+12=0 3x+y+3=0 Equation of PQ:3x+y+3=0


(b)(i)
y=2x+7   ............ ( 1 ) 3x+y+3=0 ............ ( 2 ) Substitute ( 1 ) into ( 2 ): 3x+2x+7+3=0 5x=−10 x=−2 When x=−2, From ( 1 ), y=2( −2 )+7=3 Coordinates of traffic light=( −2,3 ).


(b)(ii)
L( − 4 3 ,1 ):x=− 4 3 ,y=1 The equation of ST:y=2x+7 Left hand side: y=1 Right hand side: 2( − 4 3 )+7=4 1 3 Thus, the road y=2x+7 does not  pass through L. The equation of PQ:3x+y+3=0 Left hand side:  3x+y+3=3( − 4 3 )+1+3    =−4+4=0 Right hand side=0 Left hand side=Right hand side Thus, the road 3x+y+3=0 passes through L.


Long Questions (Question 9)

Posted on by

Question 9 (6 marks):
Solution by scale drawing is not accepted.
Diagram shows a triangle OCD.
Diagram

(a) Given the area of triangle OCD is 30 units2, find the value of h.

(b) Point Q (2, 4) lies on the straight line CD.
(i) Find CQ : QD.
(ii) Point P moves such that PD = 2 PQ.
  Find the equation of the locus P.

Solution:
(a)
Given Area of △ OCD = 30 1 2  | 0  h −6   0  2   8   0 0 |=30 | ( 0 )( 2 )+( h )( 8 )+( −6 )( 0 )−( 0 )( h )−( 2 )( −6 )−( 8 ) ( 0 )|=60 | 0+8h+0−0+12−0|=60 | 8h+ 12|=60 8h+12=60 8h=48 h=6 or  8h+12=−60 8h=−72 h=−9( ignore )


(b)(i)

[ 6( m )+( −6 )( n ) m+n ,  2( m )+( 8 )( n ) m+n ]=( 2, 4 ) 6m−6n m+n =2 6m−6n=2m+2n 4m=8n m n = 8 4 m n = 2 1 2m+8n m+n =4 2m+8n=4m+4n 2m=4n m n = 4 2 m n = 2 1 Thus, CQ=QD=2:1


(b)(ii)
PD=2PQ ( x−6 ) 2 + ( y−2 ) 2 =2 ( x−2 ) 2 + ( y−4 ) 2 ( x−6 ) 2 + ( y−2 ) 2 =4[ ( x−2 ) 2 + ( y−4 ) 2 ] x 2 −12x+36+ y 2 −4y+4=4[ x 2 −4x+4+ y 2 −8y+16 ] x 2 −12x+36+ y 2 −4y+4=4 x 2 −16x+16+4 y 2 −32y+64 The equation of locus P: 3 x 2 +3 y 2 −4x−28y+40=0


SPM Practice (Long Question)

Posted on by

Question 4:
The function f is denoted by f:x→ 1+x 1−x ,x≠1.  Find  f 2 , f 3 , f 4  and hence write down the functions  f 51  and  f 52 .

Solution:
f( x )= 1+x 1−x ,x≠1 f 2 ( x )=f[ f( x ) ]=f( 1+x 1−x )          = 1+( 1+x 1−x ) 1−( 1+x 1−x ) = 1−x+1+x 1−x 1−x−1−x 1−x          = 2 −2x =− 1 x f 3 ( x )=f[ f 2 ( x ) ]=f( − 1 x )          = 1+( − 1 x ) 1−( − 1 x ) = x−1 x x+1 x          = x−1 x+1 f 4 ( x )=f[ f 3 ( x ) ]=f( x−1 x+1 )           = 1+( x−1 x+1 ) 1−( x−1 x+1 ) = x+1+x−1 x+1 x+1−x+1 x+1           = 2x 2 =x f 5 ( x )=f[ f 4 ( x ) ]=f( x )= 1+x 1−x ( recurring ) ∴ f 51 ( x )= f 3 [ f 48 ( x ) ]= f 3 ( x )              = x−1 x+1 f 52 ( x )= f 4 [ f 48 ( x ) ]= f 4 ( x )=x


SPM Practice (Long Question)

Posted on by

Question 2:
The function f and g is defined by
f( x )=3x−2 g( x )= 3 x ,x≠0 Find (a)  f −1 ( 2 ), (b) gf( −3 ), (c) function h if hf( x )=3x+2, (d) function k if fk( x )=4x−7.

Solution:
(a)
Let  f −1 ( 2 )=x, thus  f( x )=2       3x−2=2            3x=4              x= 4 3 f −1 ( 2 )= 4 3

(b)
gf( −3 )=g[ 3( −3 )−2 ]            =g( −11 )            =− 3 11

(c)
h[ f( x ) ]=3x+2 h( 3x−2 )=3x+2 Let y=3x−2 thus     x= y+2 3      h( y )=3( y+2 3 )+2             =y+2+2             =y+4 ∴ h( x )=x+4

(d)
f[ k( x ) ]=4x−7 3k( x )−2=4x−7 3k( x )=4x−5 k( x )= 4x−5 3

SPM Practice (Long Question)

Posted on by

Question 6 (8 marks):
It is given that g : x → 2x – 3 and h : x → 1 – 3x.
(a) Find
(i) h (5)
(ii) the value of k if  g( k+2 )= 1 7 h( 5 ),
(iii) hg(x).

(b) Hence, sketch the graph of y = | hg(x) | for –1 ≤ x ≤ 3.
State the range of y.

Solution:
(a)(i)
h( x )=1−3x h( 5 )=1−3( 5 )    =−14

(a)(ii)
g( x )=2x−3 g( k+2 )= 1 7 h( 5 ) 2( k+2 )−3= 1 7 ( −14 ) 2k+4−3=−2 2k=−3 k=− 3 2

(a)(iii)
g( x )=2x−3, h( x )=1−3x hg( x )=h( 2x−3 )  =1−3( 2x−3 )  =1−6x+9  =10−6x

(b)
y = |hg(x)|,
y = |10 – 6x|
Range of y : 0 ≤ y ≤ 16





SPM Practice Question 6

Posted on by

Question 6 (7 marks):
Diagram shows part of a rectangular wall painted with green, G, blue, B and purple, P subsequently.
The height of the wall is 2 m. The side length of the first coloured rectangle is 5 cm and the side length of each subsequent coloured rectangle increases by 3 cm.


It is given that the total number of the coloured rectangles is 54.
(a) Find
(i) the side length, in cm, of the last coloured rectangle,
(ii) the total length, in cm, of the painted wall.
(b) Which coloured rectangle has an area of 28000 cm2?
  Hence, state the colour of that particular rectangle.

Solution:
(a)
5, 8, 11, …
a = 5, d = 3

(i)
T54 = 1 + (54 – 1)d
= 5 + 53(3)
=164 cm

(ii)
S n = n 2 ( a+l ) S 54 = 54 2 ( 5+164 )  =4563 cm


(b)
Area of the first rectangle
= 2 m × 5 cm
= 200 × 5
= 1000 cm

Area of the second rectangle
= 200 × (5 + 3)
= 1600 cm

Area of the third rectangle
= 200 × (5 + 3 + 3)
= 2200 cm

1000, 1600, 2200, …
a = 1000, d = 600
Tn = 28 000
a + (n – 1)d = 28 000
1000 + (n – 1)600 = 28 000
600(n – 1) = 27 000
n – 1 = 45
n = 46

The colour of that particular rectangle is green.


SPM Practice Question 5

Posted on by

Question 5 (6 marks):
The sum of the first n terms of an arithmetic progression, Sn is given by S n = 3n( n−33 ) 2 .  
Find
(a) the sum of the first 10 terms,
(b) the first term and the common difference,
(c) the value of q, given that qth term is the first positive term of the progression.

Solution:
(a)
S n = 3n( n−33 ) 2 S 10 = 3( 10 )( 10−33 ) 2 S 10 =−345

(b)
S n = 3n( n−33 ) 2 S 1 = 3( 1 )( 1−33 ) 2 S 1 =−48 T 1 = S 1 =−48 First term, a= T 1 =−48 T n = S n − S n−1 T 2 = S 2 − S 1 T 2 = 3( 2 )( 2−33 ) 2 −( −48 ) T 2 =−45 Common difference, d = T 2 − T 1 =−45−( −48 ) =3

(c)
First positive term,  T q >0 T q >0 a+( q−1 )d>0 −48+( q−1 )3>0 −48+3q−3>0 3q>51 q>17 Thus, q=18.


Long Questions (Question 10)

Posted on by

Question 10:
(a) It is found that 60% of the students from a certain class obtained grade A in English in O level trial examination.
If 10 students from the class are selected at random, find the probability that
(i) exactly 7 students obtained grade A.
(ii) not more than 7 students obtained grade A.

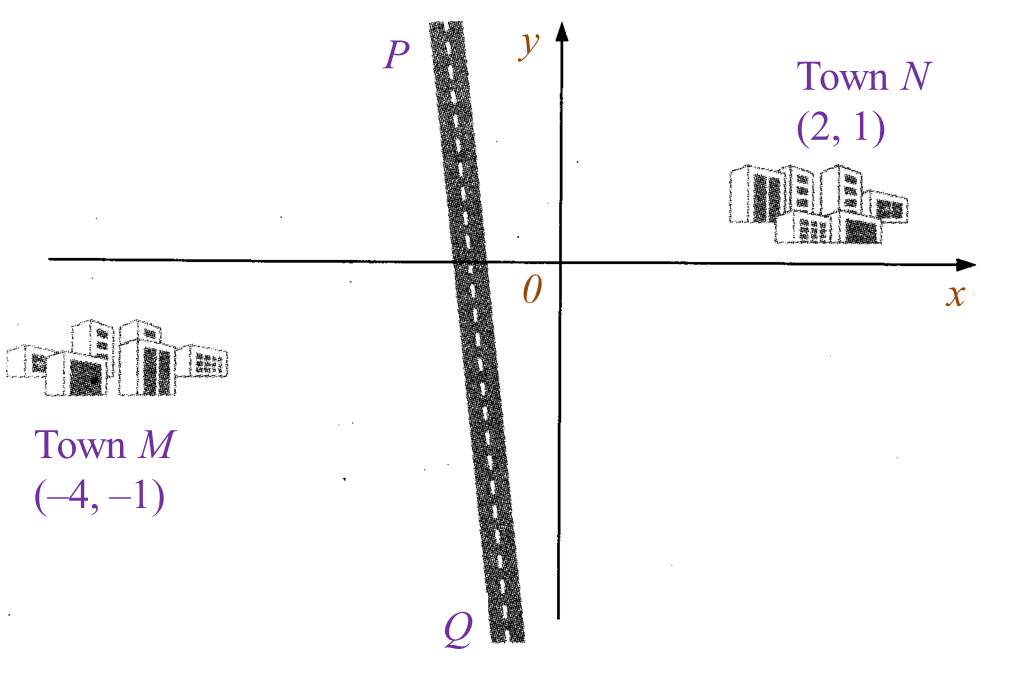
(b) Diagram below shows a standard normal distribution graph representing the volume of soy sauce in bottles produced by a factory.

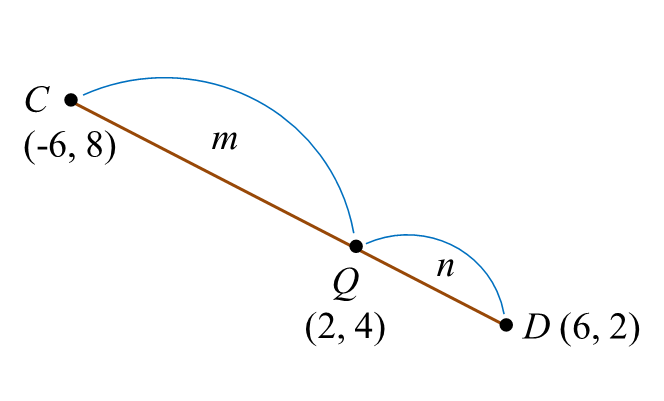
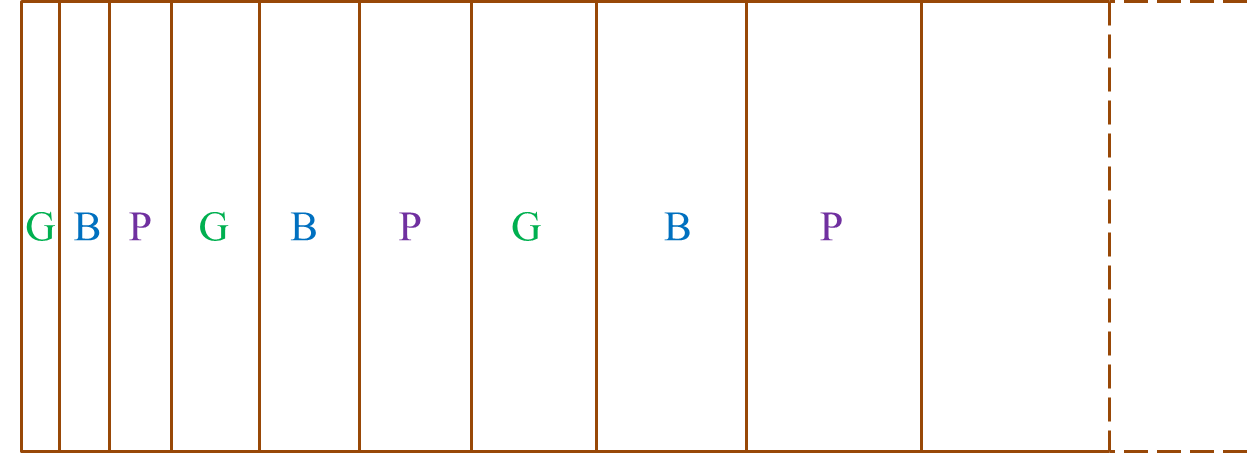
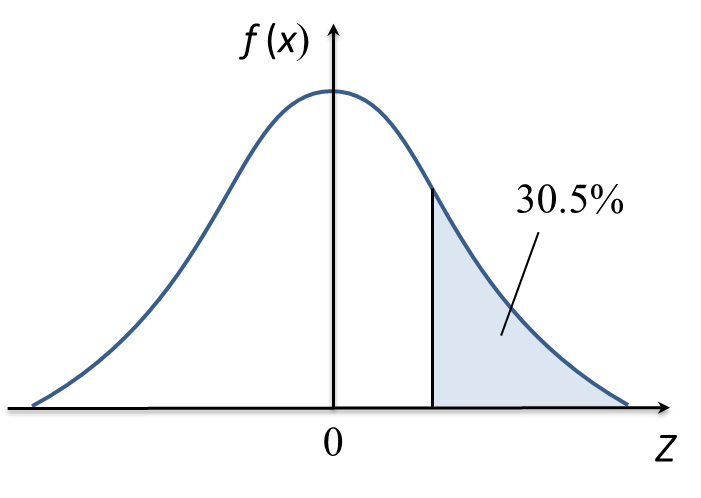It is given the mean is 950 cm3 and the variance is 256 cm6. If the percentage of the volume more than V is 30.5%, find
(i) the value of V,
(ii) the probability that the volume between 930 cm3 and 960 cm3.

Solution:
(a)(i) P(X=r)= c n r . p r . q n−r P(X=7)= C 10 7 ( 0.6 ) 7 ( 0.4 ) 3    =0.0860 ( ii ) P(X≤7) =1−P(X>7) =1−P( X=8 )−P( X=9 )−P( X=10 ) =1− C 10 8 ( 0.6 ) 8 ( 0.4 ) 2 − C 10 9 ( 0.6 ) 9 ( 0.4 ) 1 − C 10 10 ( 0.6 ) 10 ( 0.4 ) 0 =1−0.1209−0.0403−0.0060 =0.8328

(b)( i ) P( X>V )=30.5% P( Z> V−950 16 )=0.305 P( Z>0.51 )=0.305    V−950 16 =0.51 V=0.51( 16 )+950    =958.16  cm 3

( ii ) Probability =P( 930<X<960 ) =P( 930−950 16 <Z< 960−950 16 ) =P( −1.25<Z<0.625 ) =1−P( Z>1.25 )−P( Z>0.625 ) =1−0.1056−0.2660 =0.6284

Long Questions (Question 9)

Posted on by

Question 9:
(a) 30% of the pens in a box are blue. Charlie picks 4 pens at random. Find the probability that at least one pen picked is not blue.

(b) The mass of papayas harvested from an orchard farm follows a normal distribution with a mean of 2 kg and a standard deviation of h kg. It is given that 15.87% of the papayas have a mass more than 2.5 kg.
(i) Calculate the value of h.
(ii) Given the number of papayas harvested from the orchard farm is 1320, find the number of papayas that have the mass between 1.0 kg and 2.5 kg.

Solution:
 (a) P( X≥1 )=1−P( X=0 )               =1− C 4 4 ( 0.3 ) 4 ( 0.7 ) 0               =0.9919

(b) μ=2, σ=h ( i ) P( X>2.5 )=15.87% P( Z> 2.5−2 h )=0.1587 P( Z>1.0 )=0.1587        2.5−2 h =1.0                 h=0.5


( ii ) p=P( 1.0<x<2.5 )   =P( 1.0−2 0.5 <Z< 2.5−2 0.5 )   =P( −2<Z<1 )   =1−P( Z<−2 )−P( Z>1 )   =1−P( Z>2 )−P( Z>1 )   =1−0.0228−0.1587   =0.8185 Number of papayas=0.8185×1320   =1080