Question 10 (4 marks):
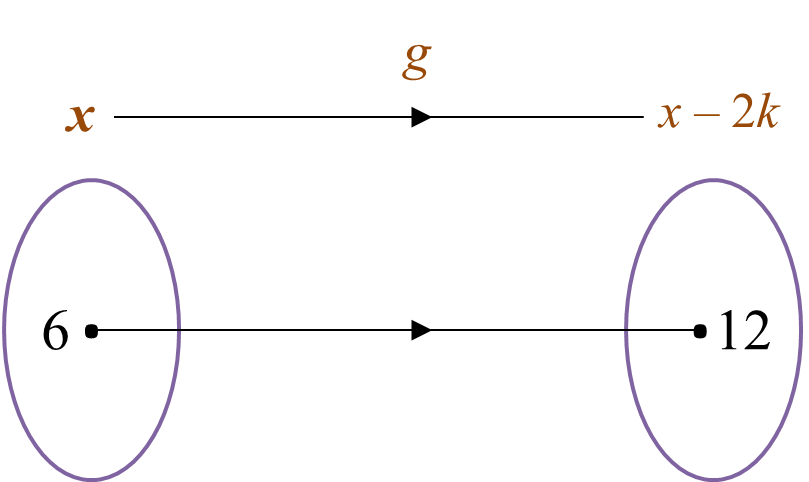
Given the function g : x → 2x – 8, find
Solution:
(a)
(b)
Given the function g : x → 2x – 8, find
Solution:
(a)
(b)
Question 11 (4 marks):
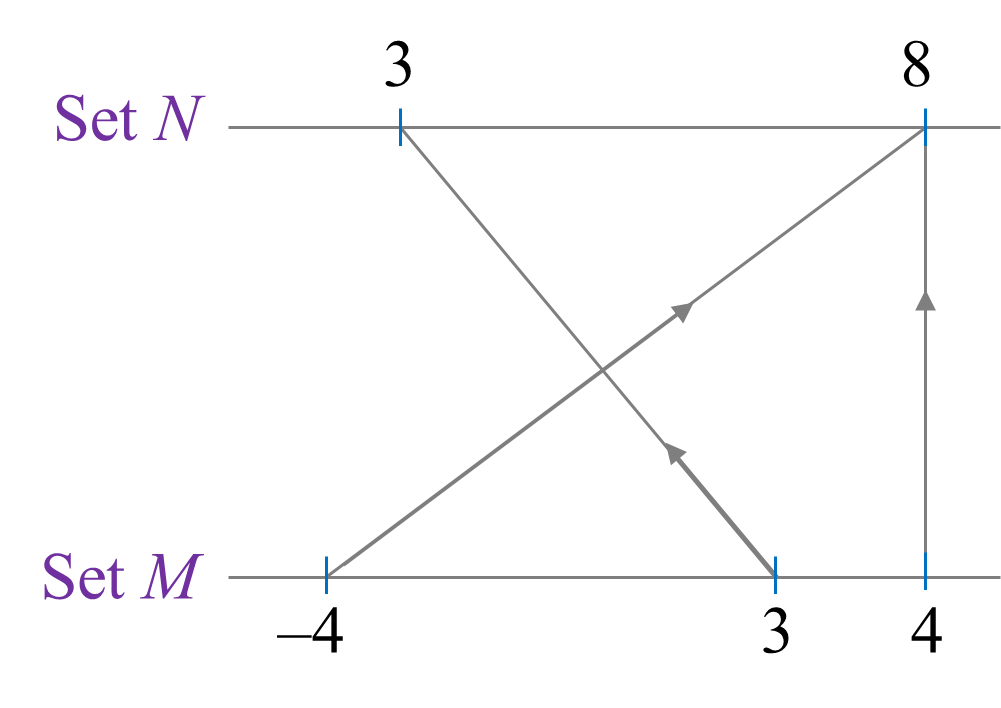
Diagram 9 shows the relation between set A, set B and set C.
 Diagram 9
Diagram 9
It is given that set A maps to set B by the function and maps to set C by fg : x → x2 + 2x + 4.
(a) Write the function which maps set A to set B by using the function notation.
(b) Find the function which maps set B to set C.
Solution:
 (a)
(a)
(b)
Diagram 9 shows the relation between set A, set B and set C.
 Diagram 9
Diagram 9It is given that set A maps to set B by the function and maps to set C by fg : x → x2 + 2x + 4.
(a) Write the function which maps set A to set B by using the function notation.
(b) Find the function which maps set B to set C.
Solution:
 (a)
(a)(b)


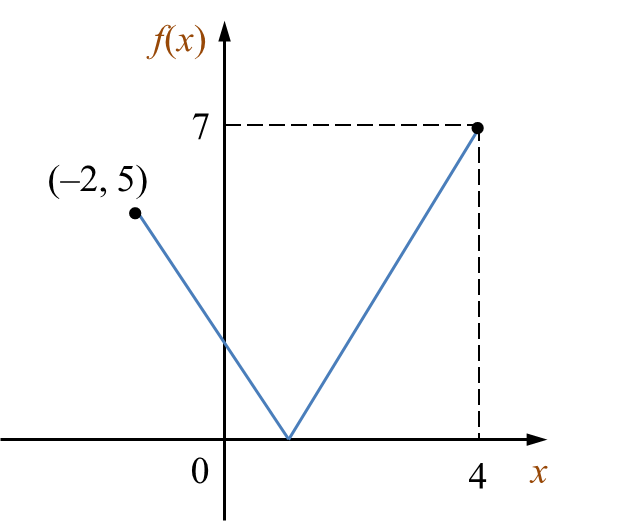 Diagram
Diagram 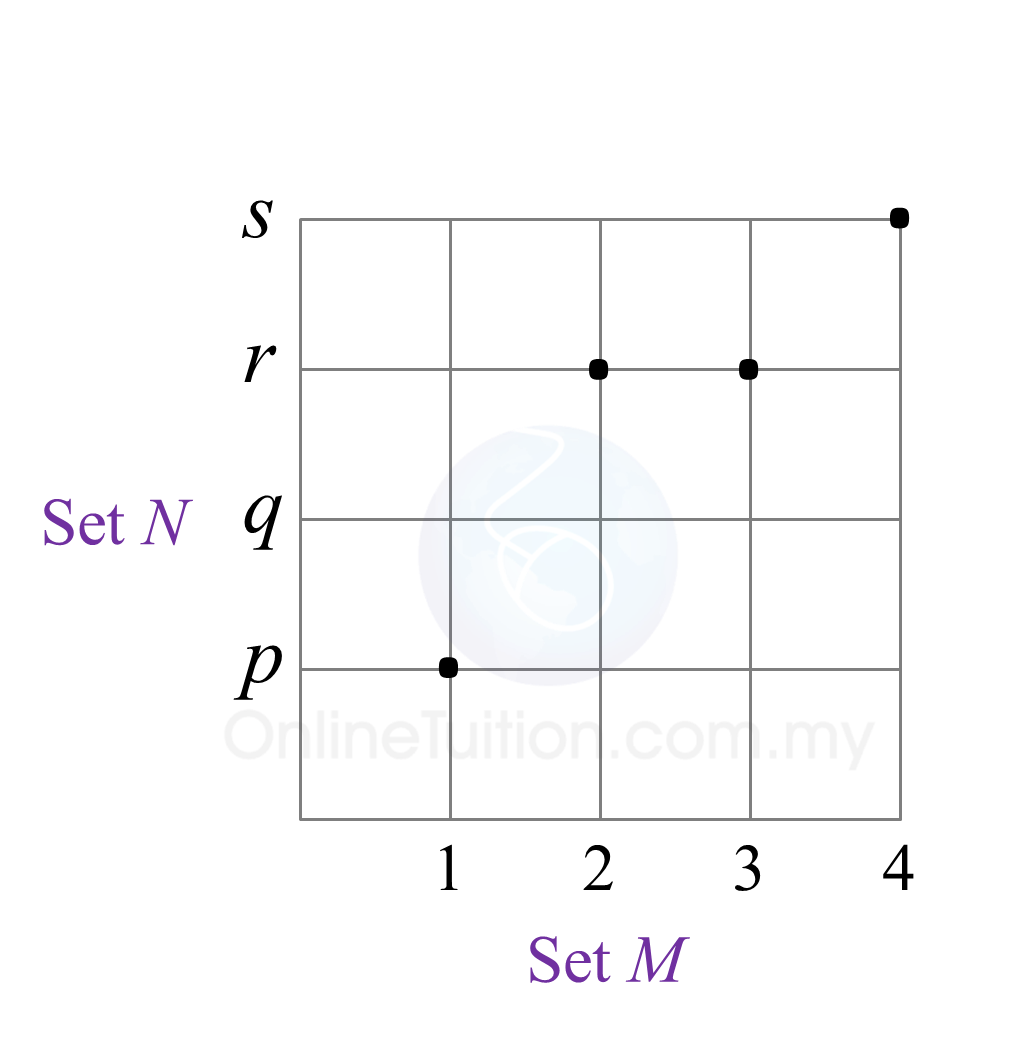 State
State