4.2.6 SPM Praktis, Persamaan Serentak

Posted on May 14, 2020 by Myhometuition

Soalan 10 (5 markah):
Selesaikan persamaan serentak berikut:
x – 3y = 1,
x²+ 3xy + 9y²= 7

Penyelesaian:

$\begin{array}{l} x - 3 y = 1................... (1) \\ x^{2} + 3 x y + 9 y^{2} = 7................... (2) \\ Daripada (1) : x = 3 y + 1................... (3) \\ Gantikan (3) ke dalam (2) : \\ {(3 y + 1)}^{2} + 3 (3 y + 1) y + 9 y^{2} = 7 \\ 9 y^{2} + 6 y + 1 + 9 y^{2} + 3 y + 9 y^{2} - 7 = 0 \\ 27 y^{2} + 9 y - 6 = 0 \\ 9 y^{2} + 3 y - 2 = 0 \\ (3 y - 1) (3 y + 2) = 0 \\ y = \frac{1}{3} atau - \frac{2}{3} \\ Gantikan y ke dalam (3) : \\ Apabila y = \frac{1}{3} \\ x = 3 (\frac{1}{3}) + 1 = 2 \\ Apabila y = - \frac{2}{3} \\ x = 3 (- \frac{2}{3}) + 1 = - 1 \\ Maka, penyelesaian ialah x = 2, y = \frac{1}{3} atau x = - 1, y = - \frac{2}{3} . \end{array}$

4.2.5 SPM Praktis, Persamaan Serentak

Posted on May 14, 2020 by Myhometuition

Soalan 9 (7 markah):
Rajah menunjukkan plan bagi sebuah taman berbentuk segi empat tepat ABCD. Taman itu terdiri daripada sebuah kolam berbentuk semi bulatan ATD dan kawasan berumput ABCDT.

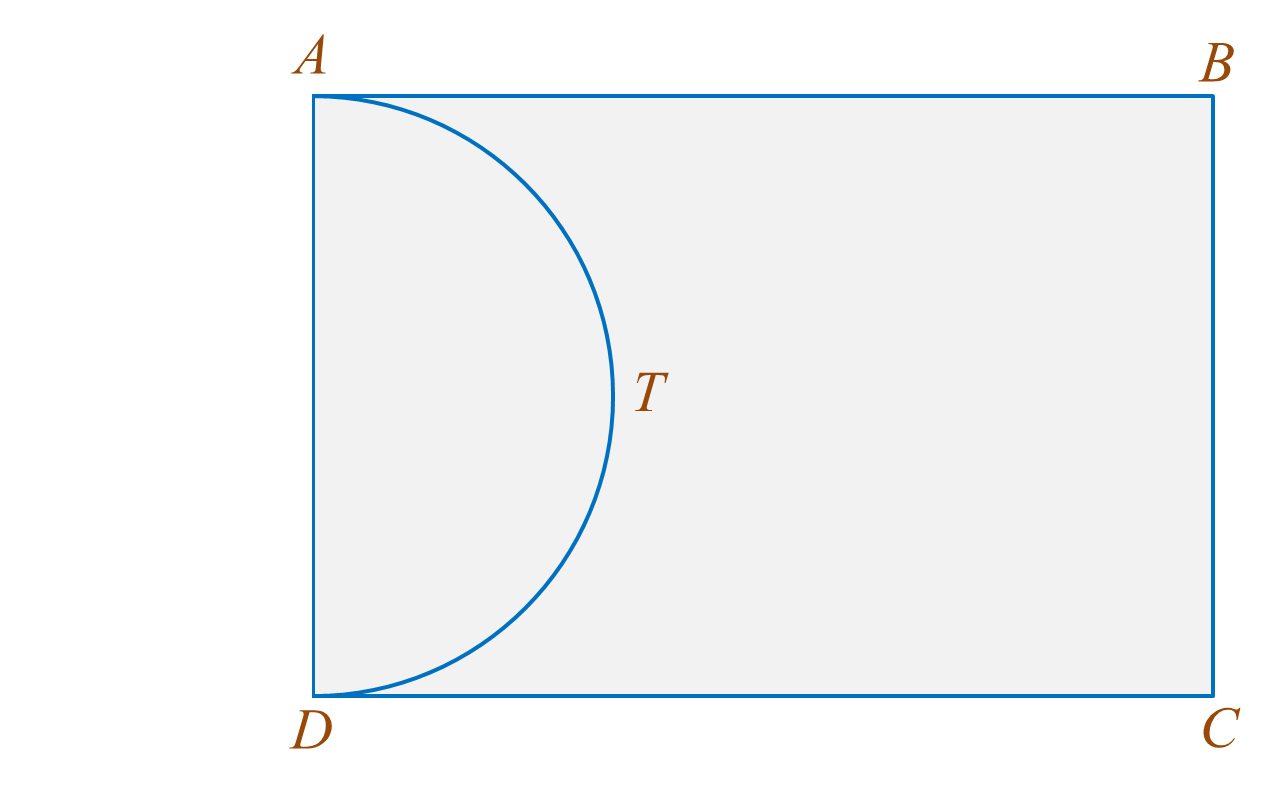Diberi bahawa DC = 6y meter dan BC = 7x meter, x ≠ y. Luas taman berbentuk segi empat tepat ABCD ialah 168 meter² dan perimeter kawasan berumput ialah 60 meter. Kolam dengan kedalaman seragam mengandungi 15.4 meter³ air.
Dengan menggunakan

$π = \frac{22}{7}$ , cari kedalaman, dalam meter, air dalam kolam itu.

Penyelesaian:

$\begin{array}{l} Luas A B C D = 168 \\ (6 y) (7 x) = 168 \\ 42 x y = 168 \\ x y = 4................... (1) \\ Perimeter kawasan berumput = 60 \\ 6 y + 6 y + 7 x + (\frac{1}{2} \times 2 \times \frac{22^{11}}{7} \times \frac{7 x}{2}) = 60 \\ 12 y + 18 x = 60 \\ 2 y + 3 x = 10................... (2) \\ Daripada (1) : x y = 4 \\ x = \frac{4}{y} ................... (3) \\ Gantikan (3) ke dalam (2): \\ 2 y + 3 (\frac{4}{y}) = 10 \\ 2 y^{2} + 12 = 10 y \\ y^{2} - 5 y + 6 = 0 \\ (y - 2) (y - 3) = 0 \\ y - 2 = 0 \\ y = 2 \\ Atau \\ y - 3 = 0 \\ y = 3 \\ Gantikan nilai-nilai bagi y ke dalam (3): \\ Apabila y = 2 \\ x = \frac{4}{2} = 2 (abaikan, x \neq y) \\ Apabila y = 3 \\ x = \frac{4}{3} \\ Diberi isi padu air = 15.4 \\ \frac{1}{2} (\frac{22}{7}) {(\frac{7 x}{2})}^{2} d = 15.4 \\ \frac{1}{2} (\frac{22}{7}) {[\frac{7 (\frac{4}{3})}{2}]}^{2} d = 15.4 \\ \frac{11}{7} {(\frac{14}{3})}^{2} d = 15.4 \\ \frac{308}{9} d = 15.4 \\ d = 0.45 m \\ Oleh itu, kedalaman air dalam kolam ialah 0 .45 m . \end{array}$

4.2.4 SPM Praktis, Persamaan Serentak

Posted on May 13, 2020 by Myhometuition

Soalan 7:
Diberi perimeter sebuah segi empat tepat ialah 24 cm dan luasnya ialah 35 cm² . Cari panjang dan lebar segi empat tepat itu.

Penyelesaian:
Anggap panjang = x cm dan lebar = y cm.
Diberi perimeter = 24 cm
Maka, 2x + 2y = 24
x + y = 12 ------ (1)

Diberi luas = 112 cm²
Maka, xy = 35 ------ (1)

Dari persamaan (1): y = 12 – x ------ (3)
Ganti (3) ke dalam (2):
x (12 – x) = 35
12x – x² = 35
x² – 12x + 35 = 0
(x – 5)(x – 7) = 0
x = 5, 7

Ganti x = 5 ke dalam (3):
y = 12 – 5 = 7

Ganti x = 7 ke dalam (3):
y = 12 – 7 = 5

Maka,
panjang = 5 cm dan lebar = 7 cm
atau
panjang = 7 cm dan lebar = 5 cm.

Soalan 8:

Dalam rajah di atas, PQRS ialah sekeping kertas berbentuk segi empat tepat dengan luas 112 cm² . STR berbentuk semibulatan digunting daripada kertas itu. Perimeter kertas yang tinggal ialah 52 cm. Dengan menggunakan π = 22/7, hitung nilai-nilai integer x dan y.

Penyelesaian:
Diberi luas PQRS = 112 cm²
Maka, (14x)(2y) = 112
28xy = 112
xy = 4 ------ (1)

Diberi perimeter kertas yang tinggal PSTRQ = 52 cm
PS + QR + PQ + Panjang lengkok STR = 52
2y + 2y + 14x + ½ (2πr) = 52
4y + 14x + (22/7) (7x) = 52
4y + 14x + 22x = 52
4y + 36x = 52
y + 9x = 13 ------ (2)

Dari persamaan (2): y = 13 – 9x ------ (3)

Ganti (3) ke dalam (1):
x (13 – 9x) = 4
13x – 9x² = 4
9x² – 13x + 4 = 0
(x – 1)(9x – 4) = 0
x = 1 atau 4/9 (bukan integer)

Dari (3):
Nilai integer x = 1,
Nilai integer y yang sepadan
= 13 – 9(1)
= 4.

Bab 4 Persamaan Serentak

Posted on October 10, 2016 by user

4.2 SPM Praktis, Persamaan Serentak, (Soalan panjang)

Soalan 5:

Selesaikan persamaan serentak.

5y – 6x= 2

$\frac{4 y}{x} - \frac{3 x}{y} = 4.$

Penyelesaian:

5y – 6x= 2 ----- (1)

$\begin{array}{l} \frac{4 y}{x} - \frac{3 x}{y} = 4 ------- (2) \\ Daripada (1), \\ y = \frac{2 + 6 x}{5} ------- (3) \end{array}$

Gantikan (3) dalam (2),

$\begin{array}{l} \frac{4 (\frac{2 + 6 x}{5})}{x} - \frac{3 x}{(\frac{2 + 6 x}{5})} = 4 \\ \frac{8 + 24 x}{5 x} - \frac{15 x}{2 + 6 x} = 4 \\ \frac{(8 + 24 x) (2 + 6 x) - (15 x) (5 x)}{5 x (2 + 6 x)} = 4 \end{array}$

16 + 48x + 48x + 144x² – 75x² = 20x (2 + 6x)

69x² + 96x + 16 = 40x + 120x²

51x² – 56x – 16 = 0

(3x – 4)(17x + 4) = 0

3x – 4 = 0 atau 17x + 4 = 0

$x = \frac{4}{3} atau x = - \frac{4}{17}$

$\begin{array}{l} Gantikan x = \frac{4}{3} dalam persamaan (3), \\ y = \frac{2 + 6 (\frac{4}{3})}{5} = 2 \end{array}$

$\begin{array}{l} Gantikan x = - \frac{4}{17} dalam persamaan (3), \\ y = \frac{2 + 6 (- \frac{4}{17})}{5} = \frac{2}{17} \end{array}$

$Maka penyelesaian ialah (\frac{4}{3}, 2) dan (- \frac{4}{17}, \frac{2}{17}) .$

Soalan 6:
Selesaikan persamaan serentak.

$\begin{array}{l} x + 2 y = 1 \\ 2 x^{2} + y^{2} + x y = 5 \end{array}$
Beri jawapan anda betul kepada tiga tempat perpuluhan.

Penyelesaian:

$\begin{array}{l} x + 2 y = 1.......... (1) \\ 2 x^{2} + y^{2} + x y = 5.......... (2) \\ x = 1 - 2 y .......... (3) \\ Gantikan (3) ke dalam (2), \\ 2 {(1 - 2 y)}^{2} + y^{2} + (1 - 2 y) y = 5 \\ 2 (1 - 4 y + 4 y^{2}) + y^{2} + y - 2 y^{2} = 5 \\ 2 - 8 y + 8 y^{2} - y^{2} + y - 5 = 0 \\ 7 y^{2} - 7 y - 3 = 0 \\ a = 7, b = - 7, c = - 3 \\ x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ y = \frac{- (- 7) \pm \sqrt{{(- 7)}^{2} - 4 (7) (- 3)}}{2 (7)} \\ y = \frac{7 \pm \sqrt{133}}{14} \\ y = 1.324 atau - 0.324 \\ Dari x = 1 - 2 y \\ Apabila y = 1.324, \\ x = 1 - 2 (1.324) = 1.648 \\ Apabila y = - 0.324, \\ x = 1 - 2 (- 0.324) = 1.648 \\ ∴ Penyelesaian ialah (1.648, 1.324) dan (1.648, - 0.324) . \end{array}$

Bab 4 Persamaan Serentak

Posted on May 10, 2016 by user

Soalan 3:

Selesaikan persamaan serentak.

3y – 2x= – 4

y² + 4x² = 2

Penyelesaian:

3y – 2x= – 4 -----(1)

y² + 4x²= 2 -----(2)

$\begin{array}{l} Dari (1), \\ y = \frac{2 x - 4}{3} ------- (3) \\ Gantikan (3) ke dalam (2), \\ {(\frac{2 x - 4}{3})}^{2} + 4 x^{2} = 2 \\ (\frac{4 x^{2} - 16 x + 16}{9}) + 4 x^{2} = 2 \\ 4 x^{2} - 16 x + 16 + 36 x^{2} = 18 (\times 9) \\ 40 x^{2} - 16 x - 2 = 0 \\ 20 x^{2} - 8 x - 1 = 0 \\ (10 x + 1) (2 x - 1) = 0 \\ x = - \frac{1}{10} atau x = \frac{1}{2} \\ Gantikan nilai-nilai x ke dalam (3), \\ Apabila x = - \frac{1}{10}, \\ y = \frac{2 (- \frac{1}{10}) - 4}{3} = - 1 \frac{2}{5} \\ Apabila x = \frac{1}{2}, \\ y = \frac{2 (\frac{1}{2}) - 4}{3} = - \frac{3}{3} = 1 \\ Penyelesaian ialah x = - \frac{1}{10}, y = - 1 \frac{2}{5} dan x = \frac{1}{2}, y = 1. \end{array}$

Soalan 4:

Selesaikan persamaan serentak x – 3y = –1 dan y + yx– 2x = 0.

Beri jawapan anda betul kepada tiga tempat perpuluhan.

Penyelesaian:

x – 3y = –1 -----(1)

y + yx – 2x = 0 -----(2)

Dari (1),

x = 3y – 1 -----(3)

Gantikan (3) ke dalam (2),

y + y (3y – 1) – 2(3y – 1) = 0

y + 3y² – y – 6y+ 2 = 0

3y² – 6y + 2 = 0

$\begin{array}{l} a = 3, b = - 6, c = 2 \\ y = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ y = \frac{- (- 6) \pm \sqrt{{(- 6)}^{2} - 4 (3) (2)}}{2 (3)} \\ y = \frac{6 \pm \sqrt{12}}{6} \\ y = 1.577 atau 0 .423 \end{array}$

Gantikan nilai-nilai y ke dalam (3).

Apabila y = 1.577,

x = 3 (1.577) – 1 = 3.731 (tiga tempat perpuluhan)

Apabila y = 0.423,

x = 3 (0.423) – 1 = 0.269 (tiga tempat perpuluhan)

Penyelesaian ialah x = 3.731, y = 1.577 dan x = 0.269, y = 0.423.

Bab 4 Persamaan Serentak

Posted on May 10, 2016 by user

4.2 SPM Praktis, Persamaan Serentak, (Soalan panjang)

Soalan 1:

Selesaikan persamaan serentak.

$\begin{array}{l} y + 2 x = 2 \\ \frac{2}{x} + \frac{1}{y} = 5 \end{array}$

Penyelesaian:

$\begin{array}{l} y + 2 x = 2 - - - - (1) \\ \frac{2}{x} + \frac{1}{y} = 5 - - - - (2) \\ y = 2 - 2 x - - - - (3) \\ Gantikan (3) ke dalam (2), \\ \frac{2}{x} + \frac{1}{2 - 2 x} = 5 \\ \frac{2 (2 - 2 x) + x}{x (2 - 2 x)} = 5 \\ 4 - 4 x = 5 x (2 - 2 x) \\ 4 - 4 x = 10 x - 10 x^{2} \\ 10 x^{2} - 14 x + 4 = 0 \\ 5 x^{2} - 7 x + 2 = 0 \\ (5 x - 2) (x - 1) = 0 \\ 5 x - 2 = 0 or x - 1 = 0 \\ x = \frac{2}{5} or x = 1 \\ Gantikan nilai-nilai x ke dalam (3), \\ Apabila x = \frac{2}{5}, \\ y = 2 - 2 (\frac{2}{5}) = 1 \frac{1}{5} \\ Apabila x = 1 \\ y = 2 - 2 (1) = 0 \\ Penyelesaian ialah x = \frac{2}{5}, y = 1 \frac{1}{5} dan x = 1, y = 0 \end{array}$

Soalan 2:

Selesaikan persamaan serentak.

x – 3y + 5 = 3y + 5y²– 6 – x = 0

Penyelesaian:

x – 3y + 5 = 0

x = 3y – 5 -----(1)

3y + 5y² – 6 – x = 0 -----(2)

Gantikan (1) ke dalam (2),

3y + 5y² – 6 – (3y – 5) = 0

3y + 5y² – 6 – 3y + 5 = 0

5y² – 1 = 0

5y² = 1

y = 0.447

Gantikan nilai-nilai yke dalam (1),

Apabila y = 0.447

x = 3 (0.447) – 5

x = –3.659

Apabila y = – 0.447

x = 3 (–0.447) – 5

x = –6.341

Penyelesaian ialah x = –3.659, y = 0.447 dan x = –6.341, y = – 0.447.

Bab 4 Persamaan Serentak

Posted on May 10, 2016 by user

4.1 Persamaan Serentak (contoh 1 & 2)

Contoh 1:

Selesaikan persamaan serentak,

$x + \frac{1}{4} y = 1 dan y^{2} - 8 = 4 x .$

Penyelesaian:

$\begin{array}{l} x + \frac{1}{4} y = 1 \to (1) \\ y^{2} - 8 = 4 x \to (2) \\ x = 1 - \frac{1}{4} y \to (3) \end{array}$

$\begin{array}{l} Gantikan (3) ke dalam (2), \\ y^{2} - 8 = 4 (1 - \frac{1}{4} y) \\ y^{2} - 8 = 4 - \frac{4}{4} y \\ y^{2} + y - 12 = 0 \\ (y + 4) (y - 3) = 0 \\ y = - 4 atau y = 3 \end{array}$

$\begin{array}{l} Gantikan nilai-nilai y ke dalam (3), \\ apabila y = - 4, \\ x = 1 - \frac{1}{4} (- 4) = 2 \\ apabila y = 3, \\ x = 1 - \frac{1}{4} (3) = \frac{1}{4} \end{array}$

Penyelesaian ialah x = 2, y = –4 dan x = ¼, y = 3.

Contoh 2:

Selesaikan persamaan serentak 2x + y = 1 dan 2x² + y² + xy = 5.

Beri jawapan anda betul kepada tiga tempat perpuluhan.

Penyelesaian:

2x + y = 1-----(1)

2x²+ y² + xy = 5-----(2)

Dari (1),

y= 1 – 2x-----(3)

Gantikan (3) ke dalam (2).

2x²+ (1 – 2x)² + x(1 – 2x) = 5

2x²+ (1 – 2x)(1 – 2x) + x – 2x² = 5

1 – 2x – 2x + 4x²+ x – 5 = 0

4x²– 3 x – 4 = 0

$\begin{array}{l} Dari x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ a = 4, b = - 3, c = - 4 \\ x = \frac{- (- 3) \pm \sqrt{{(- 3)}^{2} - 4 (4) (- 4)}}{2 (4)} \\ x = \frac{3 \pm \sqrt{73}}{8} \\ x = - 0.693 or 1.443 \end{array}$

Gantikan nilai-nilai x ke dalam (3).

Apabila x= –0.693,

y = 1 – 2 (–0.693) = 2.386 (tiga tempat perpuluhan)

Apabila x= 1.443,

y = 1 – 2 (1.443) = –1.886 (tiga tempat perpuluhan)

Penyelesaian ialah x = –0.693, y = 2.386 dan x = 1.443, y = –1.886.

Bab 4 Persamaan Serentak

Posted on May 10, 2016 by user

4.1 Persamaan Serentak

(A) Langkah-langkah penyelesaian persamaan serentak:

Susun persamaan linear supaya satu daripada anu-anu itu menjadi perkara rumus bagi persamaan itu.
Gantikan persamaan linear ke dalam persamaan tak linear.
Permudahkan dan ungkapkan persamaan yang diperoleh daripada langkah kedua dalam bentuk am persamaan kuadratik ax² + bx + c = 0

Selesaikan persamaan kuadratik.
Cari nilai anu yang kedua dengan menggantikan nilai anu pertama yang diperolehi ke dalam persamaan linear.

Contoh:

Selesaikan persamaan serentak.

y + x = 9

xy = 20

Penyelesaian:

Langkah1: Susun persamaan linear supaya satu daripada anu itu menjadi perkara rumus bagi persamaan itu

y + x = 9 ---- (1)

xy = 20 ---- (2)

y = 9 – x ----(3)

Langkah 2: Gantikan persamaan linear (persamaan (3) dari langkah (1) ke dalam persamaan tak linear.

xy = 20

x (9 – x) = 20

9x – x² = 20

Langkah 3: Permudahkan dan ungkapkan persamaan yang diperoleh daripada langkah 2 dalam bentuk am persamaan kuadratik ax² + bx + c = 0

9x – x² = 20

x² – 9x+ 20 = 0

Langkah 4:Selesaikan persamaan kuadratik.

x² – 9x+ 20 = 0

(x – 4) (x – 5) = 0

x = 4 or x = 5

Langkah 5:Cari nilai anu yang kedua dengan menggantikan nilai anu pertama yang diperolehi ke dalam persamaan linear.

Apabila x = 4,

y = 9 – x

y = 9 – 4 = 5

Apabila x = 5,

y = 9 – x

y = 9 – 5 = 4

Penyelesaian ialah x = 4, y = 5 dan x = 5, y = 4.