Question 12 (5 marks):
Diagram 7 shows a distance-time graph for the journey of a car from Kuala Lumpur to Ipoh.

(a) State the duration of time, in minutes, the driver stopped and rest at Tapah.
(b) Calculate the speed, in kmh-1, of the car from Kuala Lumpur to Tapah.
(c) Calculate the average speed, in kmh-1, of the car for whole journey.
Solution:
(a)
1400 – 1345 = 15 minutes
The driver stopped and rest at Tapah for 15 minutes.
(b)
Speed=DistanceTimeSpeed=152 km134 h←1345−1200=1 h 45 minsSpeed=86.86 kmh−1Speed of the car from Kuala Lumpurto Tapah=86.86 kmh−1
(c)
Average speed=Total distanceTime taken =205 km313 h←1520−1200=3 h 20 minsAverage speed=61.5 kmh−1Average speed of the car for thewhole journey=61.5 kmh−1
Diagram 7 shows a distance-time graph for the journey of a car from Kuala Lumpur to Ipoh.

(a) State the duration of time, in minutes, the driver stopped and rest at Tapah.
(b) Calculate the speed, in kmh-1, of the car from Kuala Lumpur to Tapah.
(c) Calculate the average speed, in kmh-1, of the car for whole journey.
Solution:
(a)
1400 – 1345 = 15 minutes
The driver stopped and rest at Tapah for 15 minutes.
(b)
Speed=DistanceTimeSpeed=152 km134 h←1345−1200=1 h 45 minsSpeed=86.86 kmh−1Speed of the car from Kuala Lumpurto Tapah=86.86 kmh−1
(c)
Average speed=Total distanceTime taken =205 km313 h←1520−1200=3 h 20 minsAverage speed=61.5 kmh−1Average speed of the car for thewhole journey=61.5 kmh−1
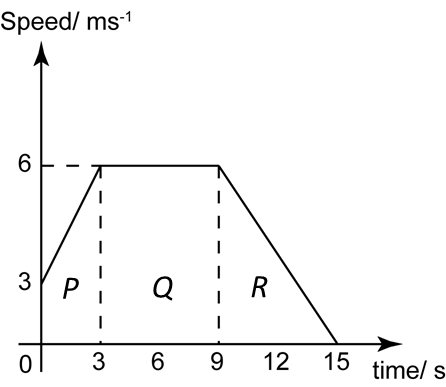
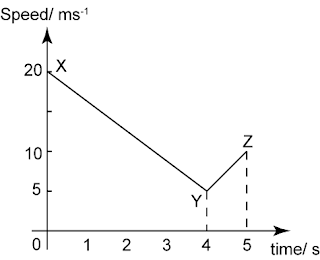
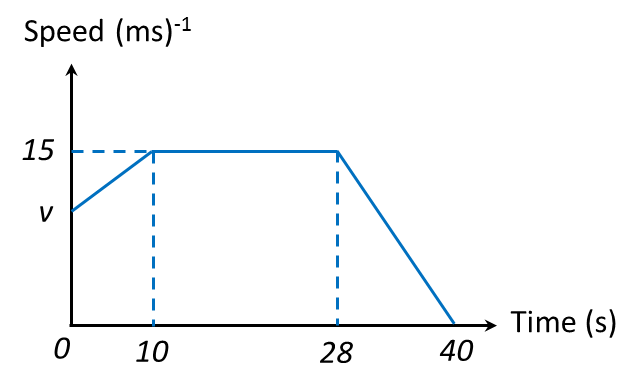
 Diagram 6
Diagram 6
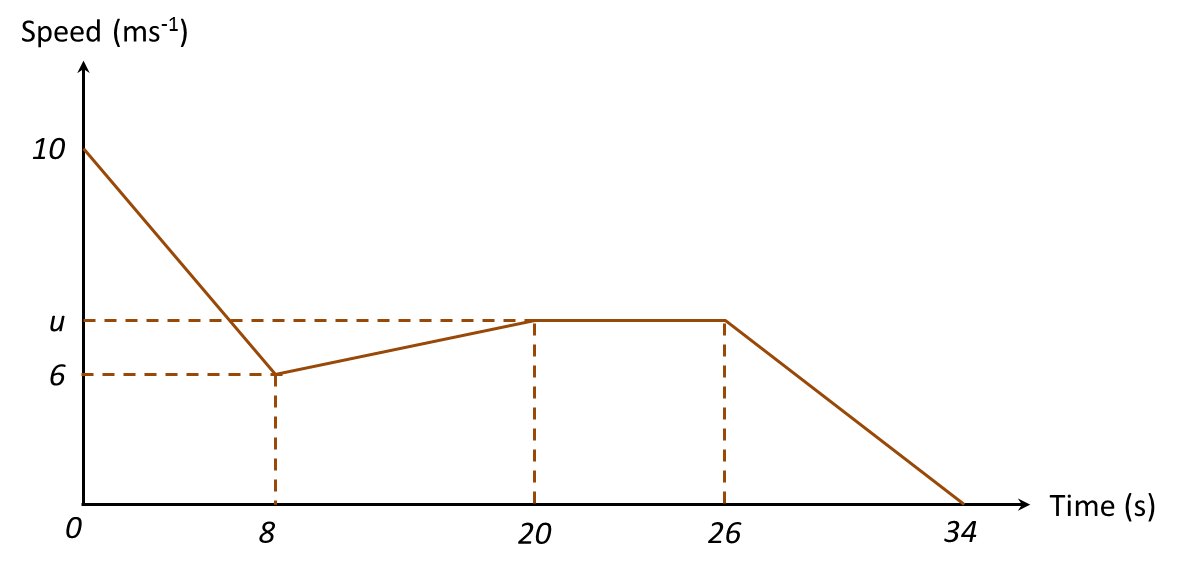
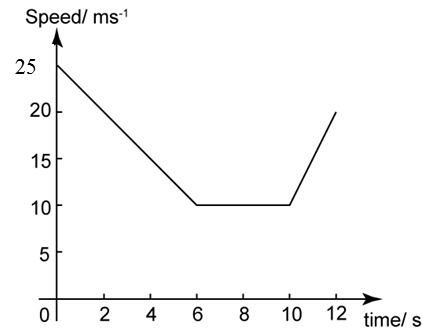
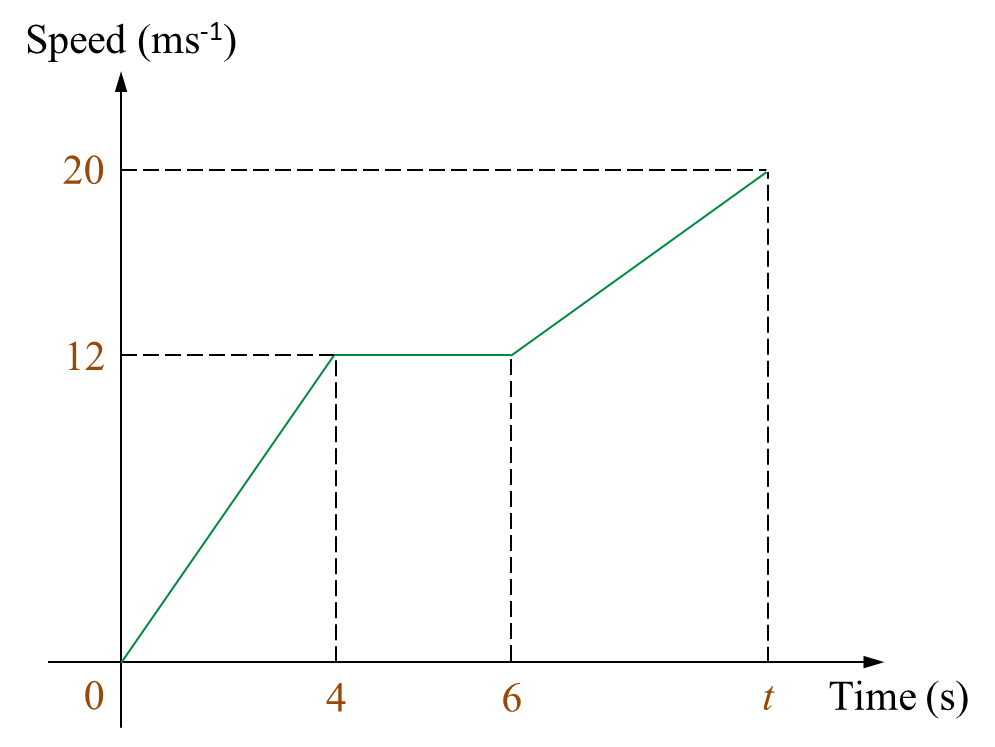 Diagram 11
Diagram 11