7.5.4 Energy Efficiency

Posted on April 17, 2020 by user

Efficiency of Electrical Appliance

The efficiency of an electrical appliance is given by the following equation eq1
Normally, the efficiency of an electrical appliance is less than 100% due to the energy lost as heat and the work done against friction in a machine.

Example 1
A lamp is marked “240V, 50W”. If it produces a light output of 40W, what is the efficiency of the lamp?

Answer:

Example 2
An electric motor raises a mass of 2kg to a height of 5m in 10s. If the input current from a source of 12V is 2A, find the efficiency of the electric motor.

Answer:
Input power,
P = IV
P = (2)(12) = 24W

Output power

Steps to Save Electricity

Use efficient lighting
Buy efficient electric appliances.
Use appliances with automatic power off function.
Choose electrical appliances of sizes and features which best suit your needs.
Proper utilization of all electrical appliances
1. Defrost refrigerators regularly
2. Run your washing machine only when it is fully loaded & Iron your clothes only when you have at least a few pieces to iron.
3. Regular cleaning of air filters in air-condition units and clothes dryers.

7.5.3 Power Rating and Energy Consumption

Posted on April 17, 2020 by user

Power Rating

Figure above is an example of power rating label.
An electrical appliance which is marked 240V, 1200W means that the electrical appliance will consume 1200J of energy in every second if the potential difference across it is 240V.

Example
A bulb rated 240V/80W is operated from a 120V power source. Find the resistance and the current flows through it.

Answer:

The current flows through the bulb

Energy Consumption

Calculating the cost of electricity consumption

The amount of electrical energy consumed in a given time:
The larger the power rating in the electrical appliance, the higher energy is used for every second.
The longer the usage time, the higher electrical energy is consumed.
The cost of electricity consumption is based on the number of kilowatt-hours (kWh) of electrical energy used.
The kilowatt-hours are sometimes known as the domestic units of electricity.
The kilowatt-hour (kWh) is the energy used by a device at a rate of 1000 watts in one hour.
1 kWh = (1000 W) × (60 × 60 s) = 3.6 MJ

Example:
If TNB charges 22 cents for each kWh of electrical energy used, calculate the total cost of using a 2kW electric kettle for 15 minutes and a 20 W filament bulb for 8 hours.

Answer:
Electrical energy consumed by the kettle,

Electrical energy consumed by the bulb,

Total energy consumed,

Cost = 0.66 x 22 cent = 14.52 cent

7.5.2 Power

Posted on April 17, 2020 by user

The electric power, P is defined as the rates of energy that supply to the circuit ( or the rates of work been done ) by sources of electric.
The unit of electric power is the watt (W).
One watt of power equals the work done in one second by one volt of potential difference in moving one coulomb of charge.
The electrical power of an electric circuit component can be find from the following equations:
Where
P = power/4
t = time
I = current
V = potential difference
R = resistance

Example 1:
A current of 0.50A flows through a 100Ω resistor. What is the power lost in the resistor?

Answer:

Example 2
An electric iron has a heating element of resistance 50Ω. If the operating current flowing through it is 4A, calculate the heat energy produced in 2 minutes.

Answer:
Power of the iron,

Heat energy produced,

Example 3
What is the power dissipated in a 4Ω light bulb connected to a 12V battery? What is the power dissipated in a 2Ω light bulb connected to the same battery? Which bulb is brighter?

Answer:
Assume that the bulbs are resistor

Power dissipated in the 4Ω resistor,

Power dissipated in the 2Ω resistor,

The power of the 2Ω bulb is higher, hence it is brighter.

[Conclusion: The lower the load resistance in a circuit, the greater the power dissipated in the circuit]

Example 4

An ideal battery with e.m.f. 12 V is connected in series to two bulbs with resistances R₁ = 4Ω and R₂ = 2Ω What is the current in the circuit and the power dissipation in each bulb?

Answer:
Potential difference across the 2 resistors, V = 12V
Equivalence resistance of the 2 resistors, R = 4 + 2 = 6Ω
Current in the circuit,

Power dissipated in R₁

Power dissipated in R₂

[Conclusion: In a series connection, the greater the resistance of a resistor, the greater the power dissipated]

Example 5

The figure above shows that an ideal battery is connected in parallel to two resistors with resistances 2Ω and 4Ω. Find the power dissipated in
a. the 4Ω resistor
b. the 2Ω resistor

Answer:
a. The potential difference across the 2 resistor = 12V
The power of the 2Ω resistor,

b.
The power of the 4Ω resistor,

[Conclusion: In a parallel connection, the lower the resistance, the greater the power of the resistor.]

In a circuit of any connection (series or parallel), the power dissipated in the whole circuit is equal to the sum of the power dissipated in each of the individual resistor.

Example 1:
2 identical bulb of resistance 3Ω is connected to an e.m.f. of 12V. Find the power dissipated in the circuit if
a. the bulb is connected in series
b. if the bulb is connected in parallel

Answer:
a.

Current pass through the 2 resistors,

Power of each of the resistor,

Sum of the power,

Potential difference across the 2 resistor = 12V
Power of each of the resistor,

Sum of the power,

Example 2:
A 800W heater is used to heat 250 cm³ of water from 30 to 100°C. What is the minimum time in which this can be done? [Density of water = 1000kg/m³; Specific Heat Capacity of water = 4200J°C^-1 kg^-1]

Answer:
Energy supply by the heater, E = Pt

Heat energy absorbed by the water, E = mcθ

Let's assume that all the energy supplied by the heater is converted to heat energy and absorbed by the water, hence

7.5.1 Electrical Energy

Posted on April 17, 2020 by user

From the definition of potential difference, the electrical work done is given by the equation W = QV, where
W = work
Q = charge
V = potential difference

Since the work done must be equal to the energy to do the work, therefore we can also say that, the electrical energy ( E ) is also given by the formula

Example
Given that the potential difference across a bulb is 240V and the current that flow through the bulb is 0.25A. Find the energy dissipated in the bulb in 30s.

Answer:
Formula of current,
E = QV
hence
Q = It

Energy dissipated,

E = QV
E = (It)Q
E = (0.25)(30)(240)
E = 1800V

7.4.2 Internal Resistance

Posted on April 17, 2020 by user

The internal resistance of a source (cell or generator) is the resistance against the moving charge in the source.

Load Resistance

The load resistance in a circuit is the effective resistance against the moving charge outside the source of electric.

Terminal Potential Difference

Terminal potential difference or terminal voltage is the potential difference across the two terminal (the positive terminal and the negative terminal) of an electric source (cell or generator).

Internal Resistance and Potential Difference Drop

If the internal resistance is ignored, the terminal potential difference is equal to the e.m.f.
If the internal resistance is present, the terminal potential difference will be lower than the e.m.f.
The relationship between e.m.f. and the terminal potential difference is given by the following equation.
Equation

E = V + Ir

or

E = IR + Ir

E = e.m.f.
V = terminal potential difference
I = current flows in the circuit
r = internal resistance
R = the load resistance

Example 1:
A cell has internal resistance 0.5Ω and the potential difference across the cell is 4V when a 2A current flows through it. Find the e.m.f. of the cell.

Answer:
r = 0.5Ω
V = 4V
I = 2A
E = ?

E = V + Ir
E = (4) + (2)(0.5)
E = 5V

Example 2:

A cell with e.m.f. 3V and internal resistance, 1Ω is connected to a 5Ω resistor, and a voltmeter is connected across the resistor as shown in the diagram on the left. Find the reading of the voltmeter.

Answer:
E = 3V
r = 1Ω
R = 5Ω
V = ?

E = I(R + r)
(3) = I(5 + 1)
3 = 6I
I = 3/6 = 0.5A

V = IR
V = (0.5)(5)
V = 2.5V

Measuring e.m.f. and Internal Resistance

Three methods can be used to measure the e.m.f. and internal resistance.

Open circuit-Close circuit
Simultaneous equation
Linear Graph

Open Circuit

In open circuit ( when the switch is off), the voltmeter shows the reading of the e.m.f.

Close Circuit

In close circuit ( when the switch is on), the voltmeter shows the reading of the potential difference across the cell.

With the presence of internal resistance, the potential difference across the cell is always less than the e.m.f..

Example 1:

The diagram above shows a simple circuit that connect some baterries to a resistor. The voltmeter shows a reading of 5.0V when the switch is off and 4.5V when the switch is on. What are the e.m.f. and the internal resistance of the cell?

Answer:
When the switch is off, the reading of the voltmeter shows the e.m.f. of the batteries. Therefore.
e.m.f. = 5.0V

When the switch in turned on, the reading of the voltmeter shows the potential difference of the resistor. Therefore,
V = 4.5V

The current that pass through the resistor,

E = V + Ir
(5.0) = (4.5) + I(0.5)
0.5I = 5.0 - 4.5
I = 0.5/0.5
I = 1A

Example 2:

Diagram (a)

Diagram (b)

A cell is connected to a circuit as shown in diagram (a). The graph in diagram (b) shows the change of the reading of the voltmeter, V against time, t. If t is the time where the switch is close, find
(a) the e.m.f. of the cell
(b) the internal resistance of the cell.

Answer:
(a) Before the switch turned on, the reading of the ammeter shows the e.m.f. of the cells.

From the graph, the e.m.f. = 3.0V

(b)
e.m.f., E = 3.0V
Potential difference across the resistor, V = 2.5V

Current that pass through the resistor,

7.4.1 Electromotive Force

Posted on April 17, 2020 by user

In a circuit, electromotive force is the energy per unit charge converted from the other forms of energy into electrical energy to move the charge across the whole circuit.
In equation,
where
E = e.m.f.,
W = energy converted from non-electrical forms to electrical form
Q = positive charge.

The unit of e.m.f. is JC^-1 or V (Volt)
The unit of e.m.f. is JC^-1 or V (Volt). Electromotive force of 1 Volt means that 1 Joule of electrical energy is supplied to the circuit to move 1 Coulomd of charge across the whole circuit.

Electromotive Force	Potential Difference
Similarities: Have same unit (Volt) Can be measured by Voltmeter
Definition The electromotive force (e.m.f.) is defined as the energy per unit charge that is converted from chemical, mechanical, or other forms of energy into electrical energy in a battery or dynamo.	Definition The potential difference (p.d.) between two points is defined as the energy converted from electrical to other forms when one coulomb of positive charge passes between the two points.
Symbol: Denote by the symbol, E.	Symbol: Denote by the symbol, V

Example 1
When a 1Ω resistor is connected to the terminal of a cell, the current that flow through it is 8A. When the resistor is replaced by another resistor with resistance 4Ω, the current becomes 2⅔A. Find the
a. internal resistance of the cell
b. e.m.f. of the cell

Answer:
Experiment 1
R₁ = 1Ω
I₁ = 8A

Experiment 2
R₂ = 4Ω
I₂ = 2⅔A

Solve the simultaneous equation
E = 12V, r = 0.5Ω

Example 2
The diagram on the left shows that the terminal potential difference of a batteries is 1.2V when a 4 Ω resistor is connected to it. The terminal potential become 1.45V when the resistor is replaced by another resistor of resistance 29Ω
Find the
a. internal resistance, r
b. e.m.f. of the batteries.
Answer:
Experiment 1

V₁ = 1.2V
R₁ = 4Ω

I = V/R
I = (1.2)/(4)
I = 0.3A

E = V + Ir
E = (1.2) + (0.3)r
E - 0.3r = 1.2 ------------(eq1)

Experiment 2
V₂ = 1.45V
R₂ = 29

I = V/R
I = (1.45)/(29)
I = 0.05A

E = V + Ir
E = (1.5) + (0.05)r
E - 0.05r = 1.45 -----------------(eq2)

Solve the simultaneous equation eq1 and eq2

E = 1.5V, r = 1Ω

The Linear Graph

From the equation,

E = V + Ir

Therefore

V = -rI + E

Y axis = Potential difference (V)
X axis = Current (I)
Gradient od the grapf, m = - internal resistance (r)
Y intercept of the graph, c = e.m.f.

Example:

The graph shows the variation of potential difference with current of a battery.
What is the internal resistance and e.m.f. of the battery?

Answer:
e.m.f. = y-intercept = 3V

internal resistance,
r = -gradient of the graph
r = - (-3)/(6) = 0.5Ω

7.3.3 Current and Potential Difference

Posted on April 17, 2020 by user

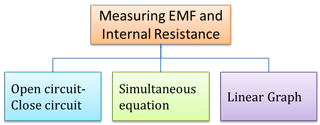
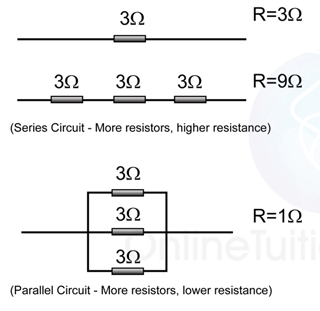
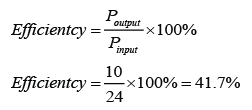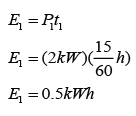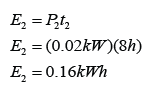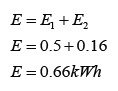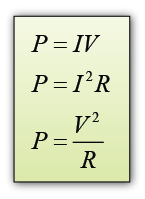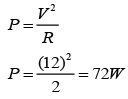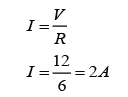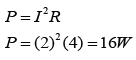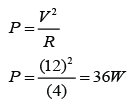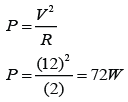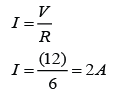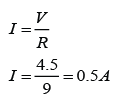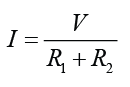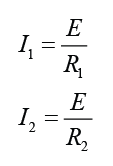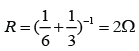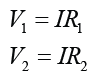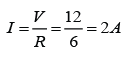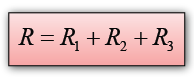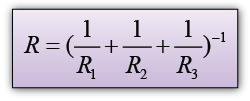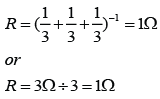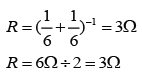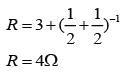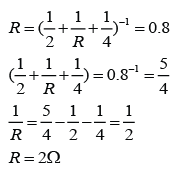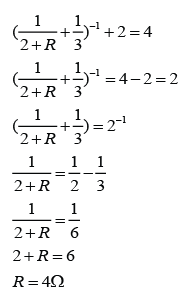Series Circuit

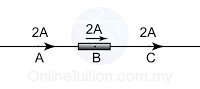
The current flow into a resistor = the current flow inside the resistor = the current flows out from the resistor

I_A = I_B = I_C

In a series circuit, the current at any points of the circuit is the same.

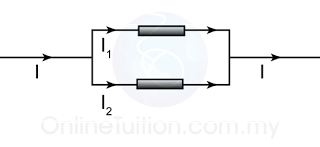
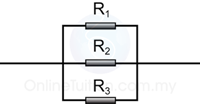
Parallel Circuit

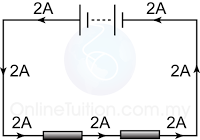
The current flow into a parallel circuit is equal to the sum of the current in each branches of the circuit.

I = I₁ + I₂

Example

If the resistance of the 2 resistors is the same, current will be divided equally to both of the resistor.

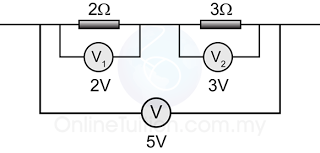
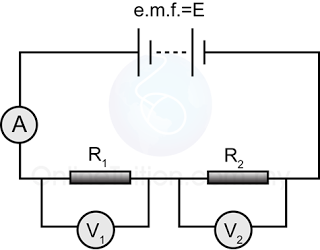
Series Circuit

The sum of the potential difference across individual resistor in between 2 points in a series circuit is equal to the potential difference across the two points.

V = V₁ + V₂

Example

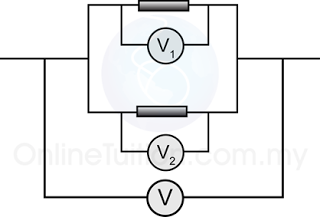
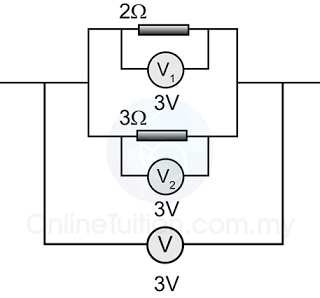
Parallel Circuit

The potential difference across all resistors in a parallel circuit is the same.

V = V₁ = V₂

Example

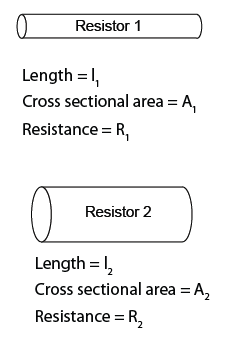
Finding Current in a Series Circuit

In a series circuit, the current flow through each of the resistor is equal to the current flows through the whole circuit.
Potential difference (V) across the whole circuit is equal to the e.m.f. (E) if the internal resistance is ignored.
Effective resistance for the whole circuit = R₁ + R₂
By Ohm’s Law

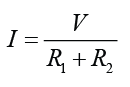
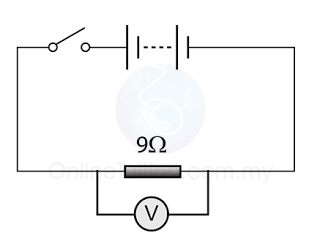
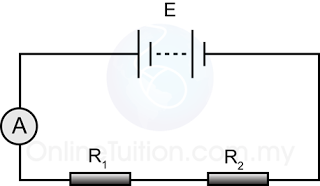
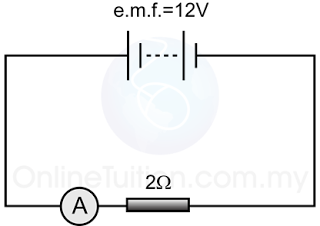
Example 1

For the circuit in the diagram above,

find the reading of the ammeter.
find the current flows through the resistor.

Answer:
a.
Potential difference across the 2Ω resistor, V = 12V
Resistance, R =2Ω

V = IR
(12) = I(2)
I = 12/2 = 6A
b.
The current flows through the resistor
= the reading of the ammeter
= 6Ω

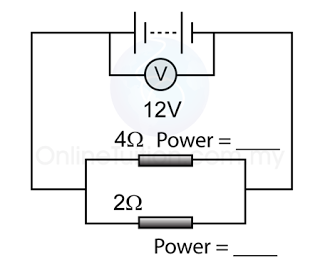
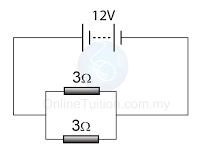
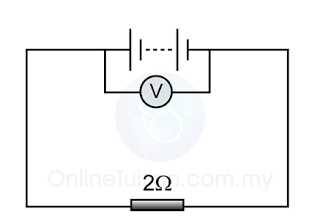
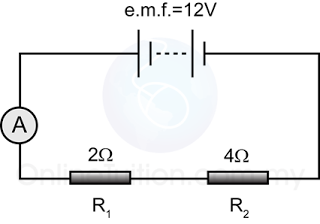
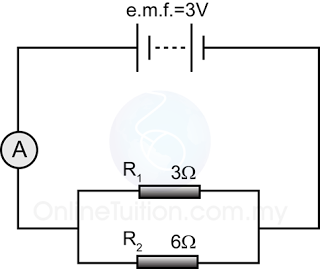
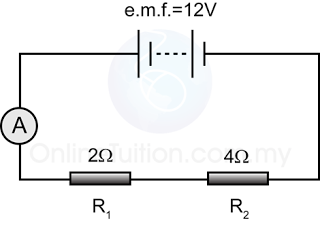
Example 2

For the circuit above,

find the reading of the ammeter.
find the current flows through each of the resistors.

Answer:
a.
Potential difference across the 2 resistors, V = 12V
The equivalent resistance of the 2 resistors, R =6Ω

V = IR
(12) = I(6)
I = 12/6 = 2A

b.
The current flows through the resistors
= the reading of the ammeter
= 2Ω

Finding Current in a Parallel Circuit

In parallel circuit, the potential difference (V) across each of the resistors is equal to the e.m.f. (E) if the internal resistance of the cell is ignored.

By Ohm’s Law

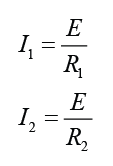
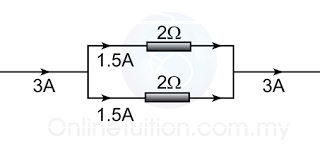
Example 1:

For the diagram above,
a. find the reading of the ammeter.
b. find the current in each of the resistors.

Answer:
a.
Effective resistance of the 2 resistors in parallel

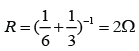
Potential difference across the 2 resistance, V = 3V
V = IR
(3) = I(2)
I = 3/2 = 1.5A

Reading of the ammeter = 1.5A
b.
Current in the 3Ω resistor,
V = IR
(3) = I(3)
I = 3/3 = 1A

Current in the 6Ω resistor,
V = IR
(3) = I(6)
I = 3/6 = 0.5A

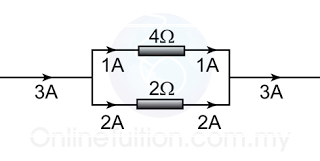
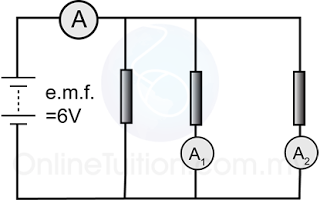
Example 2

Figure above shows 3 identical resistors connected in parallel in a circuit. Given that the resistance of the resistors are 6Ω each. Find the reading of all the ammeters in the figure above.
Answer:
The potential diffrence across the resistors V = 6V
For ammeter A,
The equivalent resistance = 6/3 = 2Ω.
V = IR
(6) = I(2)
I = 6/2 = 3A

For ammeter A₁,
V = IR
(6) = I(6)
I = 6/6 = 1A

For ammeter A₂,

V = IR
(6) = I(6)
I = 6/6 = 1A

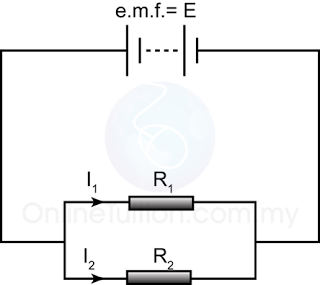
Finding Potential Difference in a Series Circuit

In the circuit above, if the current in the circuit is I, then the potential difference across each of the resistor is

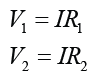
Example

Find the potential difference across each of the resistors in the diagram above.

Answer:
The potential difference across the 2 resistors, V = 12V
The equivalent resistance of the 2 resistors, R = 2 + 4 = 6Ω
Current pass through the 2 resistor,

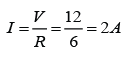
For resistor R₁,
V = IR
V = (2)(2) = 4V

For resistor R₂
V = IR
V = (2)(4) = 8V

7.3.2 Resistance in Series and Parallel Circuit

Posted on April 17, 2020 by user

In a series circuit, the effective resistance is equal to the sum of the individual resistance, as shown in the following equation.
In a parallel circuit, the effective resistance of the resistors can be calculated fro the following equation.

Example:

Find the equivalent resistance of the connection shown in the diagram above.

Answer:
(a)
R = 2 + 3 + 6 = 11Ω

(b)

(c)

(d)

In a series circuit, the more resistors with equal resistance in the circuit, the higher the effective resistance of the circuit.
In a parallel circuit, the more resistors with equal resistance in the circuit, the lower the effective resistance of the circuit.

Finding the Resistance of an Individual Resistor

Example

Given that the equivalent resistance of the connection in the figure above is 0.8Ω, find the resistance of the resistor R.

Answer:

Example

Given that the equivalent resistance of the connection in the figure above is 4Ω, find the resistance of the resistor R.

Answer:

7.3.1 Series Circuit and Parallel Circuit

Posted on April 17, 2020 by user

The resistors connected in one non-branched wire is said to be connected in series, whereas resistors connected in a branched wire is said to be connected in parallel.
In the diagram above, (a), (b) and (c) are series circuit whereas (d), (e) (f) and (g) are parallel circuit.

7.2.4 Factors Affecting the Resistance in a Conductor

Posted on April 17, 2020 by user

The resistance R of a given conductor depends on:

its length l,
its cross-sectional area A
its temperature and
the type of material.

Length

Resistance is directly proportional to the length of the conductor.

Cross Sectional Area

Resistance is inversely proportional to the cross sectional area of the conductor.

Temperature

A conductor with higher temperature has higher resistance.

Material

Difference materials have difference resistivity. The resistance of copper wire is lower than iron wire.

Since resistance is directly proportional to the length and inversely proportional to the cross sectional area of the conductor. If two resistors of same material have same temperature, we can relate the resistance of the two resistors by the following equation.