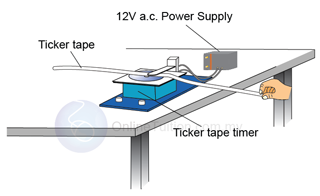
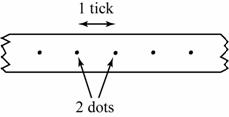
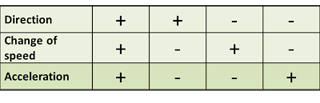
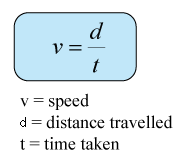
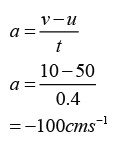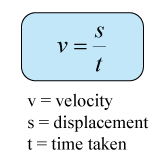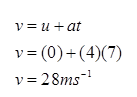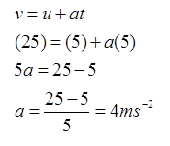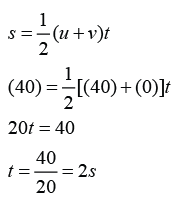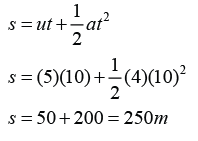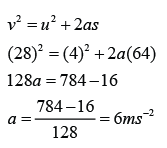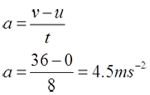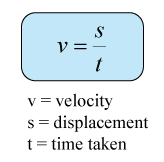Finding Acceleration
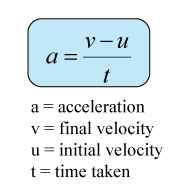
Acceleration of a motion can be determined by using ticker tape through the following equation: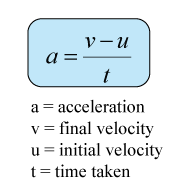
Caution!:
t is time taken from the initial velocity to the final velocity.
Example:
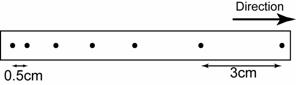
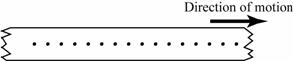
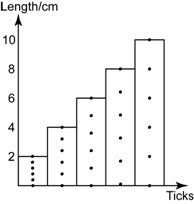
The ticker-tape in figure above was produced by a toy car moving down a tilted runway. If the ticker-tape timer produced 50 dots per second, find the acceleration of the toy car.
Answer:
In order to find the acceleration, we need to determine the initial velocity, the final velocity and the time taken for the velocity change.
Initial velocity,
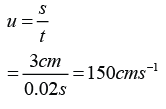
Final velocity,
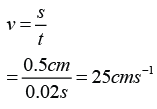
Time taken for the velocity change,
t = (0.5 + 4 + 0.5) ticks = 5 ticks
t = 5 × 0.02s = 0.1s
Acceleration,
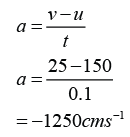
Example:
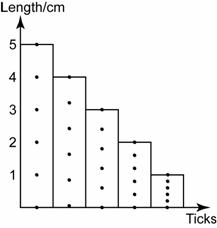
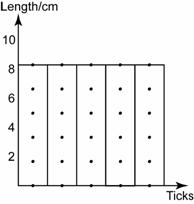
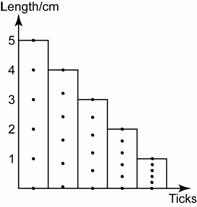
A trolley is pushed up a slope. Diagram above shows ticker tape chart that show the movement of the trolley. Every section of the tape contains 5 ticks. If the ticker-tape timer produced 50 dots per second, determine the acceleration of the trolley.
Answer:
In order to find the acceleration, we need to determine the initial velocity, the final velocity and the time taken for the velocity change.
Initial velocity,
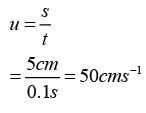
Final velocity
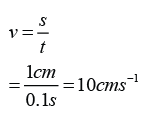
Time taken for the velocity change,
t = (2.5 + 5 + 5 + 5 + 2.5) ticks = 20 ticks
t = 20 × 0.02s = 0.4s
Acceleration,