Home › SPM Physics › Archive for Heat

Heat

4.4.4 Pressure Law

Posted on by

Pressure law states that for a fixed mass of gas, the pressure of the gas is directly proportional to the absolute temperature of the gas provided the volume of the gas is kept constant.


Formula:


Explanation

  1. The kinetic energy of gas molecules increases with temperature.
  2. The air molecules collide with the wall of the container at higher velocity and frequency.
  3. The pressure in the gas increases, causing an increase in volume.

Graph

  1. In the graphs above, the first graph shows that P is directly proportional to the absolute temperature.
  2. The second graph shows that, if the temperature is in °C, the graph does not pass through the origin.
  3. The third and the forth graphs shows that P/T is always constant for all value of P and T.


Example 2:
An iron cylinder containing gas with pressure 200kPa when it is kept is a room of temperature 27°C. What is the pressure of the gas when the cylinder is located outdoor where the temperature is 35°C.

Answer:
P1 = 200kPa
T1 = 273 + 27 = 300K
P2 = ?
T2 = 273 + 35 = 308K

 

4.4.3 Charles’ Law

Posted on by

Charles’ law states that for a fixed mass of gas, the volume of the gas is directly proportional to the absolute temperature of the gas provided the pressure of the gas is kept constant.


Formula:

Explanation

  1. When temperature increases, the average kinetic energy of the gas particles will increase.
  2. The air molecule move faster and collide with the wall of the container more vigorously at higher frequency.
  3. As a result, the space between the gas particles increases and the volume of the gas increases.

Graph

  1. In the graphs above, the first graph shows that V is directly proportional to the absolute temperature.
  2. The second graph shows that, if the temperature is in oC, the graph does not pass through the origin.
  3. The third and the forth graphs shows that V/T is always constant for all value of V and T.
Example 3:


The figure shows some air trapped in a capillary tube. Given that the temperature of the air is 27°C. Find the length of the air column when the temperature of the air is increased to 87°C.

Answer:
V1 = 6cm
T1 = 273 + 27 = 300K
V2 = ?
T2 = 273 + 87 = 360K

 

4.4.2 Boyle’s law

Posted on by

Boyle's law states that the pressure of a gas with constant mass is inversely proportional to its volume provided the temperature of the gas is kept constant.


Formula:

Explanation 

  1. When the volume of gas decreases, the number of gas particles per unit volume increases.
  2. As a result, the frequency of collision between the air particles and the wall of the container increases.
  3. As such, the pressure of the gas increases.

Graph

  1. In the graphs above, the first graph shows that P is inversely proportional to V. 
  2. The second graph shows that P is directly proportional to 1/V. 
  3. The third and the forth graphs shows that PV is always constant for all value of V and P.

Example 1:
A fish releases a bubble of air of volume 1cm³ at the bottom of a lake. The depth of the lake is 10m. Find the volume of the bubble when it reaches the surface of the pond. (Assume that the atmospheric pressure is equal to 10m of water)

Answer:
V1 = 1cm³
P1 = 20m water
V2 = ?
P2 = 10m water


 

4.4.1 Pressure, Temperature and Volume of Gas

Posted on by

The kinetic theory of gases explains the the relationship between the pressure, temperature and volume of gases base on the following assumptions:

  1. The gas consists of very small particles, each of which has a mass.
  2. These particles are in constant, random motion.
  3. The rapidly moving particles constantly collide with each other and with the walls of the container. All these collisions are perfectly elastic.
  4. There are forces of attraction between particles of matter. These attraction forces will increase as the distance between the particles becomes closer.
  5. The average kinetic energy of the gas particles depends only on the temperature of the system. The higher the temperature, the higher the kinetic energy of the particles.

 

4.3.7 Cooling by Evaporation

Posted on by

  1. Blowing air into a liquid will cause the liquid evaporate faster.
  2. During evaporation, latent heat is absorbed from the liquid (as a surrounding) causing the temperature of the liquid decreases.

Applications of Cooling by Evaporation

Refrigerators

  1. The cooling effect in many refrigerators is produced by the evaporation of a volatile liquid called Freon.
  2. The liquid Freon evaporates rapidly in the pipes in the freezer compartment as more and more of its vapour is drawn away by the electric pump. As the Freon evaporates, it draws the necessary latent heat from the food inside the refrigerator.
  3. The pump compresses the vapour which turns liquid again on being forced through the zig-zag pipe at the back of the refrigerator. The latent heat released is given off through the cooling fins.
  4. In this way, thermal energy is extracted from the food inside the refrigerator and given out at the back. A refrigerator actually makes your kitchen warmer.

 

 

4.3.6 Evaporation and Boiling

Posted on by

Rate of Evaporation

  1. Evaporation is the process of converting a substance (such as water) from its liquid state to its gaseous state at temperature lower than the boiling point of the liquid.
  2. There are several ways of making a liquid evaporate faster:
    1. Increase its temperature 
    2. Increase its surface area 
    3. Pass air through it or across its surface 
    4. Make the liquid into a fine spray
      A spray is made up of millions of tiny liquid droplets with a very large total surface area. The highly curved surfaces make it easier for molecules to escape.

 

4.3.5 Specific Latent Heat of Vaporisation

Posted on by

Measuring the Specific Latent Heat of Vaporization of Water

  1. Figure above shows the apparatus used. When the water in the can is boiling vigorously, the mass reading on the balance is noted and a stopwatch started. A few minutes later, the stopwatch is stopped and the mass reading is taken again.
  2. The difference in the mass readings gives the mass of water which has been changed into steam during the time measured.
    Therefore, the specific latent heat of vaporisation of water can be calculated by the following equation
Note:
  1. The boiling point of a liquid is proportional to the air pressure of the surrounding. The higher the air pressure, the higher the boiling point.
  2. At higher altitude, the atmospheric pressure is lower. Therefore the boiling point of a liquid will decrease at higher altitude.

Pressure Cooker

  1. Pressure cooker can cook faster than normal cooker.
  2. The high gas pressure inside the pressure cooker increases the boiling point of the liquid in the pressure cooker.
  3. As a result, the food is cooked under higher temperature. More heat is supplied to the food, hence make cooking faster.
  4. The function of the safety valve is to release extra steam to the surrounding and consequently reduce the pressure in the pressure cooker when it is too high.

 

4.3.4 Specific Latent Heat

Posted on by
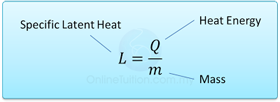
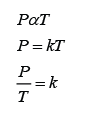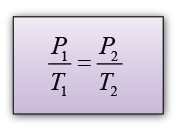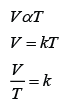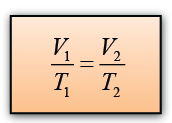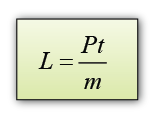  1. The specific latent heat of a substance is the amount of heat requires to change the phase of 1 kg of substance at a constant temperature.
  2. Specific latent heat is measured in J/kg, if energy is measured in J and mass in kg.For example, specific latent heat of ice is 334000J/kg means 334000 J of energy is needed to convert 1kg of water into ice or vice versa.
    Formula:
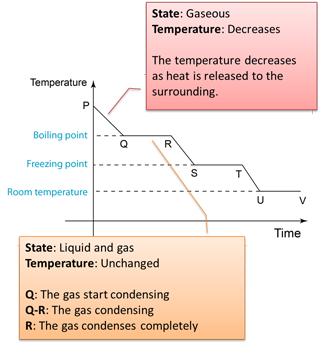
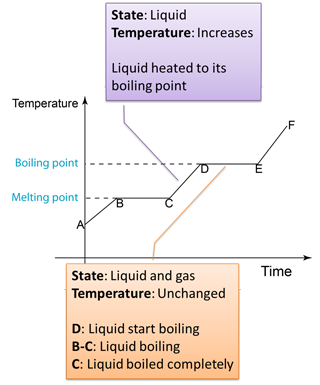
  3. The specific latent heat of vaporization is the heat needed to change 1 kg of a liquid at its boiling point into vapour without a change in temperature.
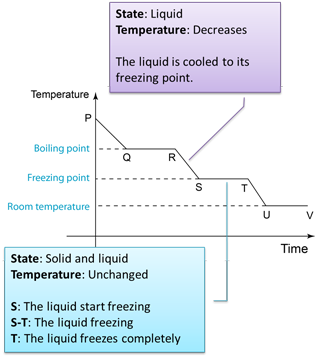
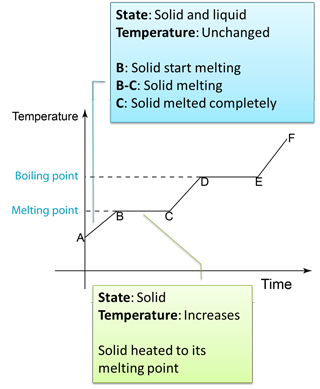
  4. The specific latent heat of fusion is the heat needed to change 1 kg of a solid at its melting point into a liquid, without a change in temperature.
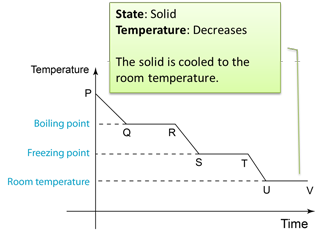
  5. If any solid is to become a liquid, it must gain the necessary latent heat. Equally, if a liquid is to change back into a solid, it must lose this latent heat.

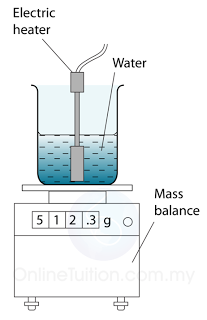
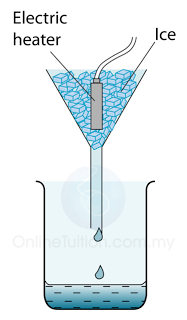
Measuring the Specific Latent Heat of Fusing of Ice

  1. Figure above shows the apparatus setup to determine the specific latent heat of fusion of ice. Some ice at 0 °C is heated by a small electric heater which is left switched on for several minutes. 
  2. Some of the ice melts to form water which runs down through the funnel and is collected in the beaker. 
  3. The mass of ice (m) melted is found by measuring the mass of water collected.
  4. If the power of the heater is P and the time taken to heat the ice = t, then the thermal energy supplied by the heater = thermal energy used to melt ice = Pt.
    Therefore, the specific latent heat of fusion of ice

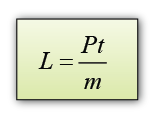
Precaution Steps:

  1. The heating element of the heater must fully immerse in ice so that all the heat generated is absorbed by the ice.
  2. A control set is needed to estimate the amount of mass of ice melted by the heat from the surrounding.

Note:

  1. The heat received by ice is less than the calculated value Pt as some heat is lost to the surrounding. This will result in the value of l obtained from the calculation to be slightly higher than the standard value.
  2. If impurity is present in water, the melting point of the water will be lower than normal.

Example 1:
How much heat energy is required to change 2 kg of ice at 0°C into water at 20°C? [Specific latent heat of fusion of water = 334 000 J/kg; specific heat capacity of water = 4200 J/(kg K).]

Answer:
m = 2kg
Specific latent heat of fusion of water, L = 334 000 J/kg
specific heat capacity of water = 4200 J/(kg K)

Energy needed to melt 2kg of ice,
Q1 = mL = (2)(334000) = 668000J

Energy needed to change the temperature from 0°C to °C.
Q2 = mcθ  = (2)(4200)(20 - 0) = 168000J

Total energy needed = Q1 + Q2 = 668000 + 168000 = 836000J


Example 2:
Starting at 20°C, how much heat is required to heat 0.3 kg of aluminum to its melting point and then to convert it all to liquid? [Specific heat capacity of aluminium = 900J kg-1 °C-1; Specific latent heat of aluminium = 321,000 Jkg-1, Melting point of aluminium = 660°C]

Answer:
m = 0.3kg
Specific latent heat of fusion of aluminium, L = 321 000 J/kg
specific heat capacity of aluminium = 900 J/(kg K)

Energy needed to increase the temperature from 20°C to 660°C
Q1 = mcθ  = (0.3)(900)(660 - 20) = 172,800J

Energy needed to melt 0.3kg of aluminium,
Q2 = mL = (0.3)(321000) = 96,300J

Total energy needed = Q1 + Q2 = 172,800 + 96,300 = 269,100J



Example 3:
How much heat must be removed by a refrigerator from 2 kg of water at 70 °C to convert it to ice cubes at -11°C? [Specific heat capacity of water = 4200J kg-1 °C-1; Specific latent heat of fusion of ice = 334,000 Jkg-1, specific heat capacity of ice = 2100 J/(kg K)]

Answer:
m = 2kg
Specific latent heat of fusion of water, L = 334,000 J/kg
Specific heat capacity of water, cw = 4,200 J/(kg K)
Specific heat capacity of ice, ci = 2,100 J/(kg K)

Energy to be removed to reduce the temperature from 70°C to 0°C (Freezing point of water)
Q1 = mcθ  = (2)(4200)(70 - 0) = 588,000J

Energy needed to freeze 2kg of water,
Q2 = mL = (2)(334,000) = 668,000J

Energy to be removed to reduce the temperature from 0°C to -11°C
Q3 = mcθ  = (2)(2100)(0 - (-11)) = 46,200J

Total energy needed = Q1 + Q2  + Q3 = 588,000 + 668,000 = 46,200J = 1,302,200J

 

4.3.3 Cooling Curve

Posted on by

Figure below shows the change of the temperature when a gas is cooled to become solid.


Q & A

Q: Why the temperature remained unchanged from Q-R and S-T?

A: The temperature remains unchanged because the heat released during the formation of the intermolecular forces compensates the heat losses to the surrounding.

Q & A

Q: Why the temperature remained unchanged from U-V?

A: Because the temperature of the solid has reached the temperature of the surrounding.

 

 

4.3.2 Heating Curve

Posted on by

Figure below shows the change of the temperature when a solid is heated until it become gas.


Note:
B to C
  1. Temperature remain unchanged because the heat absorbed is used to overcome the force between the particles in the solid.
  2. The heat absorbed to change a solid to liquid is called the latent heat of fusion.

D to E
  1. Temperature remain unchanged because the heat absorbed is used to overcome the force between the particles in the liquid and also the atmospheric pressure.
  2. The heat absorbed to change a liquid to gas is called the latent heat of vaporisation.