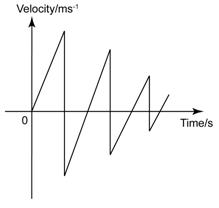
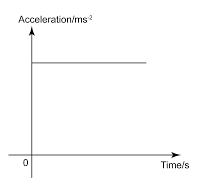
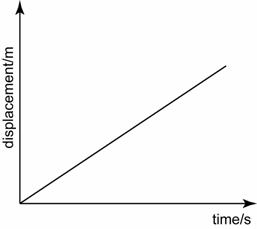
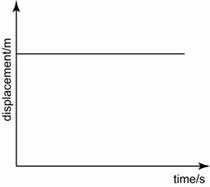
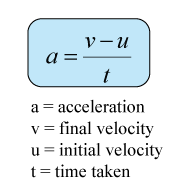
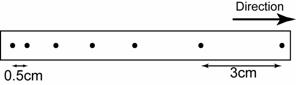
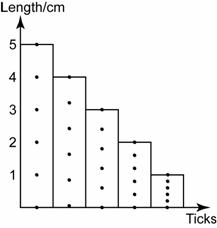
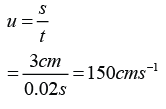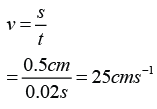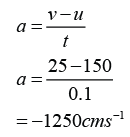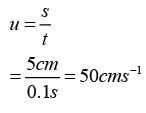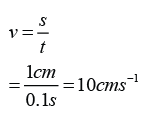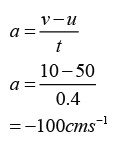- A force is push or pull exerted on an object.
- Force is a vector quantity that has magnitude and direction.
- The unit of force is Newton ( or kgms-2).
Unbalanced Force/ Resultant Force
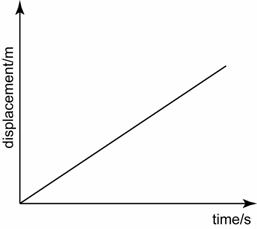
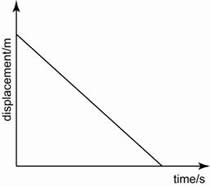
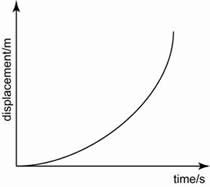
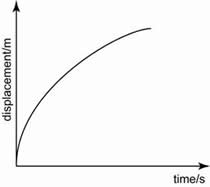
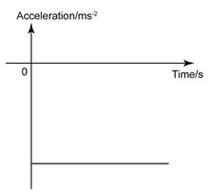
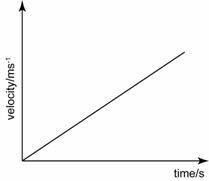
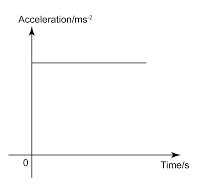
When the forces acting on an object are not balanced, there must be a net force acting on it. The net force is known as the unbalanced force or the resultant force.When a force acts on an object, the effect can change the
- size,
- shape,
- stationary state,
- speed and
- direction of the object.
Types of Forces
Friction
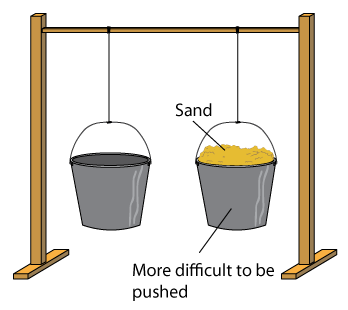
- Friction is the force that oppose motion.
- There are 2 types of friction that you need to know in SPM:
- Static friction - friction between 2 surfaces that are not moving relative to each other
- sliding friction - friction where an object slides or rubs against another surface.
- Video below discuss the differences between these 2 types of friction.
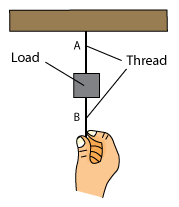
Tension

When a rope attached to an object is pulling on the object, the rope exerts a force T on the object, and the magnitude T of that force is called the tension in the rope.
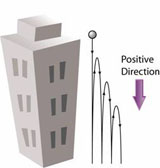
Weight (Gravitational Force)
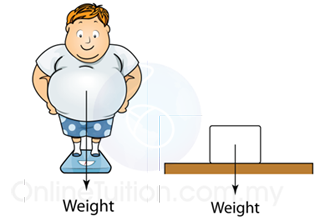
2. It is always point towards the centre of the earth.
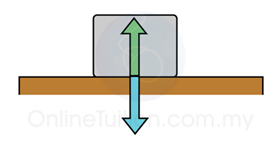
Normal Reaction (Normal Contact Force)

Normal reaction is a force acting perpendicular to two surfaces in contact with each other.
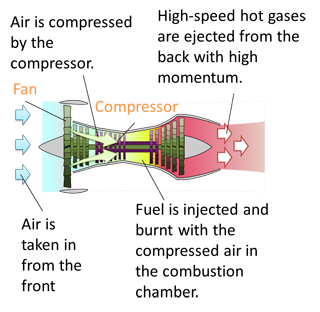
Newton’s Third Law of Motion
Newton's third law of motion states that for every force, there is a reaction force with the same magnitude but in the opposite direction.Examples
- When a man standing on the surface of the earth, his body is pulled by the gravitational force from the earth.
- According to Newton's Third Law of Motion, his body will also have another gravitational force that pull the earth towards him, with the same magnitude as the gravitational force of the earth, but in opposite direction.

(The earth pull the man, the man pull the earth.)
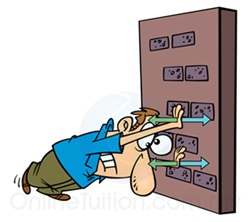
(The man push the wall, the wall push the man.)






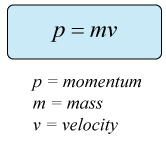







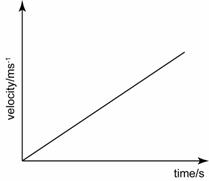
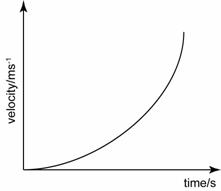

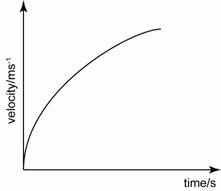

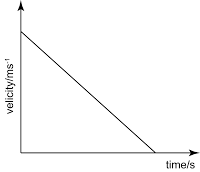


.png)