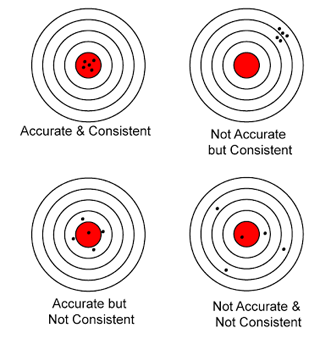
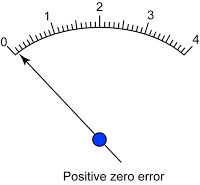
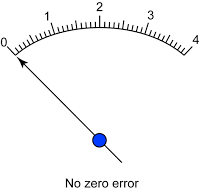
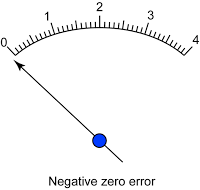
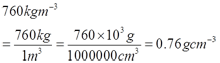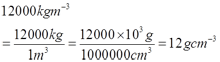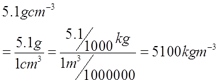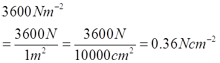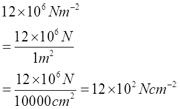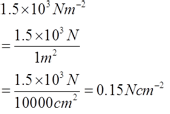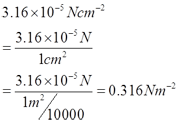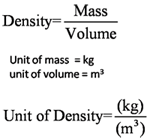Ruler

1. Make sure that the object is in contact with the ruler.
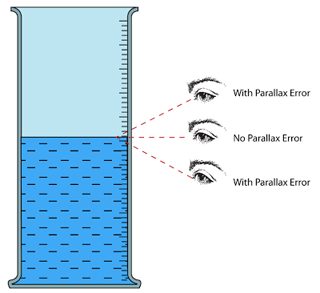
2. Avoid parallax error.
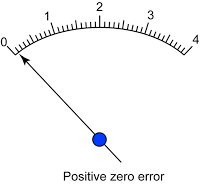
3. Avoid zero error and end error.

Thermometer

1. Thermometers of range -10°C - 110°C with accuracy 1°C.
2. Thermometers of range 0°C - 360°C with accuracy 2°C.

1. Make sure that the temperature measured does not exceed the measuring range.
2. When measuring temperature of liquid.
   1. immerse the bulb fully in the liquid
   2. stir the liquid so that the temperature in the liquid is uniform
   3. do not stir the liquid vigorously to avoid breaking the thermometer

Stopwatch

(The image is licienced under GDFL. The source file can be obtained at wikipedia.org.)

1. analogue stopwatches of sensitivity 0.1s or 0.2s
2. digital stopwatches of sensitivity 0.01s.

Consistency

1. Consistency (or precision) is the ability of an instrument in measuring a quantity in a consistent manner with only a small relative deviation between readings.
2. The consistency of a reading can be indicated by its relative deviation.
3. The relative deviation is the percentage of mean deviation for a set of measurements and it is defined by the following formula:

Accuracy

1. The accuracy of a measurement is the approximation of the measurement to the actual value for a certain quantity of Physics.
2. The measurement is more accurate if its number of significant figures increases.
3. Table above shows that the micrometer screw gauge is more accurate than the other measuring instruments.
   
4. The accuracy of a measurement can be increased by
   1. taking a number of repeat readings to calculate the mean value of the reading. 
   2. avoiding the end errors or zero errors. 
   3. taking into account the zero and parallax errors. 
   4. using more sensitive equipment such as a vernier caliper to replace a ruler. 
5. The difference between precision and accuracy can be shown by the spread of shooting of a target (as shown in Diagram below).

Sensitivity

1. The sensitivity of an instrument is its ability to detect small changes in the quantity that is being measured.
2. Thus, a sensitive instrument can quickly detect a small change in measurement.
3. Measuring instruments that have smaller scale parts are more sensitive.
4. Sensitive instruments need not necessarily be accurate.

1. Error is the difference between the actual value of a quantity and the value obtained in measurement.
2. There are 2 main types of error 
   1. Systematic Error 
   2. Random Error

Systematic Error

1. Systematic errors are errors which tend to shift all measurements in a systematic way so their mean value is displaced. Systematic errors can be compensated if the errors are known.
2. Examples of systematic errors are
   1. zero error, which cause by an incorrect position of the zero point, 
   2. an incorrect calibration of the measuring instrument. 
   3. consistently improper use of equipment. 
3. Systematic error can be reduced by
   1. Conducting the experiment with care.
   2. Repeating the experiment by using different instruments.
      

Zero error

1. A zero error arises when the measuring instrument does not start from exactly zero.
2. Zero errors are consistently present in every reading of a measurement.
3. The zero error can be positive or negative.

(NO ZERO ERROR: The pointer of the ammeter place on zero when no current flow through it.)

Random errors

1. Random errors arise from unknown and unpredictable variations in condition.
2. It fluctuates from one measurement to the next.
3. Random errors are caused by factors that are beyond the control of the observers.
4. Random error can cause by
   1. personal errors such as human limitations of sight and touch. 
   2. lack of sensitivity of the instrument: the instrument fail to respond to the small change. 
   3. natural errors such as changes in temperature or wind, while the experiment is in progress. 
   4. wrong technique of measurement. 
5. One example of random error is the parallax error. Random error can be reduced by 
   1. taking repeat readings 
   2. find the average value of the reading.

Parallax error

A parallax error is an error in reading an instrument due to the eye of the observer and pointer are not in a line perpendicular to the plane of the scale.

Prefixes are the preceding factor used to represent very small and very large physical quantities in SI units.

Table below shows the prefixes that you need to know in SPM.

Conversion of prefixes

Prefixes to Normal Number

Normal number to Prefixes

1. Scientific notation (also known as Standard index notation) is a convenient way to write very small or large numbers. 
2. In this notation, numbers are separated into two parts, a real number with an absolute value between 1 and 10 and an order of magnitude value written as a power of 10.

Significant Figure

1. In measurement, significant figures relate the certainty of the measurement.
2. As the number of significant figures increases, the certainty of the measurement increase, which means we are more certain about what we have measured.

Scalar Quantity

1. Scalars are quantities which are fully described by a magnitude alone. 
2. Magnitude is the numerical value of a quantity. 
3. Examples of scalar quantities are distance, speed, mass, volume, temperature, density and energy. 

Vector Quantity

1. Vectors are quantities which are fully described by both a magnitude and a direction. 
2. Examples of vector quantities are displacement, velocity, acceleration, force, momentum, and magnetic field.

Speed, density and pressure are derived quantities. When converting their units, firstly, we write the units in fraction form, then only do the unit convertion for the numerator and denominator.

SI unit

Derived Unit

1. The derived unit is a combination of base units through multiplying and/or dividing them.
2. For instance,  Speed is defined as the rate of distance change, and can be written in the mathematic form
   

Example:
Find the derived unit of density.

Answer:

Unit of Density = kg/m³

1. A derived quantity is a Physics quantity that is not a base quantity. It is the quantities which derived from the base quantities through multiplying and/or dividing them.
2. For example, speed is define as rate of change of distance, Mathematically, we write this as Speed = Distance/Time. Both distance and time are base quantities, whereas speed is a derived quantity as it is derived from distance and time through division.
   Example
   
   
   (Speed is derived from dividing distance by time.)
3. Belows are the derived quantities that you need to know in SPM. You need to know the equation of all the quantities, so that you can derive their unit from the equation.
4. If you find it difficult to memorise all these equation, you can skip it now because you are going to learn all of them in the other chapter. 

Physical Quantity

1. A physical quantity is a quantity that can be measured.
2. A physical quantity can be divided into base quantity and derived quantity.

Base Quantities

1. Base quantities are the quantities that cannot be defined in term of other physical quantity.
2. The base quantities and its units are as in the table below: