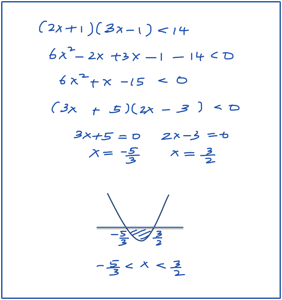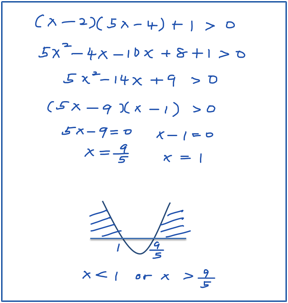Home › Archive for Uncategorized

Uncategorized

3.4 Quadratic Inequalities (Part 2)

Posted on by

(C) Linear Inequality

Example 1:

  1. Given x = 6 − y 3 find the range of values of x for which y > 9.
  2. Given 2x + 3y – 6 =0, find the range of values of x for which y < 4.

Solution:

(D) Quadratic Inequality

Example 2:

Find the range of values of x which satisfy the following inequalities:

  1. (2x + 1) (3x – 1) < 14
  2. (x – 2) (5x – 4) + 1 > 0

Solution:

 

 

 

 

Nota Ulangkaji SPM Matematik Tingkatan 4 dan Tingkatan 5

Posted on by

Tingkatan 4

Bab 1 Bentuk Piawai

  1. Angka Bererti
    1. Angka Bererti (Bahagian 1)
    2. Angka Bererti (Bahagian 2)
  2. Bentuk Piawai
    1. Bentuk Piawai (Bahagian 1)
    2. Bentuk Piawai (Bahagian 2)
  3. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)

Bab 2 Ungkapan dan Persamaan Kuadratik

  1. Ungkapan Kuadratik
  2. Pemfaktoran Ungkapan Kuadratik
  3. Persamaan Kuadratik
  4. Punca Persamaan Kuadratik
  5. Soalan Model SPM
    1. Soalan Panjang (Kertas 2)


Bab 3 Set

  1. Set
  2. Subset, Set Semesta, dan Set Pelengkap
    1. Subset
    2. Set Semesta
    3. Set Pelengkap
  3. Operasi ke atas Set
    1. Persilangan Set
    2. Kesatuan Set
  4. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)


Bab 4 Penaakulan Matematik

  1. Pernyataan
  2. Pengkuantiti 'Semua' dan 'Sebilangan'
  3. Operasi ke atas Pernyataan
  4. Implikasi
  5. Hujah
  6. Deduksi dan Aruhan
  7. Soalan Model SPM
    1. Soalan Panjang (Kertas 2)

Bab 5 Garis Lurus

  1. Kecerunan Garis Lurus
  2. Kecerunan Garis Lurus dalam Sistem Koordinat Cartesan
  3. Pintasan
  4. Persamaan Garis Lurus
  5. Garis Selari
  6. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)


Bab 6 Statistik III

  1. Selang Kelas
  2. Mod dan Min bagi Data Terkumpul
  3. Histogram Selang Kelas Sama Saiz
  4. Poligon Kekerapan
  5. Kekerapan Longgokan
  6. Sukatan Serakan
  7. Soalan Model SPM
    1. Soalan Panjang (Kertas 2)


Bab 7 Kebarangkalian I

  1. Ruang Sampel
  2. Peristiwa
  3. Kebarangkalian suatu Peristiwa
  4. Soalan Model SPM
    1. Soalan pendek (Kertas 1)

Bab 8 Bulatan III

  1. Tangen kepada Bulatan
  2. Sudut di antara Tangen dengan Perentas
  3. Tangen Sepunya
  4. Soalan Model SPM
    1. Soalan pendek (Kertas 1)


Bab 9 Trigonometri II

  1. Nilai Sin θ, Kos θ, dan Tan θ (0o ≤ θ ≤ 360o)
    1. Bahagian 1
    2. Bahagian 2
  2. Graf Sinus, Kosinus, dan Tangen
  3. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)


Bab 10 Sudut Dongakan dan Sudut Tunduk

  1. Sudut Dongakan dan Sudut Tunduk
  2. Menyelesaikan Masalah yang Melibatkan Sudut Dongakan dan Sudut Tunduk
  3. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)


Bab 11 Garis dan Satah dalam Tiga Dimensi


  1. Sudut di antara Garis dengan Satah
  2. Sudut di antara Dua Satah

Tingkatan 5

Bab 1 Asas Nombor

  1. Nombor dalam Asas Dua, Asas Lapan, dan Asas Lima
    1. Bahagian 1
    2. Bahagian 2
    3. Bahagian 3
    4. Bahagian 4
  2. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)


Bab 2 Garf Fungsi II

  1. Graf bagi beberapa Fungsi (Bahagian 1)
  2. Graf bagi beberapa Fungsi (Bahagian 2)
  3. Penyelesaian Persamaan dengan Kaedah Graf
  4. Rantau Ketaksamaan dalam Dua Pemboleh Ubah
  5. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)


Bab 3 Penjelmaan

  1. Gabungan Dua Penjelmaan
    1. Menentukan Imej suatu Objek bagi Gabungan dua Penjelmaan Isometri
    2. Menentukan Imej suatu Objek bagi Gabungan Penjelmaan yang Melibatkan (a) Dua Pembesaran, (b) Satu Pembesaran dengan Satu daripada Penjelmaan Isometri
    3. Menyatakan Koordinat-koordinat Imej bagi suatu Titik di bawah Gabungan Dua Penjelmaan
    4. Menghuraikan Gabungan Dua Penjelmaan
  2. Menyelesaikan Masalah yang Melibatkan Penjelmaan
  3. Soalan Model SPM
    1. Soalan Panjang (Kertas 2)


Bab 4 Matriks

  1. Matriks
  2. Matriks Sama
  3. Penambahan dan Penolakan
  4. Pendaraban Matriks dengan Nombor
  5. Pendaraban Dua Matriks
  6. Matriks Identiti
  7. Matriks Songsang
  8. Penyelesaian Persamaan Linear Serentak dengan Kaedah Matriks
  9. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)


Bab 5 Ubahan

  1. Ubahan Langsung
    1. Ubahan Langsung (Bahagian 1)
    2. Ubahan Langsung (Bahagian 2)
  2. Ubahan Songsang
  3. Ubahan Tercantum
  4. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)


Bab 6 Kecerunan dan Luas di bawah Graf

  1. Kuantiti yang diwakili oleh Kecerunan Graf
    1. Graf Jarak-Masa
    2. Graf Laju-Masa
  2. Kuantiti yang diwakili oleh Luas di Bawah Graf
  3. Soalan Model SPM
    1. Soalan Panjang (Kertas 2)


Bab 7 Kebarangkalian II

  1. Kebarangkalian Suatu Peristiwa
  2. Kebarangkalian Peristiwa Pelengkap
  3. Kebarangkalian Peristiwa Bergabung
    1. Mencari Kebarangkalian Secara Menyenaraikan Kesudahan Peristiwa Bergabung
    2. Mencari Kebarangkalian Peristiwa Bergabung yang Melibatkan (a) A atau B (b) A dan B
  4. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)


Bab 8 Bearing

  1. Bearing


Bab 9 Bumi sebagai Sfera

  1. Longitud
  2. Latitud
  3. Kedudukan Tempat
  4. Jarak pada Permukaan Bumi
    1. Jarak di antara dua titik diukur sepanjang bulatan agung
    2. Jarak di antara dua titik pada selarian latitud yang sama
    3. Jarak terpendek di antara dua titik 
  5. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)


Bab 10 Pelan dan Dongakan

  1. Unjuran Ortogon
  2. Pelan dan Dongakan
  3. Soalan Model SPM
    1. Soalan Panjang (Kertas 2)


Nota Ulangkaji SPM Matematik Tambahan Tingkatan 4 dan Tingkatan 5

Posted on by

Tingkatan 4

Bab 1 Fungsi

  1. Hubungan
    1. Domain dan Kodomain
    2. Jenis Hubungan
  2. Fungsi
    1. Fungsi Sebagai Sejenis Hubungan Khas dan Tatatanda Fungsi 
    2. Domain, Kodomain, Objek, Imej dan Julat bagi Suatu Fungsi serta Fungsi Nilai Mutlak
  3. Fungsi Gubahan
    1. Cara Perbandingan
    2. Cari Fungsi Baru dengan Menggunakan Fungsi Gubahan yang diberi
  4. Fungsi Songsangan
  5. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)

Bab 2 Persamaan Kuadratik



Bab 3 Fungsi Kuadratik



Bab 4 Persamaan Serentak



Bab 5 Indeks dan Logaritma



Bab 6 Geometri Koordinat


Bab 7 Statistik

  1. Sukatan Kecenderungan Memusat
    1. Min
    2. Mod
    3. Median
  2. Sukatan Serakan
    1. Julat
    2. Julat antara Kuartil (Bahagian 1)
    3. Julat antara Kuartil (Bahagian 2)
    4. Varians dan Sisihan Piawai
  3. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)

Bab 8 Sukatan Membulat



Bab 9 Pembezaan



Bab 10 Penyelesaian Segitiga

  1. Petua Sinus
  2. Petua Kosinus
  3. Luas Segitiga
  4. Soalan Model SPM
    1. Soalan Panjang (Kertas 2)

Bab 11 Nombor Indeks

  1. Nombor Indeks
  2. Indeks Gubahan
  3. Soalan Model SPM
    1. Soalan Panjang (Kertas 2)


Tingkatan 5

Bab 1 Janjang

  1. Janjang Aritmetik
    1. Mengenal pasti Janjang Aritmetik
    2. Menentukan Sebutan Tertentu dan Bilangan Sebutan dalam suatu Janjang Aritmetik
    3. Hasil Tambah Janjang Aritmetik
  2. Janjang Geometri
    1. Mengenal pasti Janjang Geometri
    2. Menentukan Sebutan Tertentu dan Bilangan Sebutan dalam suatu Janjang Geometri
    3. Hasil Tambah Janjang Geometri
    4. Hasil Tambah Janjang Geometri Sehingga Ketakterhinggaan
  3. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)

Bab 2 Hukum Linear



Bab 3 Pengamiran



Bab 4 Vektor



Bab 5 Fungsi Trigonometri

  1. Sudut Positif dan Sudut Negatif dalam Darjah dan Radian
  2. Enam Fungsi Trigonometri bagi Sebarang Sudut
    1. Mentakrifkan sinus, kosinus, tan, kosek, sek dan kot
    2. Sudut Khas
  3. Graf Fungsi Sinus, Kosinus dan Tangen
    1. Graf Fungsi Sinus, Kosinus dan Tangen
    2. Melakar Graf Fungsi Trigonometri (Bahagian 1)
    3. Melakar Graf Fungsi Trigonometri (Bahagian 2)
  4. Identiti Asas
  5. Rumus bagi Sin (A ± B), Kos (A ± B), Tan (A ± B), Sin 2A, Kos 2A dan Tan 2A
  6. Menyelesaikan Persamaan Trigonometri Mudah
    1. Persamaan asas dalam sin x/ kos x/ tan x/ kosek x/ sek x/ kot x
    2. Pemfaktoran
    3. Bentuk Persamaan Kuadratik dalam sin x/ kos x/ tan x/ kosek x/ sek x/ kot x
    4. Melibatkan Rumus penambahan dan Rumus bagi Sudut Berganda)
  7. Soalan Model SPM
    1. Soalan Pendek (Kertas 1)
    2. Soalan Panjang (Kertas 2)

Bab 6 Pilir Atur dan Gabungan



Bab 7 Kebarangkalian Mudah



Bab 8 Taburan Kebarangkalian




Derive By First Principle – Example 1

Posted on by

Solving Equation of Index Number

Example

Derive the equation $$y = {x^2} + \frac{3}{x}$$ by using first principle.

$$\eqalign{ & y = {x^2} + \frac{3}{x} \cr & \frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\delta x \to 0} \frac{{\delta y}}{{\delta x}} \cr & = \mathop {\lim }\limits_{\delta x \to 0} \frac{{\left( {y + \delta y} \right) – y}}{{\delta x}} \cr & = \mathop {\lim }\limits_{\delta x \to 0} \frac{{\left[ {{{\left( {x + \delta x} \right)}^2} + \frac{3}{{x + \delta x}}} \right] – \left[ {{x^2} + \frac{3}{x}} \right]}}{{\delta x}} \cr & = \mathop {\lim }\limits_{\delta x \to 0} \frac{{{x^2} + 2x\delta x + \delta {x^2} – {x^2} + \frac{3}{{x + \delta x}} – \frac{3}{x}}}{{\delta x}} \cr & = \mathop {\lim }\limits_{\delta x \to 0} \frac{{2x\delta x + \delta {x^2}}}{{\delta x}} + \frac{{\frac{{3x – 3(x + \delta x)}}{{x(x + \delta x)}}}}{{\delta x}} \cr & = \mathop {\lim }\limits_{\delta x \to 0} 2x + \delta x + \frac{{ -3 \delta x}}{{x(x + \delta x)}} \times \frac{1}{{\delta x}} \cr & = \mathop {\lim }\limits_{\delta x \to 0} 2x + \delta x + \frac{{ – 3}}{{x(x + \delta x)}} \cr & = 2x – \frac{3}{{{x^2}}} \cr} $$

$$\frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\delta x \to 0} \frac{{\delta y}}{{\delta x}}$$

4.4 Lipids

Posted on by
[adinserter block="3"]
  1. Lipids are complex organic compounds that made up of carbon, hydrogen and oxygen. Some lipids contain the elements nitrogen and phosphorus.
  2. The ratio of hydrogen atoms to oxygen atoms in a lipid molecule is higher than the    2 : 1 ratio in carbohydrates.
  3. Lipids are insoluble in water. However, they are soluble in other lipids and organic solvents such as alcohol and acetone.
  4. The basic units of lipids are fatty acids and glycerol. A lipid molecule is made up of one molecule of glycerol and three molecules of fatty acid.


(Formation of molecule of lipid)

[adinserter block="3"]
Types of Lipids
  1. Examples of lipids include
    1. fats and oils (triglycerides), 
    2. waxes, 
    3. phospholipids
    4. steroids.
  2. Fats and oils (triglycerides)
    1. A triglyceride is formed from glycerol and three molecules of fatty acids through condensation.
    2. Triglycerides can be broken down into fatty acids and glycerol by hydrolysis.
    3. There are two types of fats.
      1. Saturated fats
        1. Fats containing saturated fatty acids
        2. are solids at room temperature.
      2. Unsaturated fats
        1. Fats containing unsaturated fatty acids
        2. usually Iiquid at room temperature
        3. it is called oil 
  3. Waxes
    1. Waxes are long chain esters.
    2. They are found in the cuticle of leaves.
    3. They are waterproof
    4. They can prevents entry of microorganisms and evaporation of water
  4. Phospholipids
    1. Phospholipids are component of plasma membrane.
    2. Example of phospholipid is lecithin. It is a type of triglyceride, which is the main constituent of the plasma membrane.
  5. Steroids
    1. Steroids include cholesterol and hormones such as testosterone, oestrogen and progesterone.
    2. Steroids have a basic structure which consists of four interconnected rings of carbon atoms. Attached to this basic structure are side chains of different lengths.
[adinserter block="3"]

4.3 Protein

Posted on by
[adinserter block="3"]
  1. Proteins are complex compounds that made up of carbon, hydrogen and nitrogen. Some proteins contain sulphur and phosphorus.
  2. It is needed by the body for 
    1. growth, 
    2. repair of damaged tissues and 
    3. synthesis of secretions (enzymes, mucus, hormones.)
  3. Proteins are polymer that made up of monomers called amino acids. Each molecule of amino acid has one amino group (-NH2) and one carboxyl group ( -COOH).
  4. Two molecules of amino acids are joined by a peptide bond to form a dipeptide through condensation.
    Amino acid + amino acid → dipeptide + water
  5. Polypeptides (protein) are formed when many amino acids are joined together by condensation.
  6. Proteins can be broken down through hydrolysis into amino acids.
  7. There are 20 types of amino acids in cells.
  8. Amino acid can be divided into essential amino acid and nonessential amino acid.
    1. Essential amino acids are amino acids that cannot be synthesised by the body. They can only be obtained from diets. An example is leucine.
    2. Non-essential amino acids are amino acids that can be synthesised by the body. They are derived from other amino acids. There are 11 non-essential amino acids.
  9. Proteins can be grouped into four levels of organisation according to their structures.
    1. Primary structure (linear sequence of amino acids in a polypeptide.)
    2. Secondary structure (polypeptide is coiled to form an alpha-helix or folded into beta-pleated sheets)
    3. Tertiary structure (helix or beta-pleated sheets are folded in many ways into a three dimensional shape of a polypeptide.)
    4. Examples are hormones, enzymes, antibodies and plasma proteins.
    5. Quarternary structure (Two or more tertiary structure polypeptide chains combine to form a large and complex protein molecule. Example: haemoglobin.)



[adinserter block="3"]

4.2.3 Polysaccharides

Posted on by
[adinserter block="3"]
  1. Polysaccharides are formed when more than two monosaccharides (usually more than hendreds) combine through condensation. 
  2. Some characteristics of polysacharides are: 
    1. do not dissolve in water 
    2. do not taste sweet 
    3. do not crystallise
  3. Polysaccharides can be hydrolysed by adding acid, boiling and action of enzymes. 
  4. Examples of polysaccharides 
    1. Starch
      storage of carbohydrate in plants. The iodine test is used for confirming the presence of starch
    2. Glycogen
      storage of carbohydrate in animals. Its polysaccharide chains are branched
    3. Cellulose
      structural polysaccharide in plant cells. They are the constituent of the cell walls of plant cells and chitin of animal cuticles. Gives support to plant cells.
  5. Polysaccharides can be broken down into smaller molecules through hydrolysis using dilute acid or enzymes.
[adinserter block="3"]

SPM Form 5 Biology – Exercises

Posted on by

01 Transport 

  1. The Circulatory System (7 Questions) 
  2. The Mechanism of Blood Clotting (3 Questions) 
  3. The Lymphatic System (4 Questions) 
  4. The Role of Circulatory System in Body Defense Mechanism (4 Questions) 

02 Support and Locomotion 

  1. Support and Locomotion in Humans and Animals 1 (6 Questions) 
  2. Support and Locomotion in Humans and Animals 2 (6 Questions) 
  3. Support System in Plants (4 Questions) 

03 Coordination and Response 

  1. The Role of the Human Nervous System 1 (6 Questions) 
  2. The Role of the Human Nervous System 2 (6 Questions) 
  3. The Role of Hormones in Humans (7 Questions) 
  4. Homeostasis in Humans (7 Questions) 

04 Reproduction and Growth 

  1. Formation of Gamete (5 Questions) 
  2. Roles of Hormones in the Menstrual Cycle (5 Questions) 

05 Inheritance (10 Questions) 


06 Variation (9 Questions)