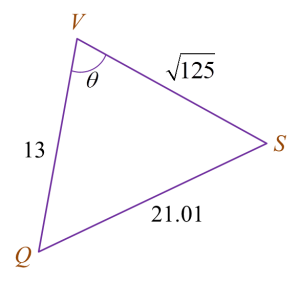
Soalan 7 (2 markah):
Diberi bahawa sebutan ke-n bagi suatu janjang geometri ialah
Nyatakan
(a) nilai k,
(b) sebutan pertama bagi janjang itu.
Penyelesaian:
(a)
k = 0, k = 1 atau k = -1 (salah satu daripada jawapan ini).
(b)
Diberi bahawa sebutan ke-n bagi suatu janjang geometri ialah
Nyatakan
(a) nilai k,
(b) sebutan pertama bagi janjang itu.
Penyelesaian:
(a)
k = 0, k = 1 atau k = -1 (salah satu daripada jawapan ini).
(b)
Soalan 8 (3 markah):
Diberi bahawa hasil tambah n sebutan pertama bagi suatu janjang aritmetik ialah
Cari sebutan ke-n.
Penyelesaian:
Diberi bahawa hasil tambah n sebutan pertama bagi suatu janjang aritmetik ialah
Cari sebutan ke-n.
Penyelesaian:
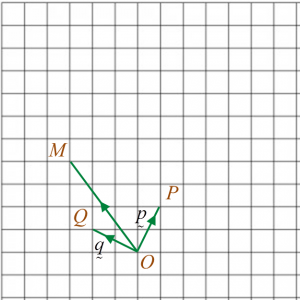 Rajah
Rajah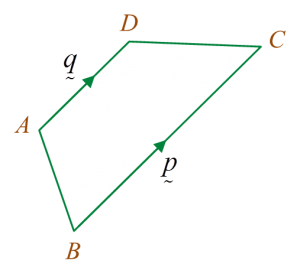 Rajah
Rajah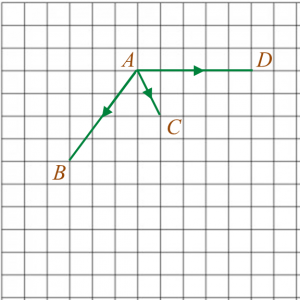 Rajah
Rajah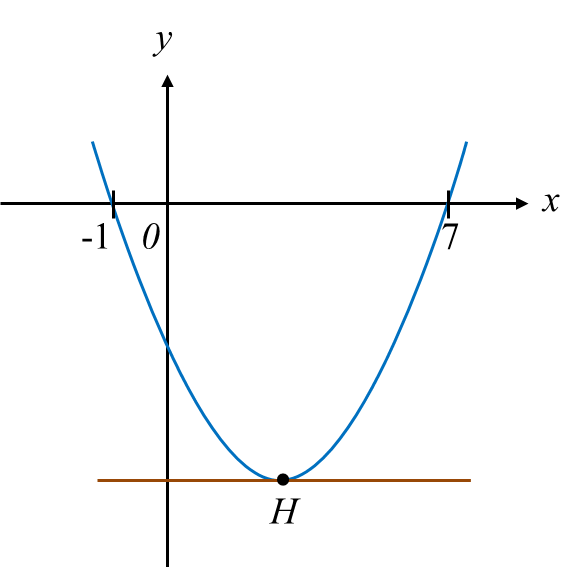 Rajah
Rajah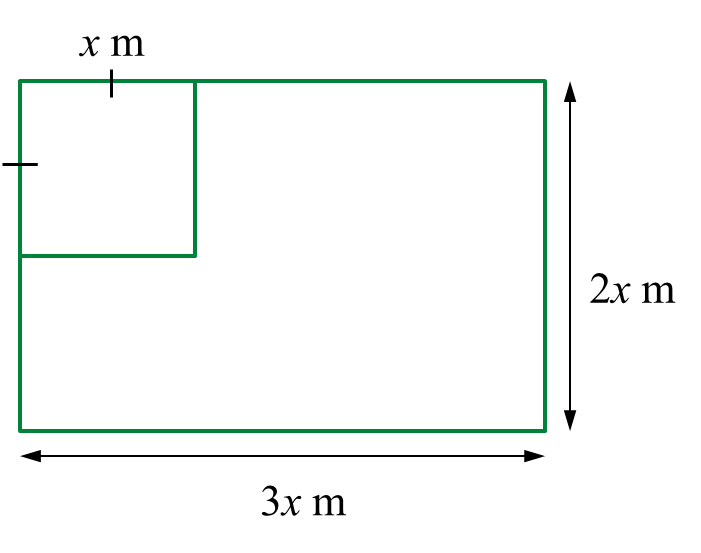
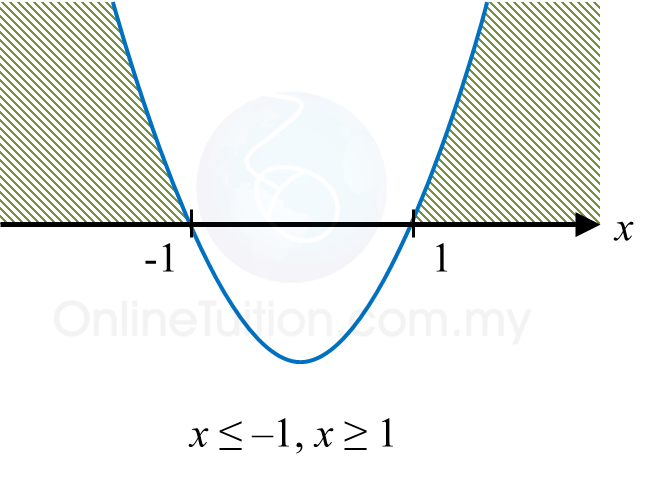
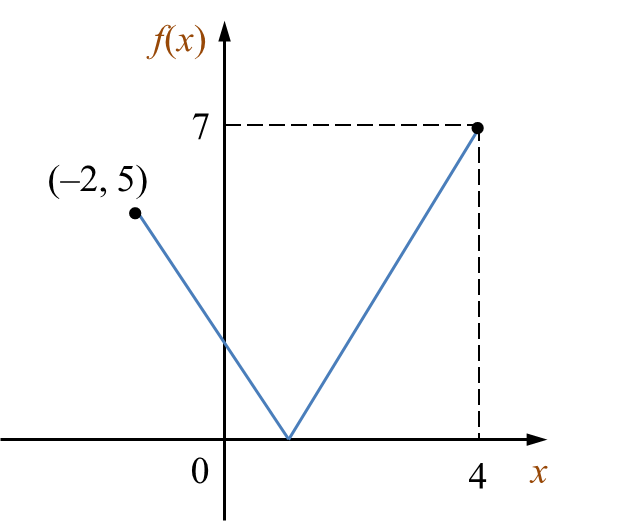 Rajah
Rajah 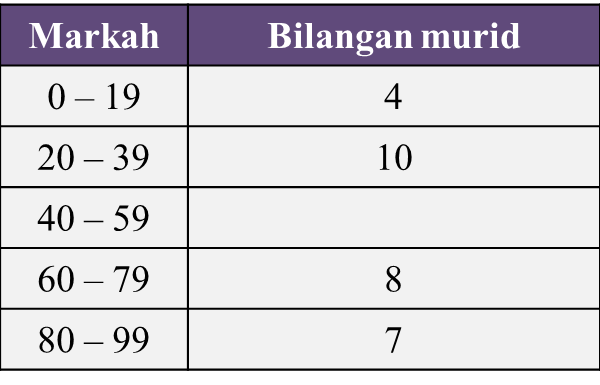 Jadual
Jadual