Question 2:
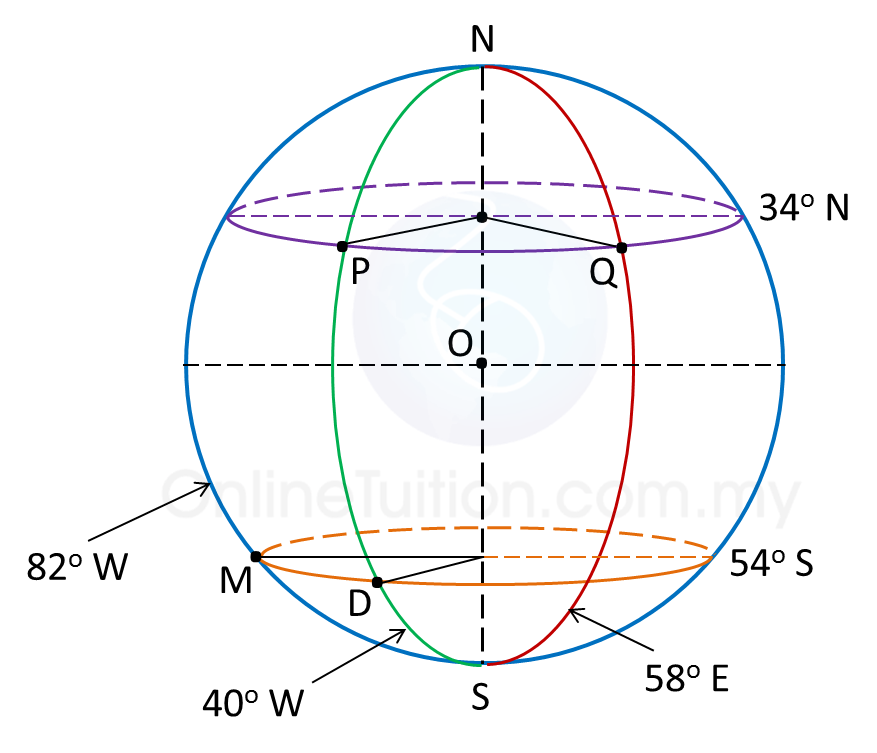
P(25o S, 40o E), Q(θo N, 40o E), R(25o S, 10o W) and K are four points on the surface of the earth. PK is the diameter of the earth.
(a) State the location of point K.
(b) Q is 2220 nautical miles from P, measured along the same meridian.
Calculate the value of θ.
(c) Calculate the distance, in nautical mile, from P due west to R, measured along the common parallel of latitude.
(d) An aeroplane took off from Q and flew due south to P. Then, it flew due west to R. The average speed of the aeroplane was 600 knots.
Calculate the total time, in hours, taken for the whole flight.
Solution:

(a)
As PK is the diameter of the earth, therefore latitude of K = 25o N
Longitude of K= (180o – 40o) W = 140o W
Therefore, location of K = (25o N, 140oW).
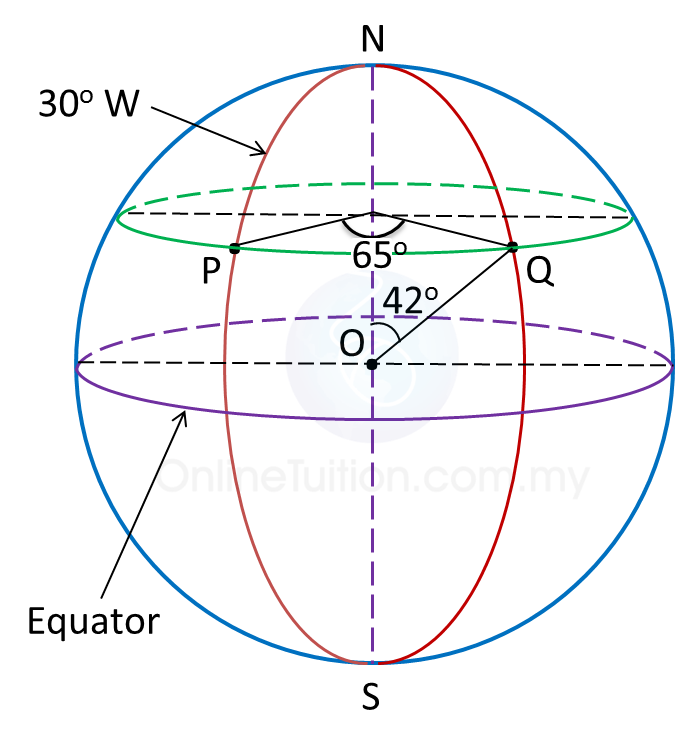
(b)
Let the centre of the earth be O.
∠POQ=222060=37oθo=37o−25o=12o∴The value ofθis 12.
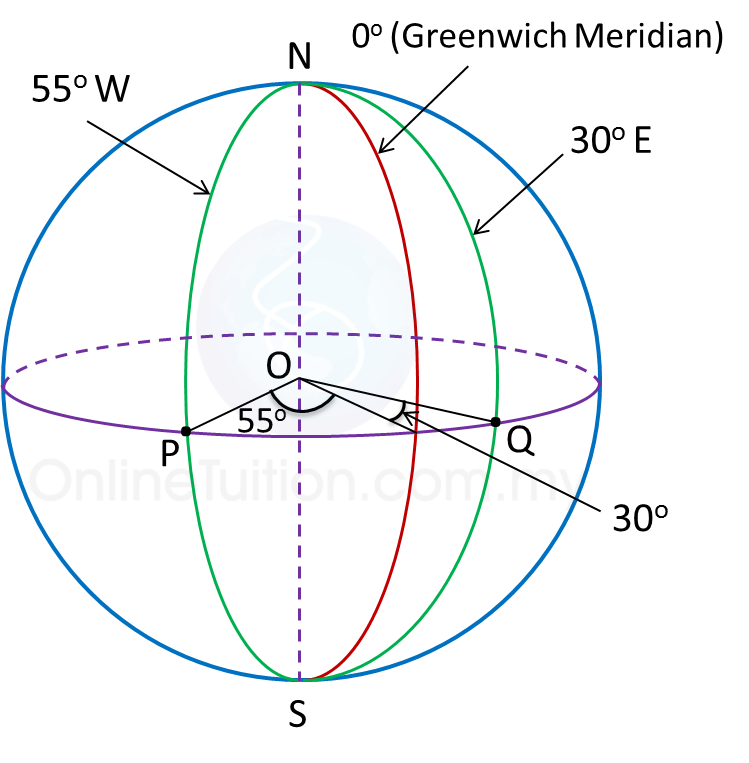
(c)
Distance from P to R
= (40 + 10) × 60 × cos 25o
= 50 × 60 × cos 25o
= 2718.92 n.m.
(d)
Total distance travelled
= distance from Q to P + distance from P to R
= 2220 + 2718.92
= 4938.92 nautical miles
Time taken =total distance fromQtoRaverage speed=4938.92600=8.23hours
Time taken =total distance fromQtoRaverage speed=4938.92600=8.23hours