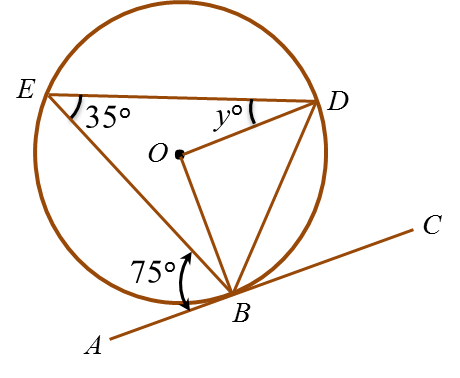
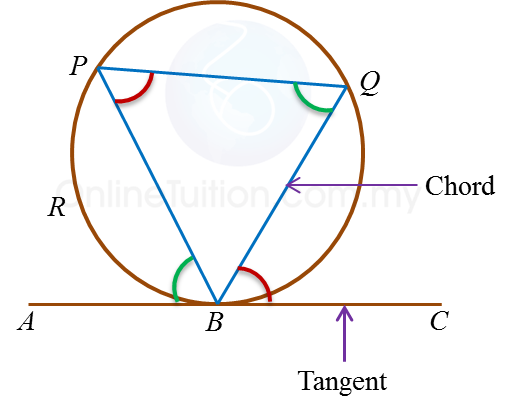
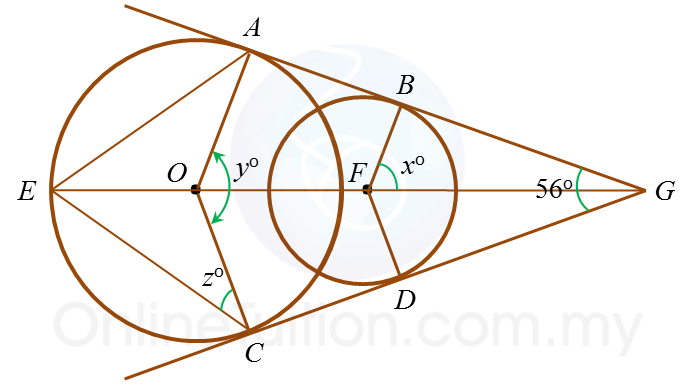
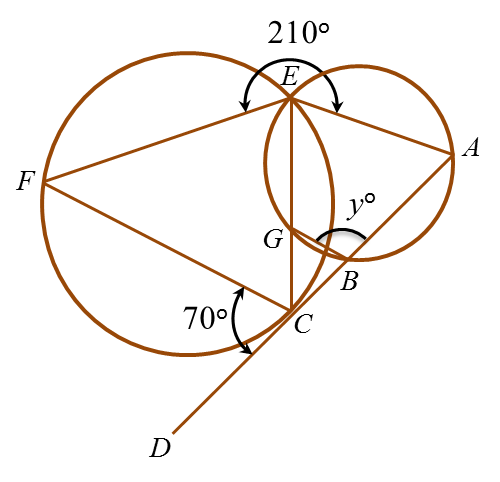
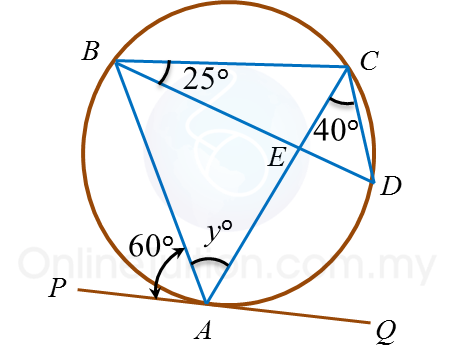
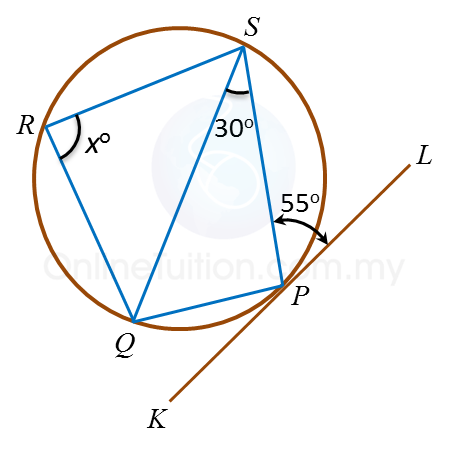
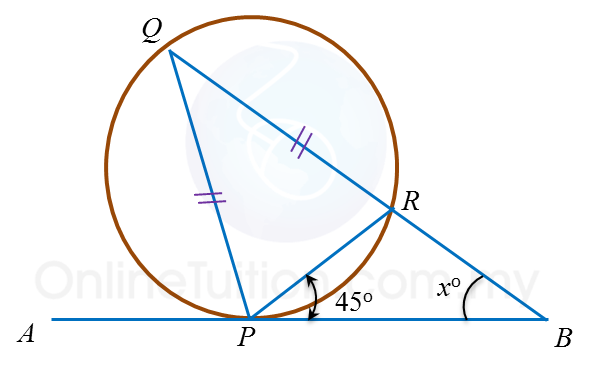
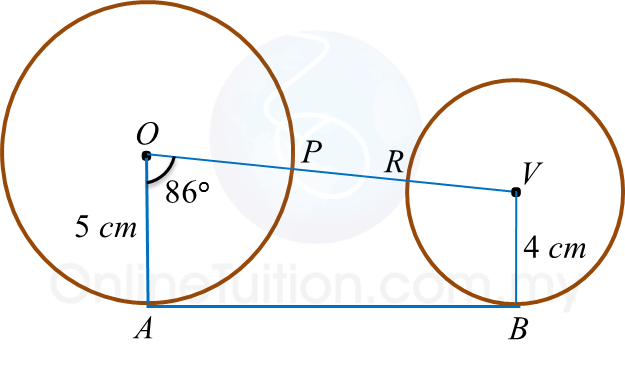
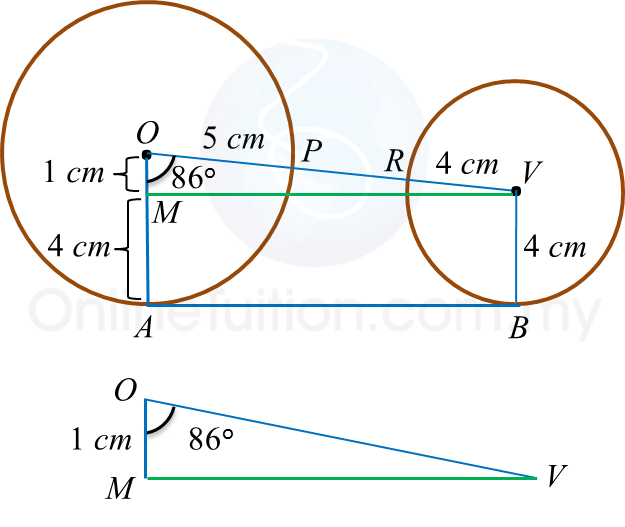
Question 10:
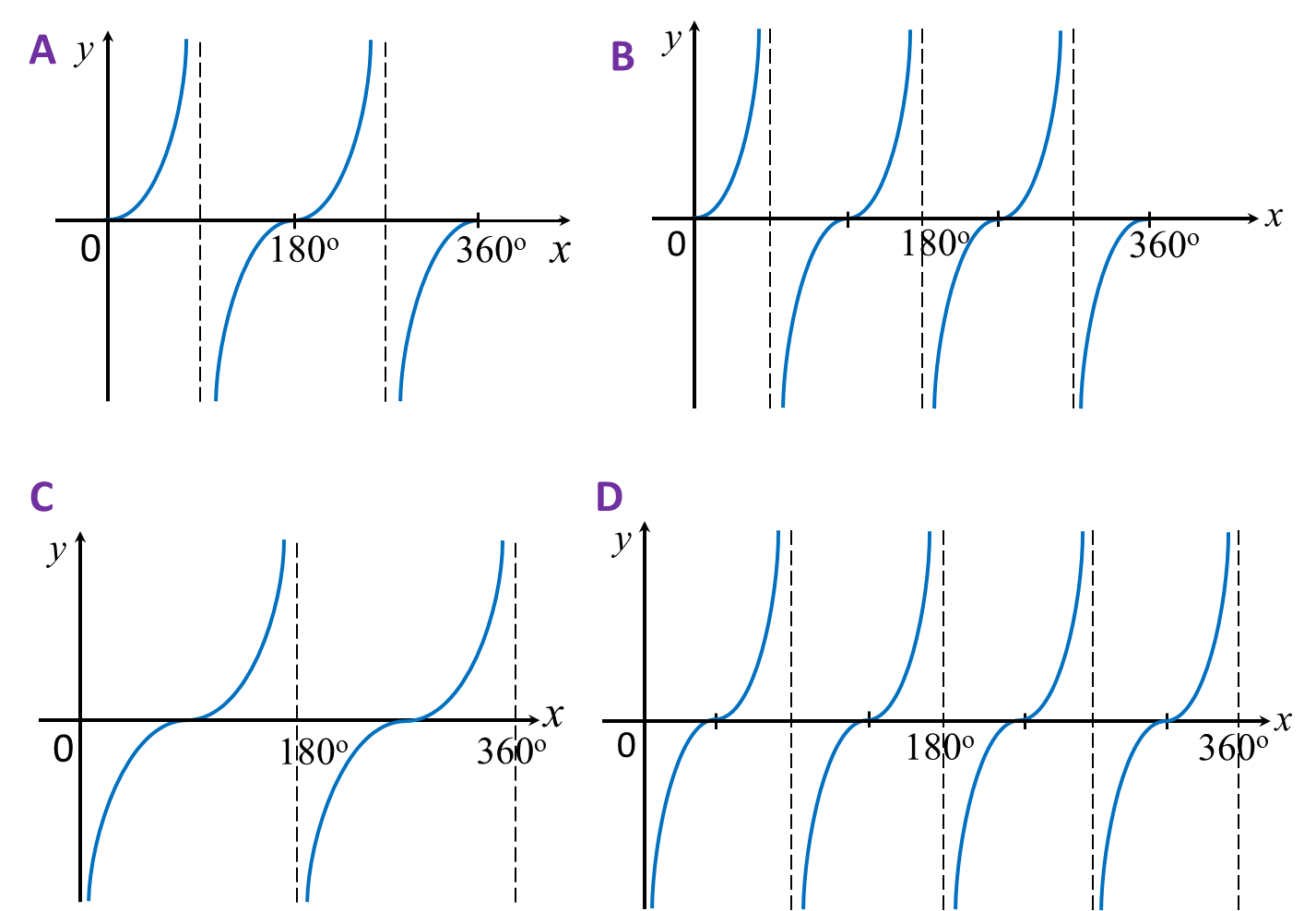
Which of the following graph represents y = cos 2x?
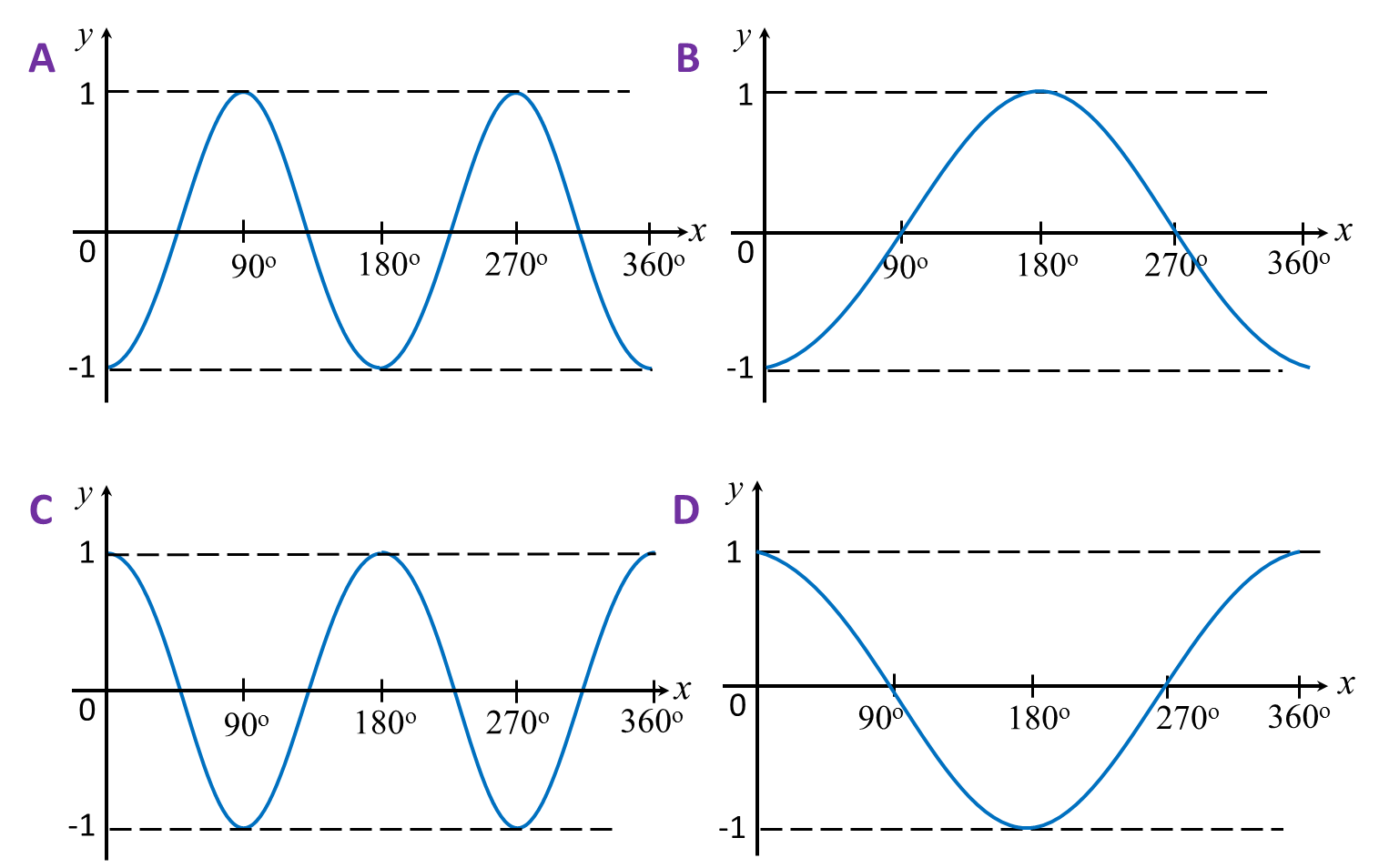
Solution:
Answer: C
Question 11:
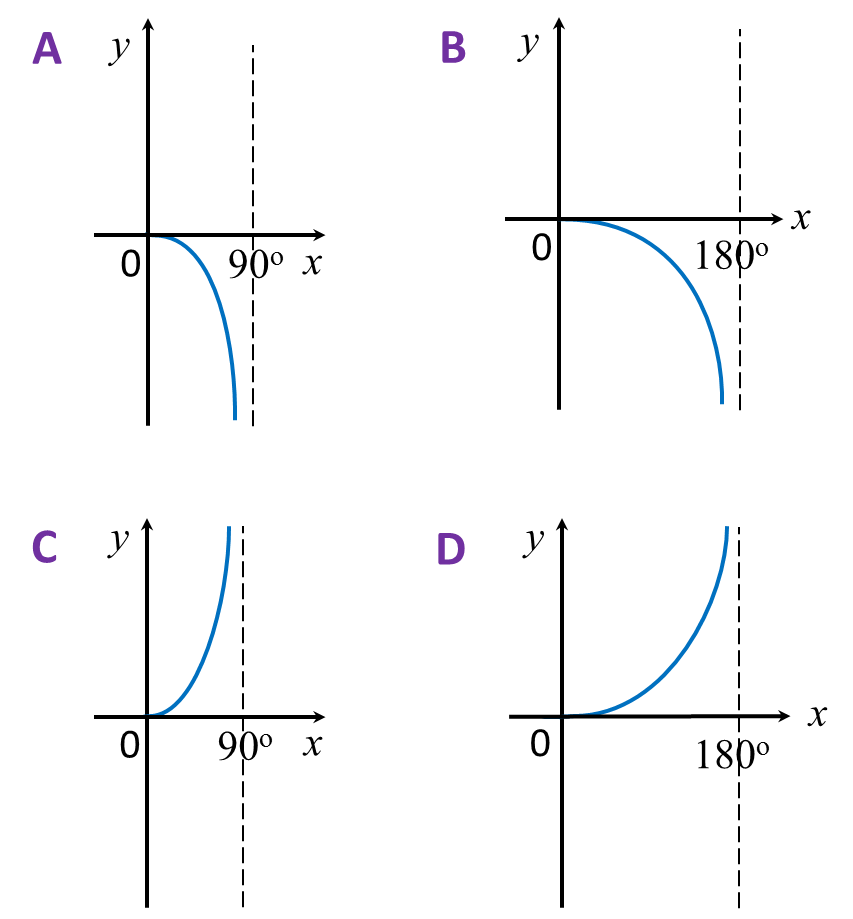
Which of the following graph represents y = cos x for 0o ≤ x ≤ 180o?
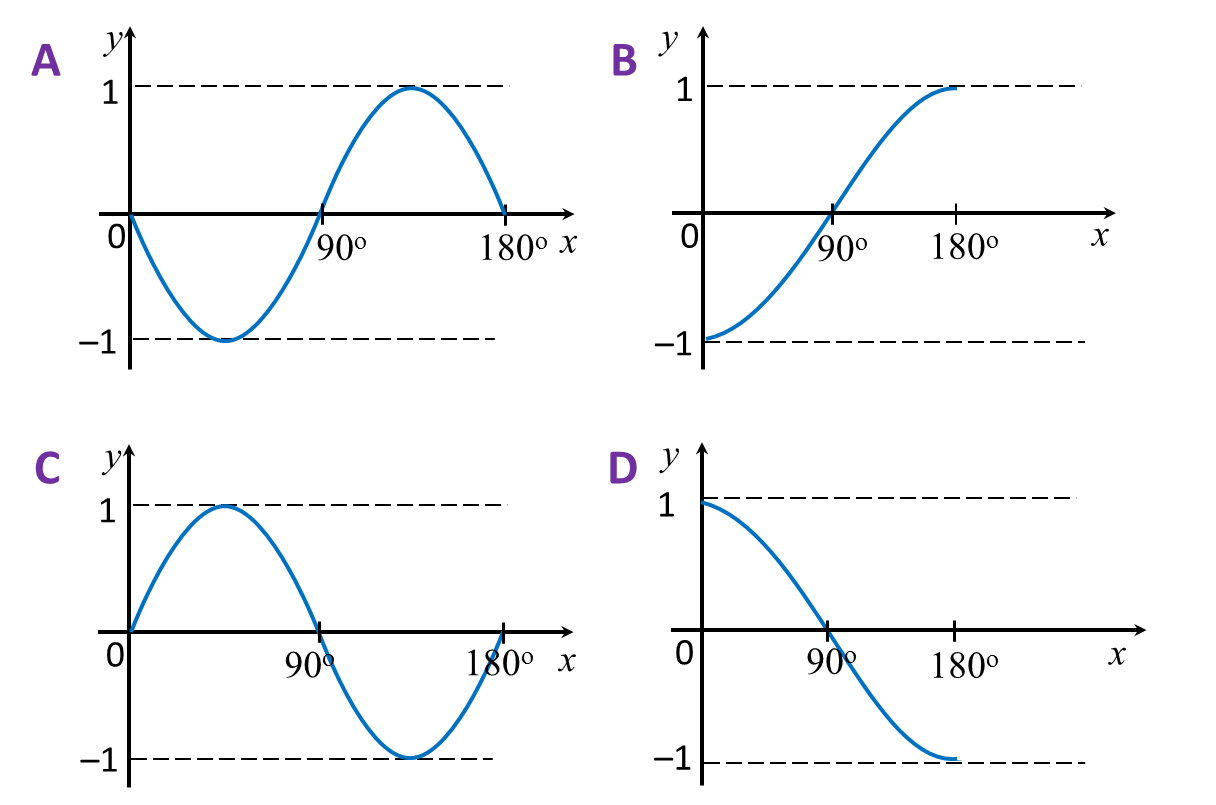
Solution:
Answer: D
Question 12:
Which graph represents part of y = cos x?
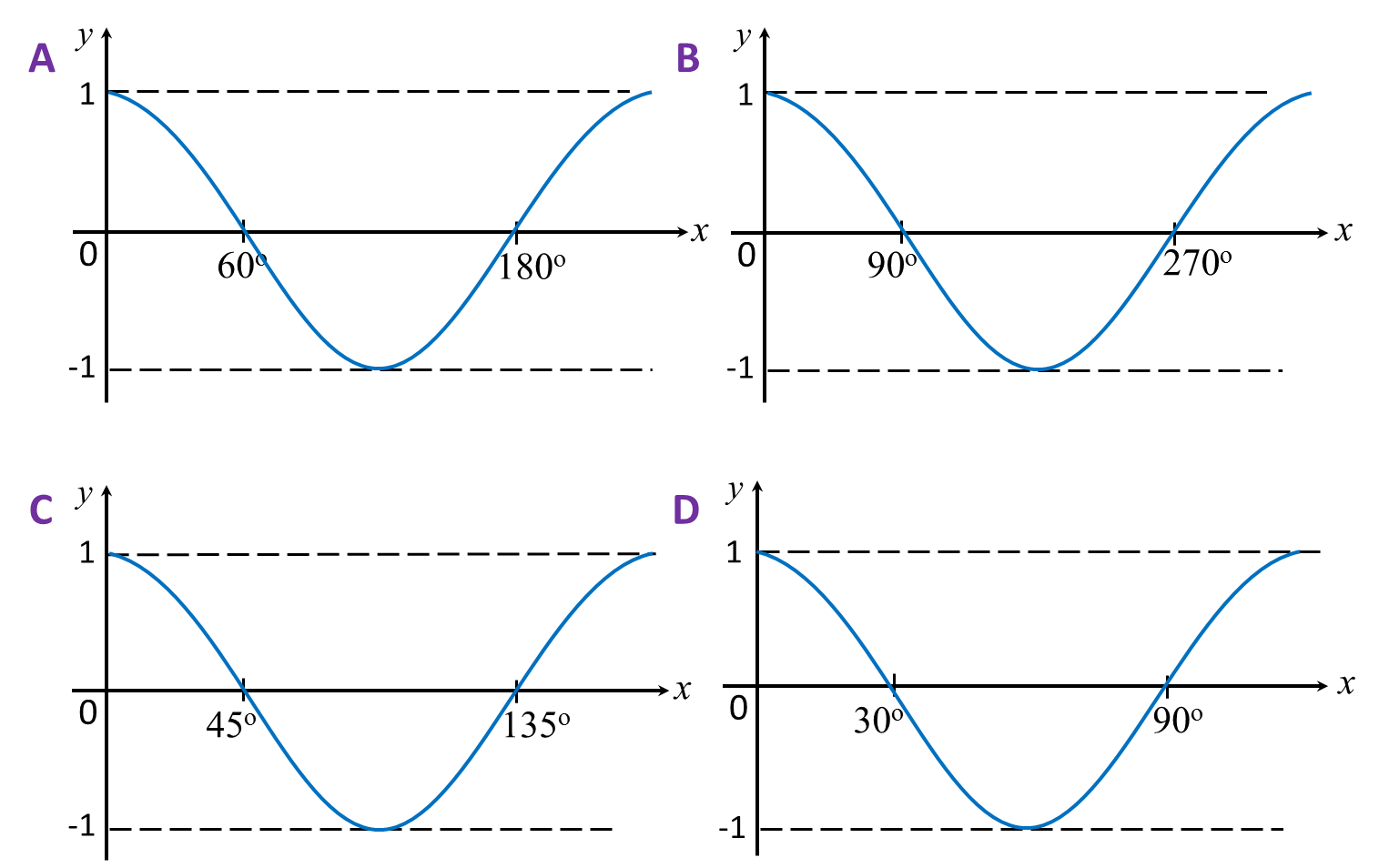
Solution:
Answer: B