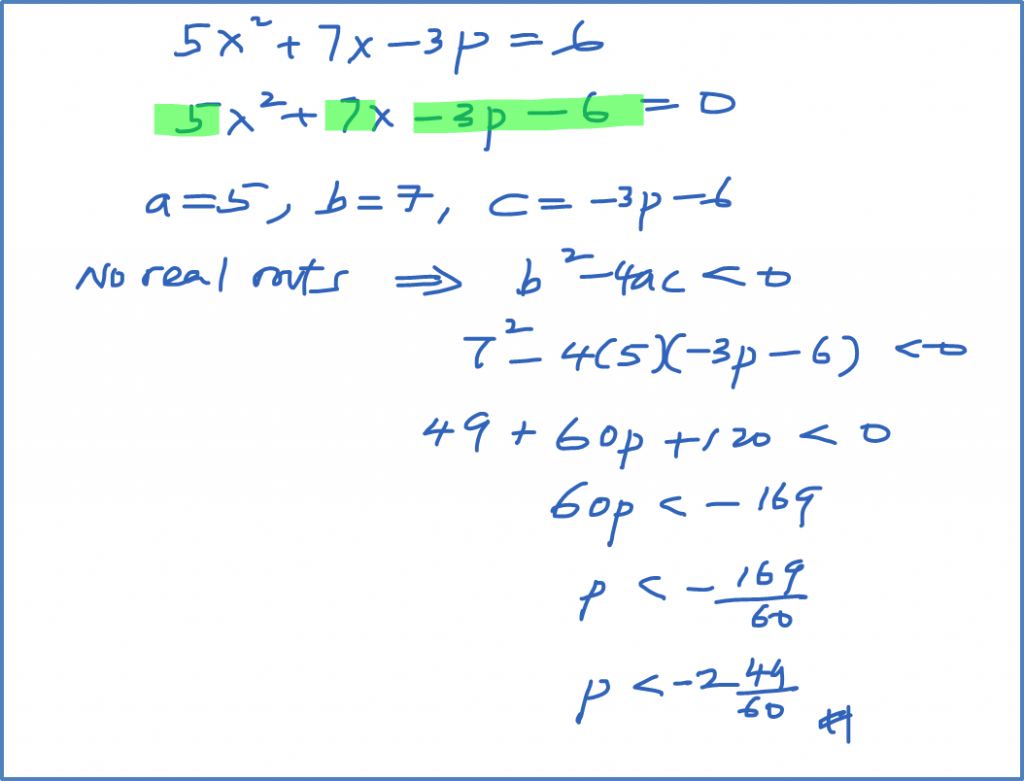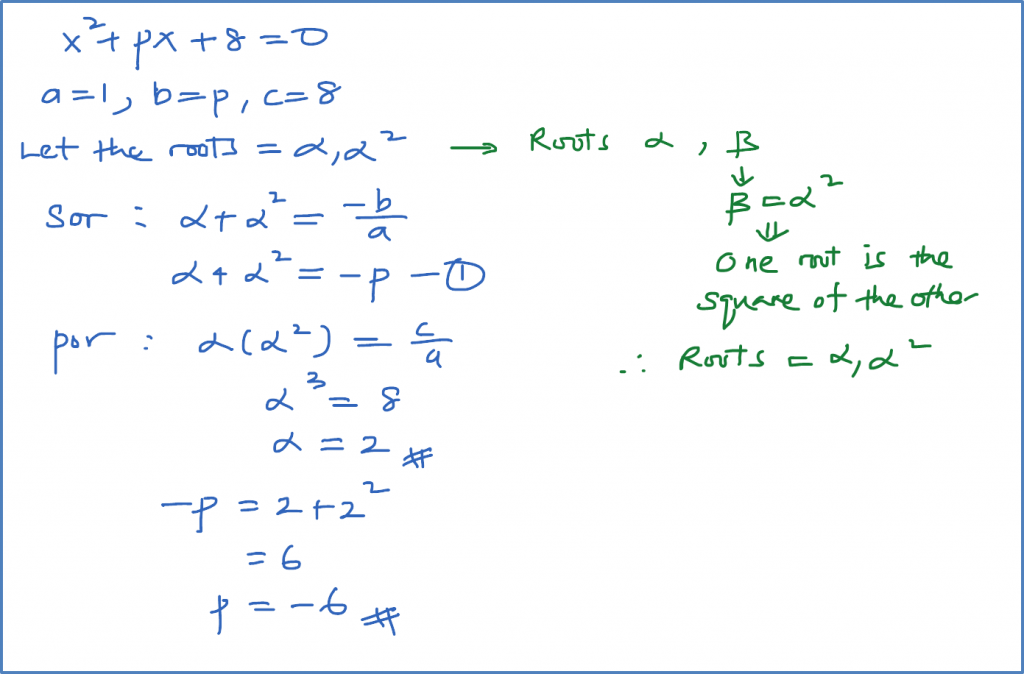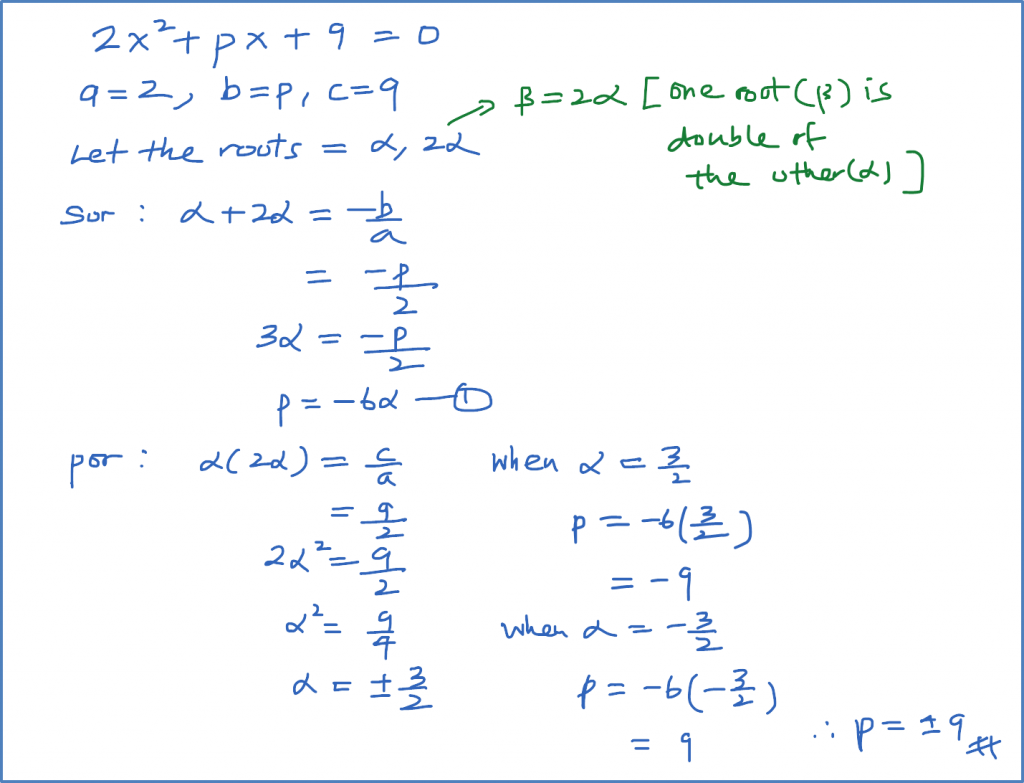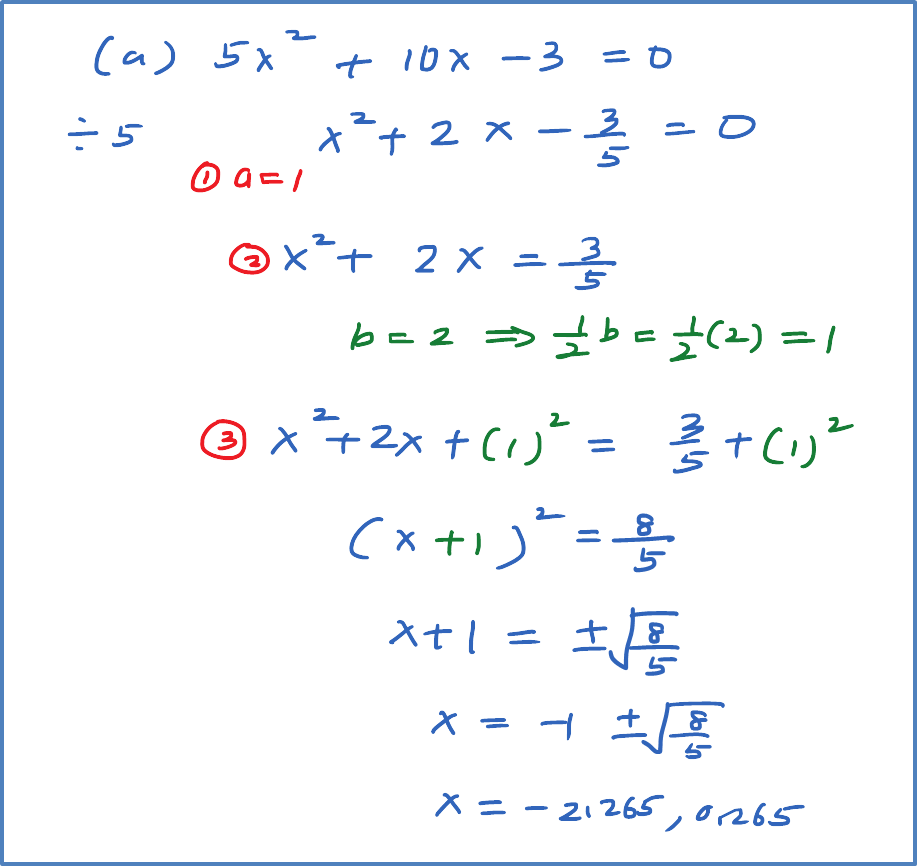3.2a Finding the Maximum/minimum and Axis of Symmetry of a Quadratic Function

Posted on by
Example 1
State the maximum or minimum value of   for each of the following quadratic function and state the value of x at which the function is maximum or minimum.  Find the maximum or minimum point and finally state axis of symmetry for each case.

(a) f(x)=−2(x−3)2+4
(b) f(x)=3(x−4)2+10
(c) f(x)=−3(x+2)2−9
(d) f(x)=−8+2(x+5)2






Correction for part (d) of the question,
when x + 5 = 0, x = -5
minimum point is (-5, -8)
Axis of symmetry, x = -5




3.1 Graph of Quadratic Functions

Posted on by
  1. The graph of quadratic function is parabola.
  2. When the coefficient of x2 is positive the graph is a parabola with ∪ shape.
  3. When the coefficient of x2 is negative the graph is a parabola with ∩ shape.

(A) Axis of Symmetry

The axis of symmetry is a vertical line passing through the maximum or minimum point of the parabola.

 

 

 

(A) General Form of Quadratic Function

Posted on by

3.1 General Form of Quadratic Function
General form of a quadratic function is f(x)=ax2+bx+c where a, b, and c are constants and a ≠ 0, and x as a variable.

Example:
Determine which of the following is a quadratic function.
  1. f(x)=(5x−3)(3x+8)
  2. f(x)=2(3x+8)
  3. f(x)=52x2
Answer:
(a)
  f(x)=(5x−3)(3x+8)f(x)=15x2+40x−9x−24f(x)=15x2+31x−24
Quadratic function

(b)
f(x)=2(3x+8)f(x)=6x+16
Not quadratic function


(c) Not quadratic function

SPM Practice (Paper 1)

Posted on by
Question 11:
The quadratic equation x2−4x−1=2p(x−5) , where p is a constant, has two equal roots. Calculate the possible values of p.

Solution:




Question 12:
Find the range of values of k for which the equation x2−2kx+k2+5k−6=0 has no real roots.

Solution:




Question 13:
Find the range of values of p for which the equation 5x2+7x−3p=6 has no real roots.

Solution:

SPM Practice (Paper 1)

Posted on by
Question 6:
Write and simplify the equation whose roots are the reciprocals of the roots of 3x2+2x−1=0 , without solving the given equation.

Solution:





Question 7:
Find the value of p if one root of x2+px+8=0 is the square of the other.

Solution:





Question 8:
If one root of 2x2+px+9=0 is twice the other, find the values of p.

Solution:


SPM Practice (Paper 1)

Posted on by

Question 1:
Solve the following quadratic equations by factorisation.
(a) x2−5x−10=−4(b) 3−x−2x2=0(c) 11a=2a2+12(d) 2x+73x−2=x

Solution:








Question 2:
Solve the following quadratic equations by completing the square.
(a) 5x2+10x−3=0(b) 2x2−5x−6=0

Solution:





2.4 Discriminant of a Quadratic Equation

Posted on by

The Discriminant

The expression b2−4ac in the general formula is called the discriminant of the equation, as it determines the type of roots that the equation has.



Example
Determine the nature of the roots of the following equations.
a. 5x2−7x+3=0
b. x2−4x+4=0
c. −2x2+5x−9=0

Answer:



2.3d Forming New Quadratic Equation given a Quadratic Equation (Example)

Posted on by
Example

If the roots of x2−3x−7=0   are α  and β  , find the equation whose roots are α2β   and αβ2 .

Solution

Part 1 : Find SoR and PoR for the quadratic equation in the question




Part 2 : Form a new quadratic equation by finding SoR and PoR




Finding the Sum of Roots (SOR) and Product of Roots (POR) of a Quadratic Equation (Example)

Posted on by

Example
The roots of 2x2+3x−1=0   are α and β.  Find the values of
(a) (α+1)(β+1)
(b) 1α+1β
(c) α2β+αβ2
(d) αβ+βα

[Clue: α2+β2=(α+β)2−2αβ   ]






Finding the Sum of Roots (SoR) and Product of Roots (PoR)

Posted on by
2.6 Finding the Sum of Roots (SoR) and Product of Roots (PoR)



Example
Find the sums and products of the roots of the following equations.
a. x2+7x−3=0
b. x(x−1)=5(1−x)

Answer:
(a)
x2+7x−3=0a=1, b=7, c=−3Sum of Rootsα+β=−ba=−71=−7Product of Rootsαβ=ca=−31=−3

(b)
x(x−1)=5(1−x)x2−x=5−5xx2−x+5x−5=0x2+4x−5=0a=1, b=4, c=−5Sum of Rootsα+β=−ba=−41=−4Product of Rootsαβ=ca=−51−5