3.1c Menyatakan Koordinat-koordinat Imej bagi suatu Titik di bawah Gabungan Dua
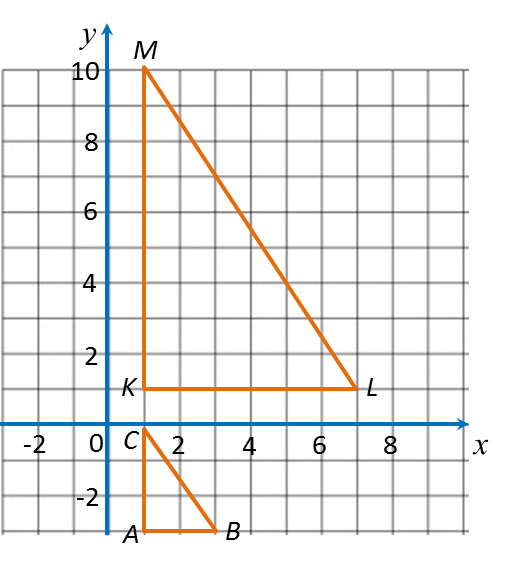
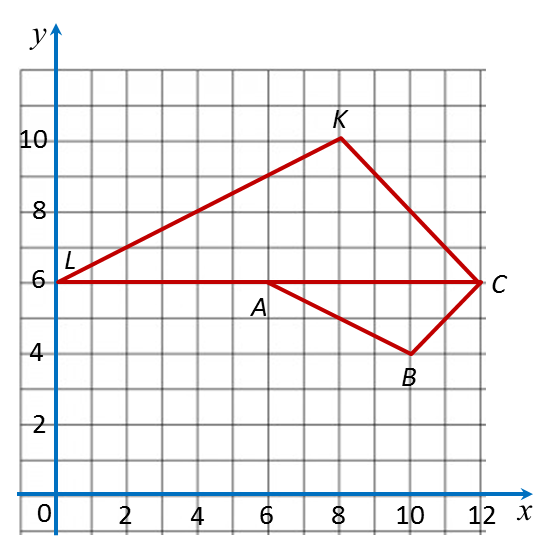
1. Koordinat-koordinat bagi imej satu titik, K, di bawah suatu gabungan penjelmaan AB, boleh ditentukan dengan langkah-langkah berikut:
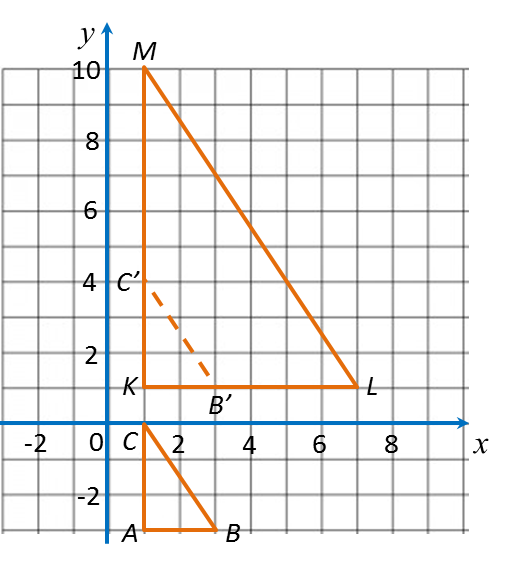
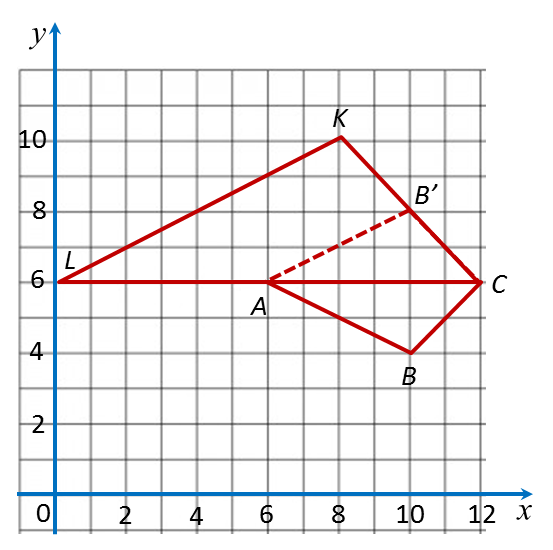
Step 1: Menentukan koordinat-koordinat K’, imej bagi K, di bawah penjelmaan pertama, B.
Step 2: Menentukan koordinat-koordinat K”, imej bagi K’, di bawah penjelmaan kedua, A. K” ialah imej bagi K, di bawah gabungan penjelmaan AB.
Contoh:
T, P, R dan E adalah empat penjelmaan yang ditakrifkan seperti berikut:
P = pantulan pada paksi-y.
R = Putaran 90o ikut arah jam pada asalan.
E = Satu pembesaran pada asalan dengan faktor skala 3.
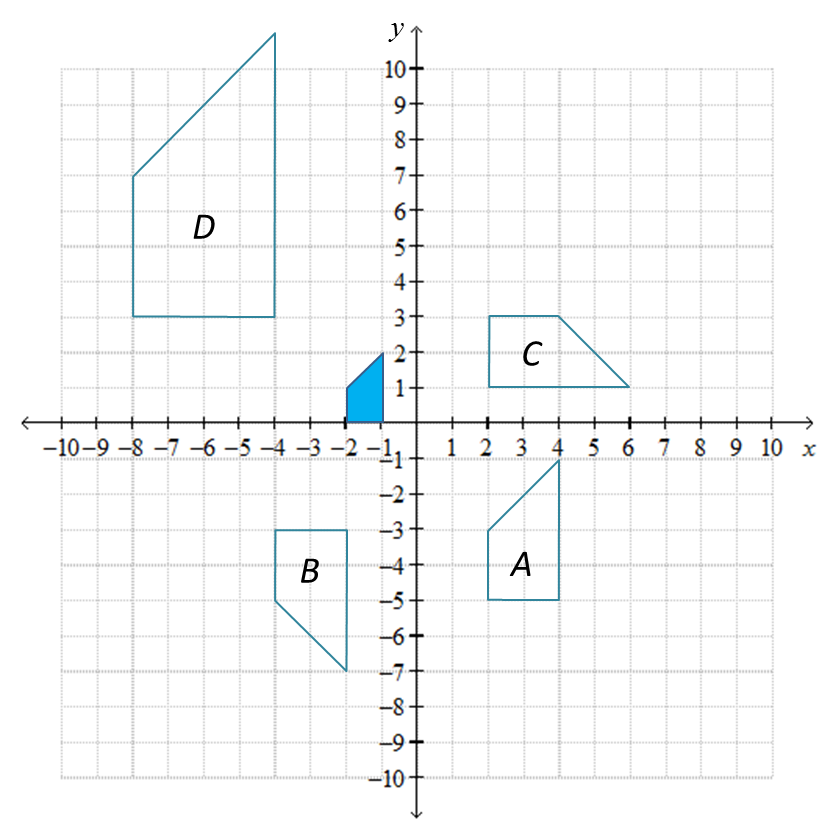
Cari koordinat-koordinat bagi imej titik A (3, –2) di bawah setiap gabungan penjelmaan berikut.
(a) TT
(b) PT
(c) ET
(d) ER
(e) EP
Penyelesaian:
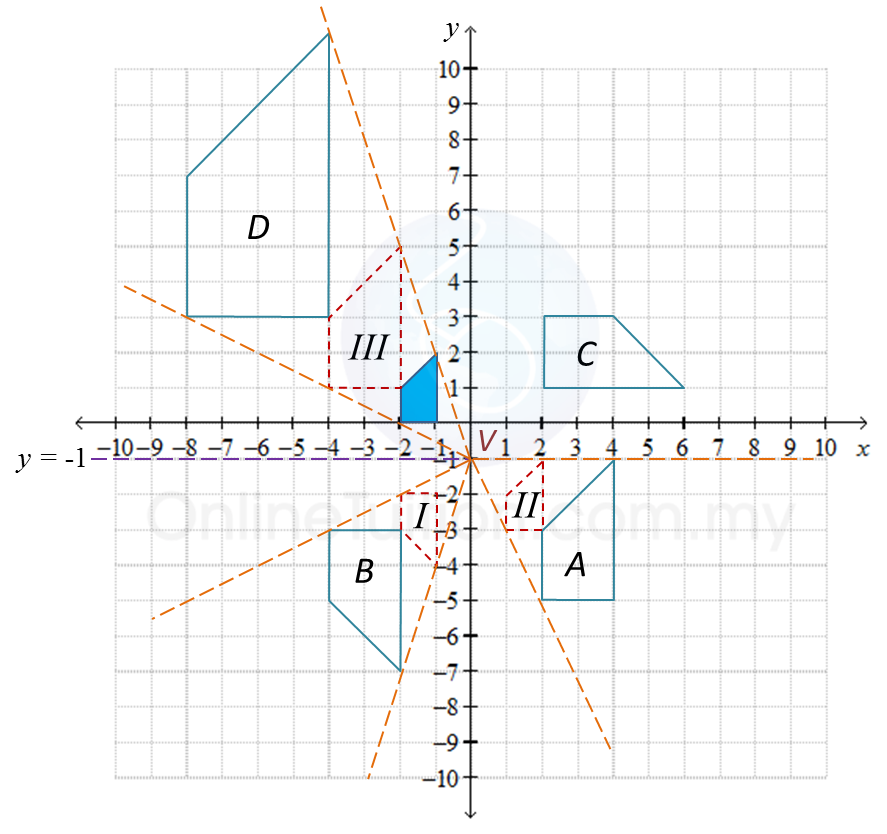
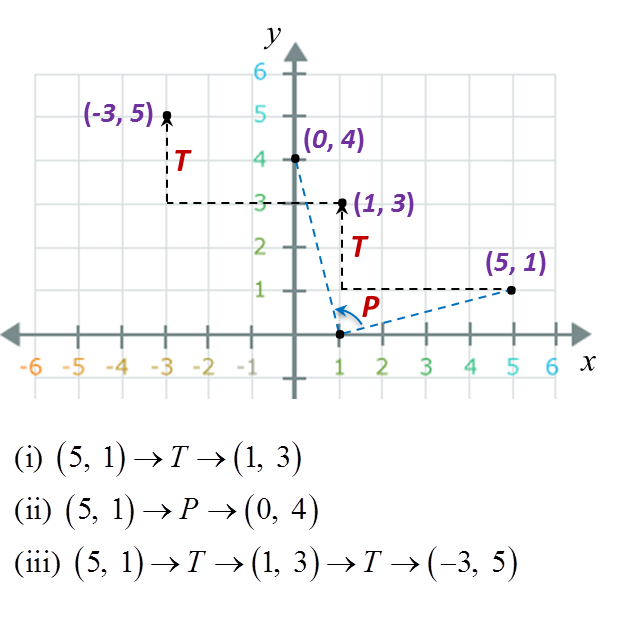
(a)
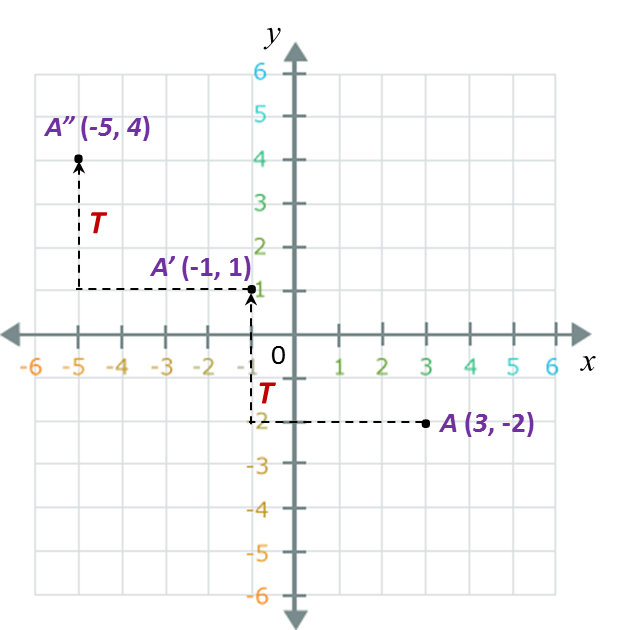
A(3, –2) → T → A’(–1, 1) → T → A”(–5, 4).
(b)
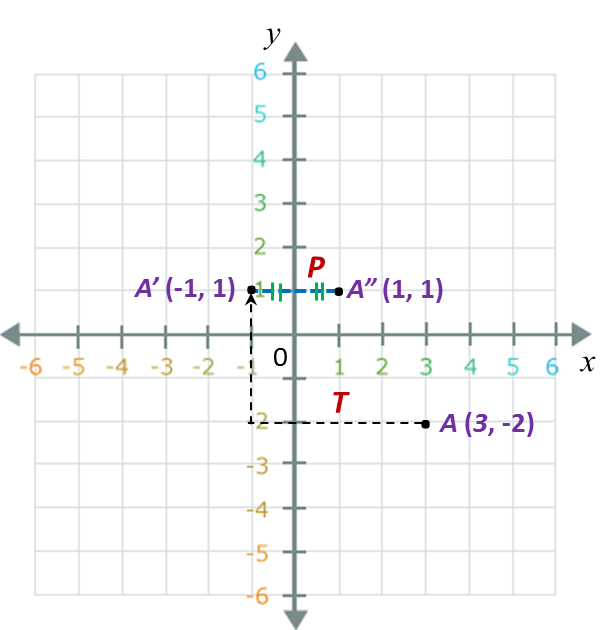
A(3, –2) → T → A’(–1, 1) → P → A”(1, 1).
(c)
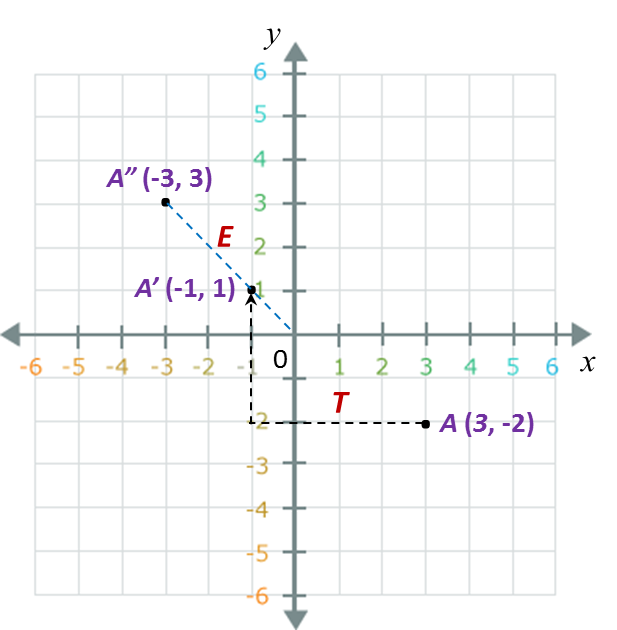
A(3, –2) → T → A’(–1, 1) → E → A”( –3, 3).
(d)
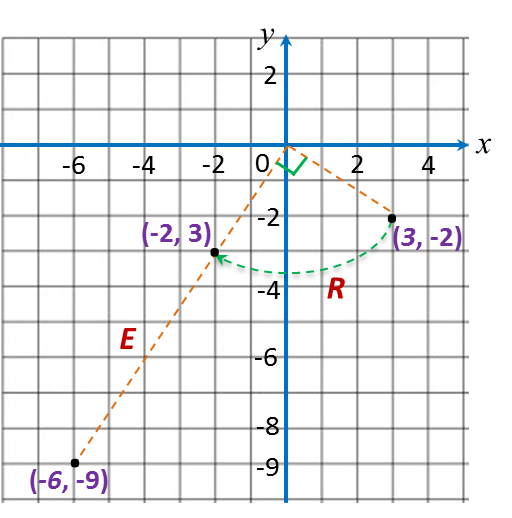
A(3, –2) → R → A’(–2, 3) → E → A”( –6, –9).
(e)
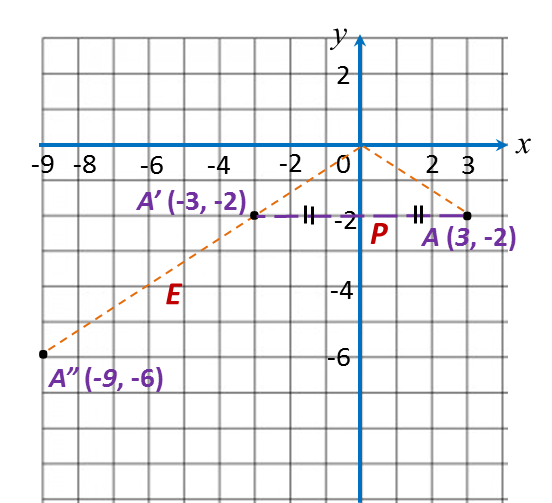
A(3, –2) → P → A’(–3, –2) → E → A”( –9, –6).